单选题
1/17
1.
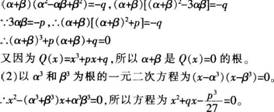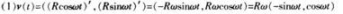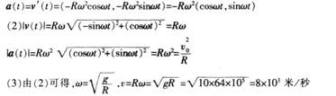
- A A
- B B
- C C
- D D
单选题
2/17
2.
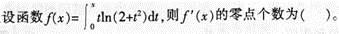
- A 0
- B 1
- C 2
- D 3
单选题
3/17
3.
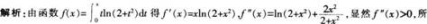
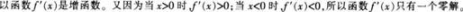
设M、N为随机事件，P(N)>0，且条件概率P(M|N)=1，则必有 
- A A
- B B
- C C
- D D
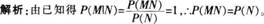P(MUN)=P(M)+P(N)-P(MN)，P(MUN)=P(M)。
单选题
6/17
6.
下列命题不正确的是( )。 
- A A
- B B
- C C
- D D
单选题
8/17
8.
- A χ2+z2=2py
- B χ2+y2=2pz
- C y2+z2=2pχ
- D χ2-y2=2pz
问答题
12/17
12.
若曲线y=χ4的一条切线I与直线χ+4y-8=0垂直，求切线I的方程。
问答题
13/17
13.
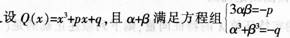(1)证明α+β是Q（χ）=0的根；(3分)
(2)写出以α3和β3为根的一元二次方程。(4分)
问答题
15/17
15.
设质点作匀速圆周运动，其轨迹为r (t)=(χ(t)，y(t))，其中χ(t)=Rcosωt，y(t)=Rsinωt，速度和加速度分别定义为v(t)=(χ′(t)，y′(t))，和a(t)=(χ"(t)，y" (t))。
(1)求v(t)和a(t)；(4分)
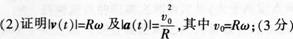
(3)若一飞行器绕地球作匀速圆周运动且只受重力作用(高度可忽略不计)，求其飞行速度的大小(设地球半径为6400千米，重力加速度为g=10米／秒2)。(3分)
问答题
16/17
16.
“数列”是高中数学必修5的内容。《普通高中数学课程标准(实验)》要求学生能“通过对日常生活中大量实际问题的分析，建立等差数列和等比数列这两种数列模型；在具体的问题情境中．发现数列的等差关系或等比关系，并能用有关知识解决相应的问题。”
(1)请设计一道能用等比数列知识解决的实际问题并求解；(20分)
(要求：给出问题情境；抽象出数量关系；建立数学模型；写出解答过程、讨论和反思。)
(2)根据上面的问题情境设计一道开放题或探索题。(10分)
问答题
17/17
17.
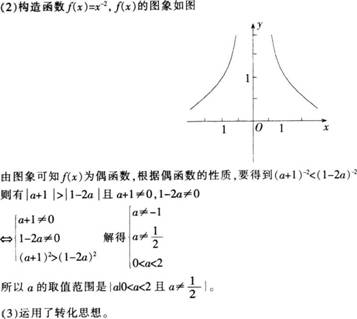
案例：某教师在进行幂函数教学时，给学生出了如下一道练习题：
已知(a+1)-2＜(1-2a)-2，求a的取值范围。
某学生的解答过程如下： 
问题：(1)指出该生解题过程中的错误，分析其错误原因；(8分)
(2)给出你的正确解答(限用幂函数的图像和性质来解答)；(8分)
(3)指出你解题所运用的数学思想方法。(4分)
