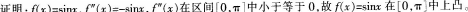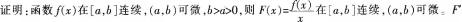有5个编号为1、2、3、4,5的红球和5个编号为1、2、3、4,5的黑球,从这10个球中取出4个,则取出的球的编号互不相同的概率为( )。
- A 5/21
- B 2/7
- C 1/3
- D 8/21
- 参考答案:D
- 您的答案:
参考解析:
把从l0个不同的球中取出4个球的组合看成基本事件,总方法数为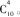 取出的4个球的编号互不相同的方法数,分两步:先确定选哪4个编号,确
取出的4个球的编号互不相同的方法数,分两步:先确定选哪4个编号,确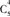 方法:再确定各编号球的颜色的方法有2x2x2x2=16种.即取出的4个球的编号互不相同的基本事件数为 因此.取出的4个球的编号互不相同的概率为
方法:再确定各编号球的颜色的方法有2x2x2x2=16种.即取出的4个球的编号互不相同的基本事件数为 因此.取出的4个球的编号互不相同的概率为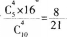 故选D,
故选D,
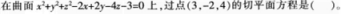
- A 2x-y+2z=0
- B 2x-y+2z=16
- C 4x-3y+6z=42
- D 4x-3y+6z=0
- 参考答案:B
- 您的答案:
参考解析:
方法一,设球面方程为x2.y2+z2+2px+2qr+2rz+d=0,则过球面上点(x。,y0)的切平面方程为: 
下面4个矩阵中,不是正交矩阵的是( )。
- A <img src='http://tp.mxqe.com/data/438/5386948_0.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题'>
- B <img src='http://tp.mxqe.com/data/438/5386948_0_1.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题'>
- C <img src='http://tp.mxqe.com/data/438/5386948_0_2.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题'>
- D <img src='http://tp.mxqe.com/data/438/5386948_0_3.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力初中真题'>
- 参考答案:C
- 您的答案:
参考解析:
A为n阶矩阵,
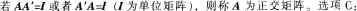
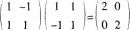 结果不是单位矩阵。故选C。
结果不是单位矩阵。故选C。
设{an}为数列,对于“存在正数肘,对任意正整数n,有
 的否定(即数列{an}无界)是( )。
的否定(即数列{an}无界)是( )。
- A 存在正数M,存在正整数n,使得|an|>M
- B 对任意正数M,存在正整数n,使得|an|>M
- C 存在正数M,对任意正整数n,有|an|>M
- D 对任意正数M以及任意正整数n,有|an|>M
- 参考答案:B
- 您的答案:
参考解析:
对任意正数M,存在正整数n,使得
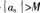 则称数列{an}无界.
则称数列{an}无界.
下列关于反证法的认识,错误的是( )。
- A 反证法是一种间接证明命题的方法
- B 反证法的逻辑依据之一是排中律
- C 反证法的逻辑依据之一是矛盾律
- D 反证法就是证明一个命题的逆否命题
- 参考答案:D
- 您的答案:
参考解析:
反证法是假设结论的反面成立,在已知条件和“否定结论”这个新条件下,通过逻辑推理,得出与公理、定理、题设、临时假定相矛盾的结论或自相矛盾,从而断定结论的反面不能成立,并不是证明它的逆否命题成立。
下列命题不是《义务教育数学课程标准(2011年版)》中规定的“图形与几何”领域的9条“基本事实”的是( )。
- A 两点之间线段最短
- B 过一点有且只有一条直线与这条直线垂直
- C 三边分别相等的两个三角形全等
- D 两条平行直线被第三条直线所截,同位角相等
- 参考答案:D
- 您的答案:
参考解析:
《义务教育数学课程标准(2011年版)》中规定的“图形与几何”领域的9条“基本事实”之一为“两条直线被第三条直线所截,如果同位角相等,那么两直线平行”。其余八条分别为:(1)两点确定一条直线;(2)两点之间线段最短;(3)过一点有且只有一条直线与这条直线垂直;(4)过直线外一点有且只有一条直线与已知直线平行;(5)两边及其夹角分别相等的两个三角形全等;(6)两角及其夹边分别相等的两三角形全等;
(7)三边分别相等的两个三角形全等;(8)两条直线被一组平行线所截,所得的对应线段成比例。
函数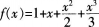 的图象与x轴交点的个数是( )。
的图象与x轴交点的个数是( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:B
- 您的答案:
参考解析:
 f(x)的图象与x轴有且只有一个交点。故选B。
f(x)的图象与x轴有且只有一个交点。故选B。
若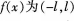 内的可导奇函数,则
内的可导奇函数,则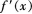 ( )。
( )。
- A 是(一1,1)内的偶函数
- B 是(一1,1)内的奇函数
- C 是(一1,1)内的非奇非偶函数
- D 可能是奇函数,也可能是偶函数
- 参考答案:A
- 您的答案:
参考解析:
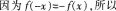
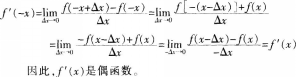
请以“变量(第一课时)”为课题,完成下列教学设计。
(1)教学目标。(5分)
(2)教学重点、难点。(4分)
(3)教学过程(只要求写出新课导入和新知探究、巩固、应用等)及设计意图。(21分)
对学生数学学习的评价,既要关注学习结果,也要关注学习过程,你认为对学生数学学习过程的评价应关注哪些方面?试举例说明。
- 参考答案:
- 您的答案:
参考解析:
本题主要考查的是对新课标的解读。
具体步骤: 1.把握题干,将题目涉及相关理论进行完善并完整论述; 2.举例阐述对学生数学学习过程的评价具体应该关注的方面。
求过点A(1,-2)的所有直线被圆x2+y2=5截得线段中点的轨迹方程。
- 参考答案:
- 您的答案:
参考解析:
占A存网卜.根据垂径定理可知.被圆截得线段中点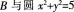 的圆心0(0,0)连线必然垂直于直线AB,所以B点在以0A为直径的圆上 (盲角所对的弦为直径)。所以B在以
的圆心0(0,0)连线必然垂直于直线AB,所以B点在以0A为直径的圆上 (盲角所对的弦为直径)。所以B在以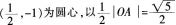 为半径的圆上。故B点的轨迹方程为
为半径的圆上。故B点的轨迹方程为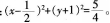
设P是3x3矩阵,其秩为2,考虑方程组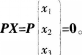
(1)设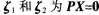 的两个解C1、C2为实数,证明
的两个解C1、C2为实数,证明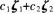 也是PX=0的解;(4分)
也是PX=0的解;(4分)
(2)方程组PX=0的解空间的维数是多少 (无需证明)(3分)
(1)叙述函数f(x)在区间a,b]中上凸的定义,并证明f(x)=sinx在[0,π]中上凸;(4分)
(2)若A、B、C为某三角形的三内角。证明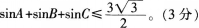
《义务教育数学课程标I隹(2011年版)》中“数据分析观念”的含义是什么
- 参考答案:
- 您的答案:
参考解析:
在新课程标准中,将数据分析观念解释为:了解在现实生活中有许多问题应当先做调查研究,收集数据,通过分析作出判断,体会数据中蕴涵着信息;了解对于同样的数据可以有多种分析的方法,需要根据问题的背景选择合适的方法;通过数据分析体验随机性,一方面对于同样的事情每次收集到的数据可能不同,另一方面只要有足够的数据就可能从中发现规律。数据分析是统计的核心。
如下图所示,设0<a<b,函数f(x)在[a,b]上连续,在(a,b)可微且f(x)>0,f(a)=f(b)。设f为绕原点0可转动的细棍(射线),放手后落在函数f(x)的图象上并支撑在点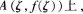 从直观上看.
从直观上看.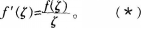 证明函数
证明函数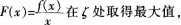 并由此证明(★)式。
并由此证明(★)式。
案例:阅读下列3个教师有关“代数式概念”的教学片段。
教师甲的情境创设:
“一隧道长Z米,一列火车长180米,如果该列火车穿过隧道所花的时间为t分钟.则列车的速度怎么表示 ”学生计算得出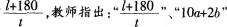 这类表达式称为代数式。
这类表达式称为代数式。
教师乙的教学过程:
复习上节内容后,教师在黑板上写下代数式的定义:“由运算符号、括号把数和字母连接而
成的表达式称为代数式”,特别指出“单独一个数或字母也称为代数式”;然后判断哪些是代数式.哪些不是;接着通过“由文字题列代数式”及“说出代数式所表示的意义”进一步解释代数式的概念:最后让学生练习与例题类似的题目。
教师丙的教学过程:
让学生自学教材,但是教材并没有说“代数式”是怎么来的,有什么作用。接着教师大胆地
提出开放式问题:“我们怎样用字母表示一个奇数 ”当时教室里静极了,学生们都在思考。
先有一位男生举手回答:“2a-1”。
“不对,若a=1.5呢 ”一位男生说。
沉默之后又有一位学生大声地说:“77,应该取整数!”
有些学生不大相信:“奇数77能用这个式子表示吗 ”
不久,许多学生算出来:“a取39”。
此时,教师趁势作了一个简单的点拔:“只要。取整数,2a-1一定是奇数,对吗 那么偶数呢 ”他并没有作更多的解说,点到为止,最后的课堂小结也很简单:“数和式有什么不同 ”“式中的字母有约束吗 ”“前面一节学过的式子很多都是代数式!……”从师生们自如的沟通来看,他们都已成竹在胸。
问题:
(1)你认可教师甲的情境创设吗 说明理由。(6分)
(2)你认可教师乙的教学过程吗 说明理由。(7分)
(3)你认可教师丙的教学过程吗 说明理由。(7分)
- 参考答案:
- 您的答案:
参考解析:
(1)甲教师情境创设的优点在于运用学生熟悉的物理背景来进行情境导入,降低了认知的难度。
缺点在于看似联系实际,其实脱离学生的现有认知水平,使学生的认知起点与数学逻辑起点失调,无法引起学生的思维共鸣,使问题情境中隐含的数学问题与数学方法不能与教学目标相衔接,不能形成学生原有认知水平及生活经验的正迁移。
(2)乙教师的教学过程存在优点也存在缺陷。优点是一开始复习了上节内容,进行了薪旧知识间的过渡,降低了学生对新知识的认知难度;采取了直接导入的方法,开门见山的介绍本节课题,引起学生的注意,使学生迅速进入学习状态,对本节内容的基本轮廓有了大致了解;整个教学过程条理清楚、重难点突出;最后进行巩固练习,加深了学生对新知识的识记和掌握。
缺点在于没有进行合适的情境创设,将知识全盘塞给学生,剥夺了学生研究问题的权利,无法激发学生学习新知识的兴趣,学生只能机械地配合老师的教学,整个过程中,缺乏师生问的互动,忽了学生的主体地位。
(3)丙教师的教学过程存在优点也存在缺陷。优点是充分发挥了学生的主体地位,开放性问题激发了学生自主探究的兴趣,有利于培养他们的独立思考能力和创新意识。
缺点在于首先教师没有给出学生自主探究的准备时间,没有提供丰富的自学素材;另外教师导入的开放式
问题并不能充分突出代数式这节的核心“数”与“式”的区别;在探究过程中,教师没有科学合理地发挥自己的主导作用,小结也显得过于潦草和模糊。
 (2)方程组PX=0的解空间的维数是未知量的个数n=3减去系数矩阵P的秩2,即为1。
(2)方程组PX=0的解空间的维数是未知量的个数n=3减去系数矩阵P的秩2,即为1。