在高等代数中,有一种线性变换叫做正交变换,即不改变任意两点的距离的变换。下列变换中不是正交变换的是( )。
- A 平移变换
- B 旋转变换
- C 反射变换
- D 相似变换’
- 参考答案:D
- 您的答案:
参考解析:
相似变换改变两点之间的距离,其余三种变换都不改变任意两点问的距离。
《普通高中数学课程标准(实验)》中规定的必修课程是每个学生都必须学习的数学内容,列内容不属于必修4的是( )。
- A 算法初步
- B 基本初等函数Ⅱ(三角函数)
- C 平面上的向量
- D 三角恒等变换
- 参考答案:A
- 您的答案:
参考解析:
基本初等函数II(三角函数)、平面上的向量、三角恒等变换都属于必修4的内容,算法初步是选修3的内容之一,故选A。
8个同学排成一排的排列数为m,8个同学排成前后两排,其中前排3人,后排5人的排列数为n,则m、n的关系是( )。
- A n<m<2n
- B m<n
- C m>n
- D m=n
- 参考答案:D
- 您的答案:
参考解析:
对于排成前后两排(前排3人,后排5人)可以理解成8个同学排成一排后将5个人移到后排.和排成一排的排列数相同。
下列说法正确的是( )。
- A 四边相等的四边形必是平面图形
- B 梯形一定是平面图形
- C 不平行的两条直线一定相交
- D 没有公共点的两条直线是平行线
- 参考答案:B
- 您的答案:
参考解析:
A不正确,也可能是立体图形;B正确,梯形是平面图形;c、D都不正确,不平行的两条直线和没有交点的两条直线都可能异面。
《普通高中数学课程标准(实验)》中规定必修课程是每个学生都必须学习的数学内容,列内容不属于必修4的是( )。
- A 算法初步
- B 基本初等函数Ⅱ(三角函数)
- C 平面上的向量
- D 三角恒等变换
- 参考答案:A
- 您的答案:
参考解析:
基本初等函数II(三角函数)、平面上的向量、三角恒等变换都属于必修4的内容,算法初步是选修3的内容之一,故选A。
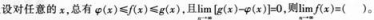
- A 存在且等于零
- B 存在但不一定为零
- C 一定不存在
- D 不一定存在
- 参考答案:D
- 您的答案:
参考解析:
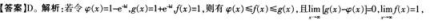
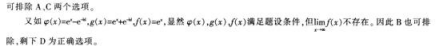
经过点(2,-3,-5)且与平面6x-3y-5z+2=0垂直的直线为( )。 
- A A
- B B
- C C
- D D
- 参考答案:A
- 您的答案:
参考解析:
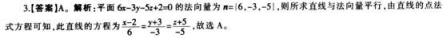
( )是学生在教师的指导或鼓励下,通过类比、归纳、质疑和反思等思维活动.亲自去探索和发现数学的概念、定理、公式和解题方法等的一种教学方法。
- A 发现式教学法
- B 讲解式教学法
- C 自学辅导法
- D 讨论式教学法
- 参考答案:A
- 您的答案:
参考解析:
题干给出的是发现式教学法的定义,故选A。
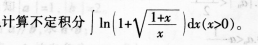
- 参考答案:
- 您的答案:
参考解析:

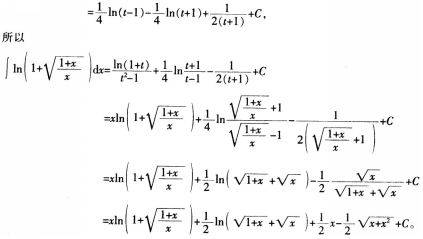
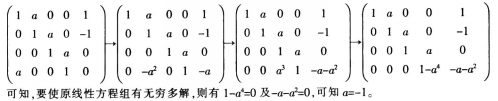
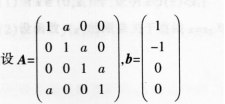 (1)求|A|;
(1)求|A|;
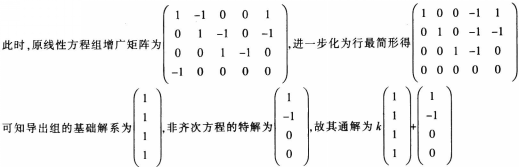
(2)已知线性方程组AX=b有无穷多解,求a,并求A=b的通解。
- 参考答案:
- 您的答案:
参考解析:
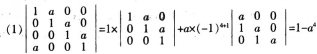
李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立): 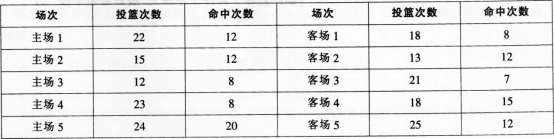
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率。
(2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率。
- 参考答案:
- 您的答案:
参考解析:
(1)根据投篮统计数据,在10场比赛中,李明投篮命中率超过0.6的场次有5场,分别是主场2,主场3,主场5,客场2,客场4。
所以在随机选择的一场比赛中,李明的投篮命中率超过0.6的概率是0.5。
(2)设事件A为“在随机选择的一场主场比赛中李明的投篮命中率超过0.6”,
事件B为“在随机选择的一场客场比赛中李明的投篮命中率超过0.6”,
事件C为“在随机选择的一个主场和一个客场中,李明的投篮命中率一场超过0.6,一场不超过0.6”,

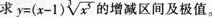
- 参考答案:
- 您的答案:
参考解析:

袋中有l个红色球,2个黑色球与三个白球,现有放回地从袋中取两次,每次取一球,以 X,Y,Z分别表示丽次取球所取得的红球、黑球与白球的个数。
(1)求P{X=1|Z=0};
(2)求二维随机变量(X,Y)的概率分布。
- 参考答案:
- 您的答案:
参考解析:

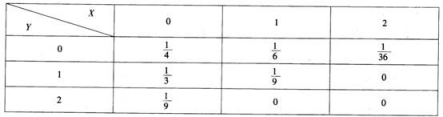
设F(χ)=f(χ)g(χ),其中函数f(χ),g(χ)在(-∞,+∞)内满足以下条件: f’(χ)=g(χ),g’(χ)=f(χ),且f(0)=0,f(χ)+g(χ)=2eχ。 (1)求F(χ)所满足的一阶微分方程; (2)求出F(χ)的表达式。
- 参考答案:
- 您的答案:
参考解析:


简要论述自主学习与自学的区别。
- 参考答案:
- 您的答案:
参考解析:
第一,自主学习是在教学条件下进行的,而且在目前情况下,主要是在班级中发生的;而自学是一种与教学条件下的学习相对的学习方式(至少在它出现之初如此)。第二,自主学习的动机是内在的或自我激发的,即自主学习是源于自我目标、自我价值等的驱动而展开的。第三,自主学习者的学习方法是有计划的或已经熟练到自动化的程度。第四,自主学习的时间是定时而有效的。第五,自主学习都对学习结果有较强的自我意识。第六,自主学习者对物质环境很敏感,所以他们能根据需要随机应变地选择或组织自己的学习环境。第七,自主学习者可以随时向教师或同学寻求帮助。
案例:
概念同化指从已有概念出发,理解并接纳新概念的过程,实质是利用演绎方式理解和掌握概念。由于数学中大多数概念是以属概念加种差的方式定义的,所以适宜采用概念同化的方式进行教学。以“奇函数,,概念教学为例简要说明概念同化的教学模式:
(1)向学生提供“奇函数”概念的定义
(2)解释定义中的词语、符号、式子所代表的含义
突出概念刻画的是:对定义域中的任意一个自变量菇,考察χ与-χ对应的函数值f(χ)与f(-χ)之间的关系以f(-χ)=-f(χ)。因此函数的定义域应该关于原点对称,满足这个条件后再考察f(-χ)=-f(χ).
(3)辨别例证,深化概念
教师向学生提供丰富的概念例证,例证中以正例为主,但也要包合适"-3的反例,尤其是一些需要考察隐含条件的例子。
(4)概念的运用
提供各种形式来运用概念,达到强化对概念的理解,促进概念体系的建构的目的,可以利用个别有一定综合性但难度不大的问题。
问题:(1)请举出反例说明(3)辨别例证,深化概念。(5分)
(2)请举例补充(4)概念的运用。(5分)
(3)请结合案例,总结出概念同化的教学模式的过程。(10分)
- 参考答案:
- 您的答案:
参考解析:
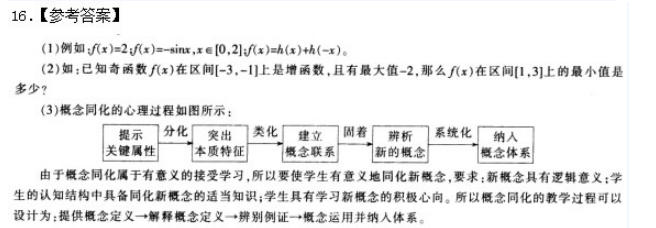
下面是某教师执教《不等式的运用》的教学过程。
教学的具体环节如下: 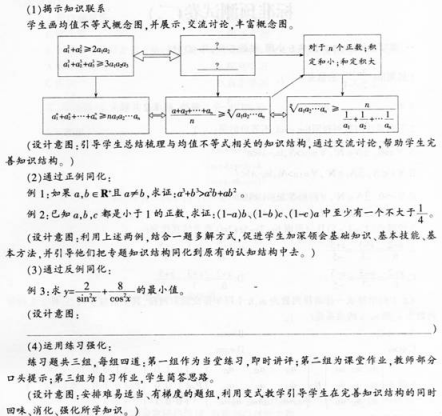
请完成下列任务:
(1)请完成概念图中问号处的不等式;(6分)
(2)请补充完例3通过反例同化的设计意图;(6分)
(3)关于《不等式的运用》的教学过程,给出你的教学目标设计;(8分)
(4)请对上述这位教师执教《不等式的运用》的教学过程作出评价。(10分)
- 参考答案:
- 您的答案:
参考解析:
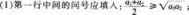
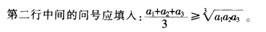 (2)例3的设计意图:通过例3剖析错解、引出正确的教学策,把学生置于原有认知结构与新问题矛盾的冲突之中,引导他们顺应新问题、新体会,调整原有认知结构从而达到新平衡。
(2)例3的设计意图:通过例3剖析错解、引出正确的教学策,把学生置于原有认知结构与新问题矛盾的冲突之中,引导他们顺应新问题、新体会,调整原有认知结构从而达到新平衡。
(3)知识与技能目标:掌握均值不等式,能根据问题条件的需要灵活运用均值不等式解决相关问题。
过程与方法目标:通过相关知识的梳理,以及正例同化与反例顺应,优化认知结构,进一步发展恒等变形与转化化归的能力,发展思维的灵活性与创新性。
情感态度与价值观目标:经历知识的系统化过程,感受数学知识的内在联系,领悟数学知识的生长规律;经历师生、生生交流、合作与探究、批判与反思,增进理性思维的发展,并获得成功的体验。
(4)上述教学过程,基本符合教学要求、学生实际,反映了新课程的基本理念。而且,教学过程设计比较具体,可操作性强,能保证教学目标的实现。但有两个环节不容易把握:一是对知识结构梳理;二是利用反例顺应。这两个环节也是引导学生进行高水平认知活动的重要环节,对于学生的不同想法,教师应只引申和明确,不能限制学生的思路,要给教学的动态生成以充分的空间和时间。
