设函数f(χ)=(eχ-1)(e2χ-2)…(enχ-n),其中n为正整数,则f’(O)=( )。
- A (-1)n-1(n-1)!
- B (-1)n(n-1)!
- C (-1)n-1n!
- D (-1)nn!
- 参考答案:A
- 您的答案:
参考解析:
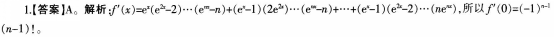
牛顿和( )创立的微积分开创了数学的新领域:分析学。微积分将以难以解决的两个几何问题(曲线切线问题和曲线所围面积问题)解决了,把这些问题简化为计算问题。
- A 笛卡尔
- B 莱布尼茨
- C 费马
- D 欧拉
- 参考答案:B
- 您的答案:
参考解析:

已知曲面方程为χ2+y2+z2-2χ+8y+6z=10,则过点(5,-2,1)的切平面方程为( )。
- A 2χ+y+2z=0
- B 2χ+y+2z=10
- C χ-2y+6z=15
- D χ-2y+6z=0
- 参考答案:B
- 您的答案:
参考解析:
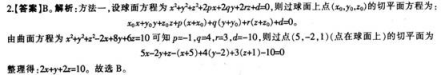

设函数f(χ)在(-∞,+∞)内连续,其中二阶导数f”(χ)的图形如图所示,则曲线y=f(χ)的拐点的个数为( )。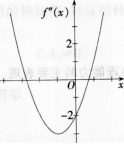
- A 0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:
拐点出现在二阶导数等于零,或二阶导数不存在的数,并且在这点的左右两侧二阶导函数异号。因此,由f〞(x)的图形可得,曲线y=f(x)存在两个拐点。
设函数f(x)在(-∞,+∞)内连续,其中二阶导数f”(χ)的图形如图所示,则曲线y=f(χ)的拐点的个数为( )。 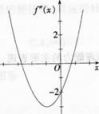
- A 0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:
拐点出现在二阶导数等于零,或二阶导数不存在的数,并且在这点的左右两侧二阶导函数异号。因此,由f〞(x)的图形可得,曲线y=f(x)存在两个拐点。
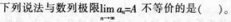
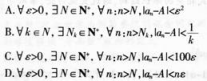
- A A
- B B
- C C
- D D
- 参考答案:D
- 您的答案:
参考解析:
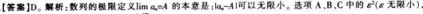
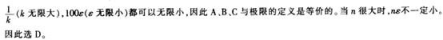
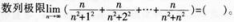
- A π/2
- B π/4
- C π/3
- D π/6
- 参考答案:B
- 您的答案:
参考解析:




- A a=b或a+2b-0
- B a=b或a+2b≠0
- C a≠b且a+2b-0
- D a≠b且a+2b≠0
- 参考答案:C
- 您的答案:
参考解析:

给出中学几何研究图形的几个主要方法,并试以其中一种为例,说明该种方法的基本特点。
- 参考答案:
- 您的答案:
参考解析:
中学几何研究图形的方法主要有:综合几何的方法,解析几何的方法,向量几何的方法,函数的方法等。
综合几何的方法是利用几何的方法研究图形的性质,即用已知的基本图形的性质去研究组合图形的性质。这种方法的基本特点就是把复杂的图形转化为简单的图形,把空间的图形转化为平面图形。例如,把两条线段相等问题转化为两个三角形全等关系或一个三角形内两边的相等关系,空间两直线的垂直问题转化为平面两直线垂直(如三垂线定理),利用三视图研究空间几何体等。在综合几何方法中,平移、旋转、对称等是研究综合图形性质的基本方法。
计算二重积分
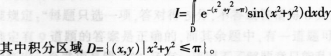
- 参考答案:
- 您的答案:
参考解析:
从被积函数与积分区域可以看出,应利用极坐标进行计算。
作极坐标变换:设x=rcosθ,y=rsinθ,有
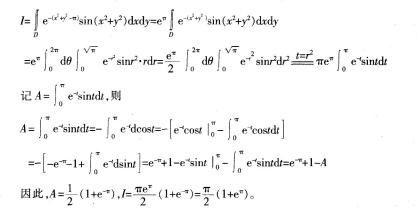
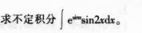
- 参考答案:
- 您的答案:
参考解析:
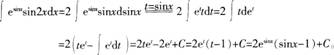
强调数据处理能力是高中数学课程的一个变化,有人说统计的概念不难掌握,请谈谈在
教学中应如何看待统计概念的定义。
- 参考答案:
- 您的答案:
参考解析:
高中统计的学习,本质上是统计活动的学习,而不是概念和公式的学习。统计内容的教学不应该单纯地讲授概念的定义,图表的制作,数字特征的计算,机械地套用公式。而应该从提取信息的角度比较各种方法的优劣,了解它们的适用范围,让学生通过对实际问题的解决来理解统计的思想,而不是死背公式和定义。
(1)关注三种抽样方法的差别和不同的实用范围;
(2)应侧重于了解统计图表能告诉我们何种信息和理解不同统计图表的特点;
(3)让学生了解数据的数字特征的作用和意义。
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:





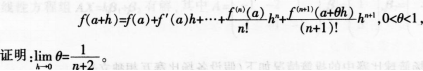
- 参考答案:
- 您的答案:
参考解析:

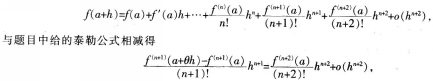
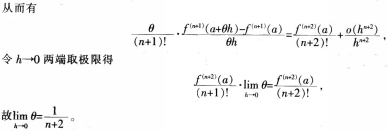
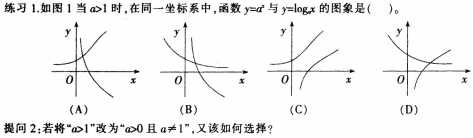
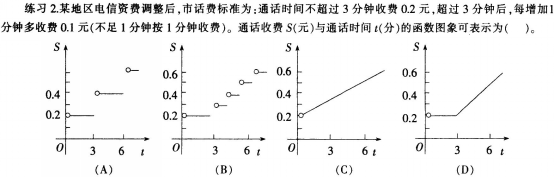
“函数图象”是高中数学中很重要的知识点,通过复习所学函数模型及其图象特征.可以使学生对函数有一个较直观的把握和较形象的理解,缓解因函数语言的抽象性引起的学生的心理不适应及不自觉的排斥情绪。
(1)关于“函数图象及其应用”给出你的教学设计目标。(10分)
(2)确定教学重点、难点。(10分)
(3)设置两个教学环节(给出两个以上例题或练习题)并说明设计意图。(10分)
- 参考答案:
- 您的答案:
参考解析:
(1)教学目标主要有:
①通过练习的设置,从解决简单实际问题的过程中,体会函数模型的广泛适用性,贯穿理论联系实际、学以致用的观点,充分体现数学的应用价值,加强看图识图能力,激发学习兴趣,自觉自主参与课堂教学活动。②结合具体的问题,并从特殊推广到一般,领会函数与方程之间的内在联系,体验函数与方程思想、数形结合思想及等价转化思想的意义和价值。③通过对所给问题的自主探究和合作交流,理解动与静,整体与局部的辨证统一关系,发展对变量数学的认识,体会函数知识的核心作用。
(2)教学重点和难点
①教学重点:常见函数模型的图象特征和实际应用。通过课堂师生互动交流。共同完成对相关知识的系统归纳,借助多媒体课件演示,增加学生的直观体验,深化认识,突破重点。
②教学难点:利用函数图象研究方程问题的思想和方法。在教学过程中,自主探究学习,在实际问题的解决中学习将抽象的数学语言与直观的图象结合起来,充分利用这种结合,寻找解题思路,使问题化难为易、化繁为简,实现难点突破。
(3)教学环节及设计意图
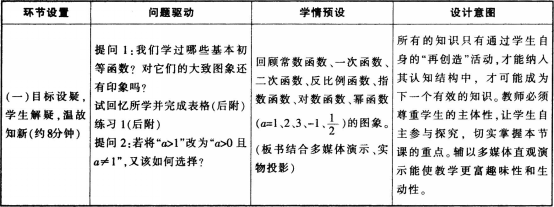






课堂小结:
本节课复习了常见函数模型及其图象特征,体会到利用函数图象解决函数性质的形象和直观。学习函数和方程的相互等价转化,体会函数方程思想与数形结合思想的意义和价值。
正如华罗庚所说:数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休。
案例:阅读下列两位教师的教学过程。教师甲的教学过程:
师:在一个风雨交加的夜里.从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10 km长的线路,如何迅速查出故障所在
如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次10 m长的电线杆子,大 约有200多根电线杆子呢。想一想,维修线路的工人师傅怎样工作最合理
生1:直接一个个电线杆去寻找。
生2:先找中点,缩小范围.再找剩下来一半的中点。师:生2的方法是不是对呢 我们一起来考虑一下。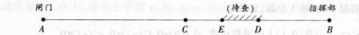
如图,维修工人首先从中点C查,用随身带的话机向两个端点测试时,发现A C段正常,断 定故障在BC段,再到BC段中点D,这次发现BD段正常,可见故障在CD段,再到CD中点E 来查。每查一次,可以把待查的线路长度缩减一半,如此查下去.不用几次,就能把故障点锁定 在一两根电线杆附近。
师:我们可以用一个动态过程来展示一下(展示多媒体课件)。
在一条线段上找某个特定点,可以通过取中点的方法逐步缩小特定点所在的范围(即二分 法思想)。
教师乙的教学过程:
师:大家都看过李咏主持的《幸运52》吧,今天咱也试一回(出示游戏:看商品、猜价格)。
生:积极参与游戏.课堂气氛活跃。
师:竞猜中,“高了”“低了”的含义是什么 如何确定价格的最可能的范围
生:主持人“高了、低了”的回答是判断价格所在区间的依据。
师:如何才能更快的猜中商品的预定价格
生:回答各异。
老师由此引导学生说出“二分法”的思想,并向同学们引出二分法的概念。
问题:
(1)分析两种情境引入的特点。(10分)
(2)结合案例,说明为什么要学习用二分法求方程的近似解。(10分)
- 参考答案:
- 您的答案:
参考解析:
(1)甲教师从实际问题入手,利用计算机演示用二分法思想查找故障发生点。通过演示初步体会二分法的算法思想与方法,说明二分法原理源于现实生活,并在现实生活中广泛应用。
乙教师利用视频与游戏的形式,学生会踊跃参与;商品价格竞猜也是学生熟悉的,竞猜的方法多样,可以进行竞赛;通过问题,启发学生寻找确定区间的依据,为后面探索“用二分法求方程近似解”埋下伏笔。
(2)首先,新课程标准强调函数的应用,用二分法求方程的近似解体现了函数在数学其他方面的应用。概括来说,函数应用表现在两个方面,一是在数学其他方面的应用;二是在其他科学领域和实际向题中的应用。
其次,二分法简便而又应用广泛,用在求方程的近似解方面是依据了方程解存在的重要结论。即函数的应用。二分法求方程的解这一内容也是函数思想存在的一个良好载体。
二分法还是数学必修3中算法学习的一个铺垫。在教学中可以用框图表示二分法求方程近似解的流程。
再次,二分法朴素地体现了数学逼近的过程,二分法虽然简单,但包含了许多以后可以在其他地方运用和推广的朴素的思想,如“整体→局部”“定性→定量”“精确→近似”“计算→技术”等。这些数学思想发展的过程,具有萌发数学思想的数学教育价值。
