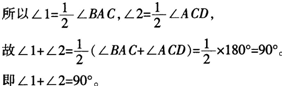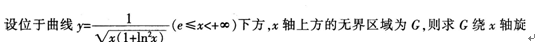已知f(x),g(x)分别是定义在R上的偶函数和奇函数,且f(x)一g(x)=X3+x2+1,则f(1)+g(1)=( )。
- A -3
- B -1
- C 1
- D 3
- 参考答案:C
- 您的答案:
参考解析:
令X=﹣1,可得f(一1)-g(一1)=1,又由于f(x),g(x)分别是定义在R上的偶函数和奇函数,即f(一l) =f(1),g(-1)=g(1),则f(一1) -g(1) =f( 1) +g(1)=1,所以答案为C。
设A为3阶矩阵,将A的第2列加到第l列得矩阵曰,再将曰的第2行与第3行交换得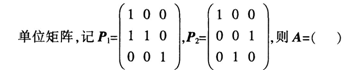
- A P1p2
- B P-11 P2
- C P2P1
- D P2P一11
- 参考答案:C
- 您的答案:
参考解析:
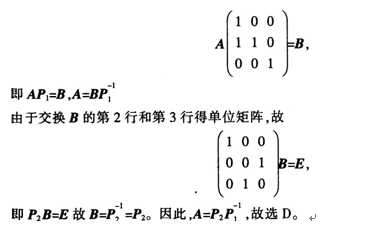
由于将A的第2列加到第l列得矩阵曰,
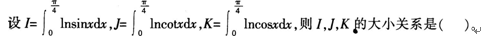
- A I<J<K
- B I<K<J
- C J<I<K
- D K<J<I
- 参考答案:B
- 您的答案:
参考解析:

下列不属于初中数学课程知识技能目标的是( )。
- A 探索并掌握相交线、平行线、三角形、四边形和圆的基本性质与判定
- B 体验数据收集、处理、分析和推理过程
- C 积极参与数学活动。对数学有好奇心和求知欲
- D 探索具体问题中的数量关系和变化规律
- 参考答案:C
- 您的答案:
参考解析:
C选项属于情感态度方面的目标,其他都属于知识技能方面的目标。
几何学巨著《几何原本》一书的作者是哪位著名的数学家 ( )
- A 欧几里得
- B 惠更斯
- C 欧拉
- D 海亚姆
- 参考答案:A
- 您的答案:
参考解析:
略


- A A
- B B
- C C
- D D
- 参考答案:B
- 您的答案:
参考解析:
已知向量a=(k,3),b=(1,4),c=(2,1),R(2a一3b)上c,则实数k=( )。
- A -4.5
- B 0
- C 3
- D 5.5
- 参考答案:C
- 您的答案:
参考解析:
∵2a一3b⊥c,∴(2a一3b)c=0,即2ac=3bc,即2(2k+3)=3(2+4),解得k=3。所以答案选择C。
教学方法的使用对教学效果非常重要,教学方法的使用一定要灵活,不能僵化、教条。选择教学方法总的原则是启发式:“不愤不启,不悱不发。”请简述选择教学方法时需要考虑哪些问题?
- 参考答案:
- 您的答案:
参考解析:
(1)教学方法的选择要考虑初中阶段的课程目标:(2)教学方法的选择要考虑教学内容的特点; (3)教学方法的选择要考虑教学条件;
(4)教学方法的选择要考虑学生的实际情况;..
(5)教学方法的选择要考虑教学方法的特点,将各种教学方法进行有机结合。
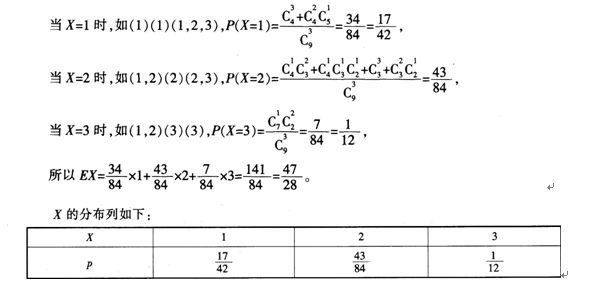
一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是l,3张卡片上的数
字是2,2张卡片上的数字是3,从盒中任取3张卡片。(1)求所取3张卡片上的数字完全相同的概率;(2)x表示所取3张卡片上的数字的中位数,求X的分布列和EX。
设向量组α1=(1,0,1)T,α2=(0,1,1)T,a3=(1,3,5)T,不能由向量组β1,=(1,1,1)T,f12=(1,2,3)T,3β=(3,4,α)T线性表示。
(1)求a的值;
(2)将β1β2β2由α1α2α3线性表示。
- 参考答案:
- 您的答案:
参考解析:
(1)由于α1,α2,α3不能由β1β2β3,线性表示,对(β1,β2,β3,α1,α2,α3进行初等变换∶

故β1=2α1+4α2-α3,β2=α1+2α2,β3=5α1+10α2-2α3
《义务教育课程数学课程标准(2011年版)》中强调培养学生的“数感”。简述数感的含义及建立数感有哪些意义?

- 参考答案:
- 您的答案:
参考解析:

点η∈(0,2),使得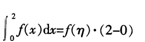 即2f(o)=2f(η),所以存在η∈(0,2),使得发f(η) =(0)。
即2f(o)=2f(η),所以存在η∈(0,2),使得发f(η) =(0)。
(Ⅱ) 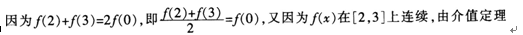
知,至少存在一点。∈(2,3)使得f(η1=f(0)。
因为.厂(x)在[0,2]上连续,在[0,2]上可导,且f(0)f(2),所以由罗尔中值定理知,存在ξ1∈(0,2),有f'(ξ1)=0。
又因为.厂(x)在[2,η1],]上连续,在(2,η1)上可导,且f(2)=f(0)=f(η1),所以由罗尔中值定理知,存在ξ∈(2,η1),有f'(ξ2)=0。
又因为f(x)在[ξ1,ξ2]上二阶可导,且f'(ξ1)='(ξ2)=0,所以由罗尔中值定理,至少有一点∈(ξ1,ξ2)c(0,3),使得f”(ξ) =0。
我国数学教育界历来重视中学数学概念的教学,对概念教学活动的认识主要有哪几种倾向?对数学概念教学的认识与提高应注意哪些问题?
- 参考答案:
- 您的答案:
参考解析:
(1)①在概念教学中过分重视定义的叙述,对定义字字推敲,处处斟酌,不厌其烦地举正、反例,并且要求学生熟读定义,熟记定义。这种教育往往是费时费力,但效果欠佳。其主要缺点是:a.容易将学生导向只注意死记硬背定义和结论,而不求深入地理解概念;b.由于学生思维中缺少能说明概念关键特征的具体形象,一旦不能用已有的模式解决问题,就会感到束手无策,因此不利于数学思维能力的提高。 ②在概念教学中,不注意概念的引人,只重概念的应用,引入概念的过程过于简单,对定义的表述一掠而过。匆忙转入练习,这样做的缺点在于:a.学生对概念缺乏从感性到理性的认识,只注意掌握一些题型与具体的解题技能,难以形成数学能力。b.由于新概念的引入没能以学生原有的认知结构为基础。又没能通过大量实例揭露概念的关键特征,因此新概念不能较好地纳入认知结构中,缺乏系统化,记忆也难以长期保持。
(2)①重视解释概念的内涵与外延,重视概念学习之间的迁移影响
数学概念具有确定的内涵与外延.教学的迁移要重视深入揭示概念的外延,把新旧概念的由来和发展、区别和联系进行剖析、类比,深刻理解、灵活运用、克服负迁移、发挥正迁移。
②数学概念教学是素质教育的重要内容
复习旧课,讲授新课,离不开概念,在现代教学的发展中,概念教学不仅不能削弱,而且要更自觉、更有意识、更科学地进行。
③数学概念教学是~个完整的教学过程,不可有头无尾
有的教师误认为只要引入定义.举几个例子就算是完成了概念教学的任务,还有一些文章
、错误地认为“定义”就是“概念”。实际上,定义只是概念本质属性的一种表达形式。单纯在定义身上下工夫,在讲定义处停留过久是不妥当的。数学概念教学是一个过程,这个过程大致可以分为四个阶段:概括、表述、识别和运用。
④数学概念教学要抓住关键,不可追求单一的教学模式
如果教师讲授每个数学概念都从具体出发,进行抽象概括,是不符合数学教学实际的,其中的关键问题,是教师要明确影响概念学习的因素。影响概念学习的因素有以下几点:学生的年龄、经验与智力,感性材料或感性经验方面,学生的概括能力,学生的语言表达能力。
⑤要在数学思想、方法的高度上进行数学概念教学
数学概念和其他数学知识一样,是中学数学的表层知识,而数学思想、方法是数学的深层知识,深层知识蕴含于表层知识中,是表层知识的本质,是分析、处理和解决数学问题的策略和基本方法。因此,数学概念教学的主要目标之一是使学生通过概念的掌握和应用.最终理解和掌握数学思想、方法。只有当学生在数学思想、方法的高度上掌握数学概念、数学知识时,才能较好地形成数学能力,受益终生。
阅读案例。并回答问题案例:
下面是“等腰三角形”教学片段的描述,阅读并回答问题:片段一:请同学们把一张长方形的纸片对折,剪去(或用刀子裁)一个角,再把它展开。得到
的是什么样三角形? ? ?‘
? ? 教师示范操作,然后学生跟着动手操作,观察得出结论:‘‘剪刀剪过的两条边是相等的:剪出的图形是等腰三角形”,根据学生回答,板书:等腰三角形。
? ? 师生共同回顾:有两条边相等的三角形,叫做等腰三角形,相等的两边叫做腰,另一条边叫做底,两腰所夹的角叫做顶角,底边与腰的夹角叫做底角。
? ? 教师提问:剪出的三角形是轴对称图形吗?你能发现这个三角形有哪些特点吗?说一说你的猜想。
? ? 学生思考并发表自己的看法,教师提出本节课所要解决的问题。
? ? 师生归纳:等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴。(板书)教师说明:对称轴是一条直线,而三角形的中线是线段,因此不能说等腰三角形底边上的中线是它的对称轴。
? ? 片段二:教师出示刚才剪下的等腰三角形纸片.标上字母如图所示.

片段三:由上面的性质我们可以得到等腰三角形如下性质:
? 性质l:等腰三角形的两个底角相等,简称:等边对等角。(板书)(证明过程略)。
? 教师提出问题:练习(略)
? 要求学生完成教师提出的问题,教师归纳:
? (1)等腰三角形中顶角与底角的关系:顶角+2x底角=180。
(2)推论:等边三角形三个内角相等.每一个内角都等于600。(板书)

让学生运用数学语言表述所发现的规律,师生共同归纳得出:性质2:等腰三角形的顶角的平分线垂直平分底边。(板书)即:等腰三角形顶角的平分线、底边上的中线和底边上的高互相重合,三线合一。(板书)
? 教师出示课本例题供学生练习。问题:
? (1)请确定这四个片段的整体教学目标;
? (2)请根据片段三中教师归纳出的结论设计至少5个练习题;
?(3)这四个片段对数学课堂教学有哪些启示?
- 参考答案:
- 您的答案:
参考解析:
(1)知识与能力目标: ①掌握等腰三角形的性质及其推论。
②运用等腰三角形的性质及其推论进行有关证明和计算。过程与方法目标:
①让学生体验等腰三角形是一个轴对称性图形。
②经历操作、发现、猜想、证明的过程,培养学生的逻辑思维能力。情感、态度、价值观目标:
培养学生协作学习精神,使学生理解事物之间是相互联系和运动变化的,培养学生辩证唯物主义观念。
(2)①等腰直角三角形每一个锐角的度数是多少度
②如果等腰三角形的底角等于40。,那么它的顶角的度数是多少 ③如果等腰三角形的顶角是400,那么它的底角的度数是多少 ④如果等腰三角形的一个角是40。,那么其他的两个角各是多少度
⑤如果等腰三角形的一个内角是l200,则其他的两个角各是多少度 ⑥等边三角形各内角有什么关系 各等于多少度
(3)在整个教学过程中,教师利用多种教学方法,使学生在实验中提出问题、解决问题,不知不觉地进入学习状态,使学生从被动学习变成主动想学。
教学启示:教师应始终坚持以学生为主体,致力启用学生已掌握的知识。充分调动学生的兴趣和积极性,使他们最大限度地参与到课堂的活动中,挖掘学生潜力,培养学生应用意识,提高学生的数学素养。
在“平行线的性质”的新授课上,一位教师设计了如下的教学片段:一、复习
1.如何用同位角、内错角、同旁内角来判定两条直线是否平行?
2.把它们已知和结论颠倒一下,可得到怎样的语句?"它们正确吗?二、新授
1.实验观察.发现平行线第一个性质。
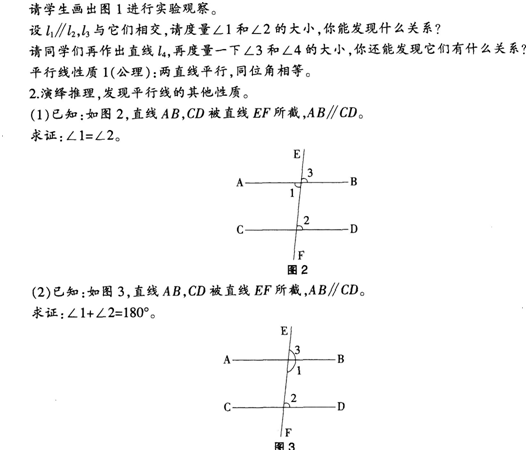
在此基础上指出:“平行线的性质2(定理)”和“平行线的性质3(定理)”。3.平行线判定与性质的区别与联系。
投影:将判定与性质各三条全部打出。
? ? (1)性质:根据两条直线平行,去证角的相等或互补。(2)判定:根据两角相等或互补,去证两条直线平行。联系是:它们的条件和结论是互逆的。性质与判定要证明的问题是不同的。
? ? 针对上述材料,完成下列任务。
? ? (1)本教学片段运用什么导入方法?并简述这种导入方法的优点。(7分)
? ?(2)简述本节课内容的教学目标。(5分)
? ? (3)本节课的重点和难点分别是什么?(5分)
? ? (4)为了进一步巩固平行线的性质定理,请设计相应例题和习题各一个,并写明解题思路。(13分)
- 参考答案:
- 您的答案:
参考解析:
(1)本教学片段运用了复习导人。这种导入方法利用新旧知识间的逻辑联系,即旧知识是新知识的基础,新知识是旧知识的发展与延伸,从而找出新旧知识联结的交点,由旧知识的复习迁移到新知识的学习上来导入新课。通过这种方法导入新课可以淡化学生对新知识的陌生感,使学生迅速将新知识纳入原有的知识结构中,能有效降低学生对新知识的认知难度。 (2)①理解平行线的性质和判定的区别:
②掌握平行线的三个性质,并能运用它们作简单的推理。(3)重点:平行线的三个性质。
难点:平行线的三个性质和怎样区分性质定理和判定定理。
(4)例题:如图所示,已知:AD//BC,∠AEF=∠B,求证:AD//EF。
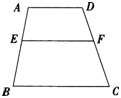
分析:(执果索因)从图直观分析,欲证AD//只需∠A+∠EF=1800
(由因求果)因为AD//BC,所以∠A+∠B=1800,又∠B=∠AEF,所以∠A+∠AEF=180。成立。于是得证。
证明:因为AD//BC.
所以∠A+∠B=1800。(两直线平行,同旁内角互补)因为£AE聘[曰,(已知)
所以∠A+∠AEF=1800,(等量代换)
所以AD//EF.(同旁内角互补,两条直线平行)
练习:如图所示,已知:AE平分∠BAC,C E ,且AB//CD。且AB∥CD
求证:∠l+∠2=900。
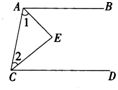
证明:因为AB//CD.
所以∠BAC+∠ACD=1800.
又因为AE平分∠BAC,CE平分∠ACD,