悬磁浮列车是一种科技含量很高的新型交通工具,它每个座位的平均能耗仅为飞机每个座位平均能耗的1/3,是汽车每个座位平均能耗的70%,那么汽车每个座位的平均能耗是飞机每个座位平均能耗的()
- A 21/10
- B 10/21
- C 3/7
- D 7/3
- 参考答案:B
- 您的答案:
参考解析:
这个的等量关系换算的媒介就是悬磁浮车,设置为单位1,飞机就是3,汽车10/7.再算汽车和飞机的差距。就是10/21
用10g糖、100g 水混合成糖水,糖和糖水的比是
- A 1:10
- B 10:1
- C 1:11
- 参考答案:C
- 您的答案:
参考解析:
把10克的糖放入100克的水中,糖水为(10+100)克,求糖和糖水的比,用糖的质量和糖水的质量相比
计算3a6÷a的结果是
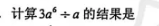
-
A
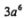
-
B
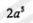
-
C
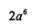
-
D
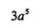
- 参考答案:D
- 您的答案:
参考解析:
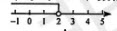
不等式x≤2在数轴上表示正确的是
-
A
-
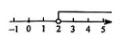
B
-
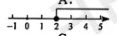
C
-
D
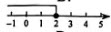
- 参考答案:D
- 您的答案:
参考解析:
如图,四边形ABCD内接于⊙O,若∠A=80°,则∠C的度数是
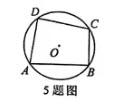
- A 80°
- B 100°
- C 110°
- D 120°
- 参考答案:B
- 您的答案:
参考解析:
缴纳个人所得税。张老师上月工资扣除所得税后是4761元,张老师上月缴纳个人所得税多少元?
- 参考答案:
(4761-3500)÷(1-3%)×3%=39(元)
答:张老师上月缴纳个人所得税39元
- 您的答案:
参考解析:
考点:存款利息与纳税相关问题.
此题属于纳税问题,关键是根据关系式:应缴税额部分×税率=缴纳的个人所得税,求出应缴的个人所得税即可.
根据题意,先求出超过3500元的部分,然后根据乘法的意义,解决问题.
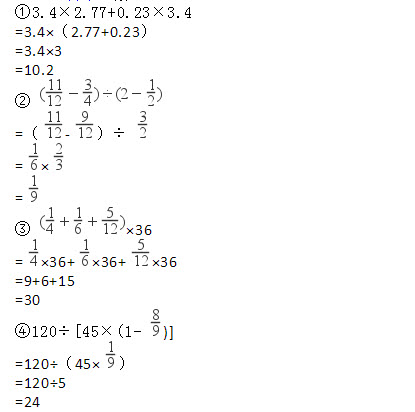
计算下面各题,能简算的要简算。
①3.4×2.77+0.23×3.4
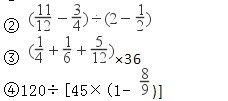
- 参考答案:
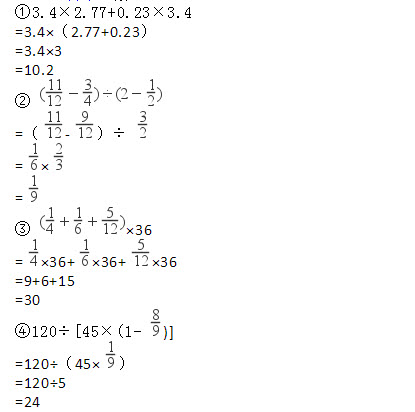
- 您的答案:
参考解析:
【考点】运算定律与简便运算,分数的四则混合运算,小数四则混合运算
【分析】本题考点:运算定律与简便运算;分数的四则混合运算;小数四则混合运算.
此题是考查四则混合运算,要仔细观察算式的特点,灵活运用一些定律进行简便计算.
(1)运用乘法结合律简算;
(2)通分后化简计算;
(3)运用乘法分配律简算;
(4)先算小括号里面的减法,再算中括号里面的乘法,最后算括号外的除法.
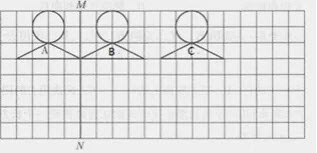
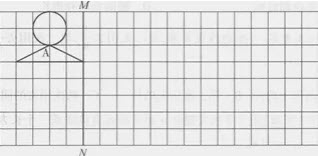
按要求绘制图形。
(i)以直线MN为对称轴做图形A的轴对称图形,得到图形B。
(ii)将图形B向右平移5格,的到图形C。
- 参考答案:

- 您的答案:
参考解析:
本题考点:作轴对称图形;作平移后的图形.
本题是考查作轴对称图形,关键是对称点的选取.
根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在MN的右边画出左边图形的外面多边形的五个顶点,然后连结,再画出上面的圆,以1格为半径画圆,再选择多个顶点平行往右移动5格,作出图c.
王大妈在三块菜地里种了1200棵番茄,第一块菜地里种的番茄棵数是第二块菜地的3/4,第三块菜地里种的番茄棵数是第二块菜地的5/4。三块菜地里各种番茄多少棵?
- 参考答案:
1200÷(1+3/4+5/4)=400(棵)
400X3/4=300(棵)
400X5/4=500(棵)
答:第一块菜地里种番茄300棵,第二块菜地里种番茄400棵,第三块菜地里种番茄500棵
- 您的答案:
参考解析:

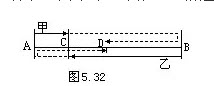
甲、乙两车从开始到第一次C点相遇时,合起来行了一个全程。此时甲行了30千米,从第一次相遇到第二次D点相遇时,两车合起来行了两个全程。在这两个全程中,乙共行(30+42)千米,所以在合行一个全程中,乙行(30+42)÷2=36(千米),即A、B两城的距离是30+36=66(千米)。
" data-timutype="tian" data-ci="0" data-orderid="10">甲、乙两车分别从A、B两城同时相向而行,第一次在离A城30千米处相遇。相遇后两车又继续前行,分别到达对方城市后,又立即返回,在离A城42千米处第二次相遇。求A、B两城的距离。
- 参考答案:
讲析:如图5.32所示。两车第一次在C地相遇,第二次在D地相遇。
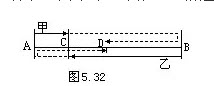
甲、乙两车从开始到第一次C点相遇时,合起来行了一个全程。此时甲行了30千米,从第一次相遇到第二次D点相遇时,两车合起来行了两个全程。在这两个全程中,乙共行(30+42)千米,所以在合行一个全程中,乙行(30+42)÷2=36(千米),即A、B两城的距离是30+36=66(千米)。
- 您的答案:
