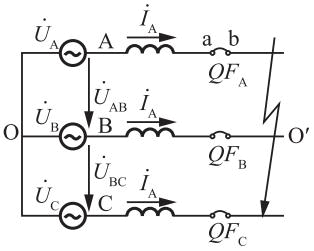
设y=0平面是两种介质的分界面,在y>0区域内,ε1=5ε0;在y<0区域内,ε2=3ε0,在此分界面上无自由电荷。已知E1=(10ex+12ey)V/m,则E2为( )。
- A (10ex+20ey)V/m
- B (20ex+10ey)V/m
- C (10ex-20ey)V/m
- D (20ex-100ey)V/m
- 参考答案:A
- 您的答案:
参考解析:
两个介质分界面的基本方程为:E1t=E2t,D1n-D2n=σ,即分界面两侧相邻点的电场强度切向分量相等,电位法向分量之差为分界面的自由电荷面密度σ。当分界面无自由电荷时,D1n=D2n。因为tanφ1=10/12=5/6,又由分界条件可得:tanφ2/tanφ1=ε2/ε1=35,tanφ2=0.5,E2t=E1t=10ex,E2n=10/0.5=20ey,则E2=10ex+20eyV/m。
在棒-板电极形成的极不均匀电场中,在棒电极的极性不同的情况下,起始电晕电压和放电电压的特性为( )。
- A 负极性、高、高
- B 正极性、高、低
- C 负极性、高、低
- D 正极性、高、高
- 参考答案:B
- 您的答案:
参考解析:
棒-板间隙是典型的极不均匀电场,这种间隙中,电离过程总是先从棒电极附近开始,棒的极性不同时,空间电荷的作用是不同的,存在极性效应。电晕放电阶段:当棒电极为正极性时,滞留在棒极附近的正空间电荷加强了朝向板极方向的电场,而减弱了朝向棒极的电场。因此,朝向板极方向的电子崩容易形成,有利于放电向前发展,即击穿电压较低。而棒极附近由于电场较弱,发生电晕比较困难,即起晕电压较高。
一幅值为U=1200kV的直角雷电波击中波阻抗为250Ω、150km长的无损空载输电线路的首端,波传播到线路末端时,末端电压为( )。
- A 1200kV
- B 2400kV
- C 1600kV
- D 1800kV
- 参考答案:B
- 您的答案:
参考解析:
由于线路为空载状态,即线路末端开路,相当于Z2=∞,说明入射波U0到达开路的末端后将发生全反射。全反射的结果是使线路末端电压上升到入射波电压的两倍。随着反射电压波的反行,导线上的电压降逐渐上升至入射波的两倍,未达到反射之处仍为U0;在电压发生全反射的同时,电流则发生了负的全反射,电流负反射的结果使线路末端的电流为零,而随着反射电流波的反行,导线上的电流将逐渐下降为零。
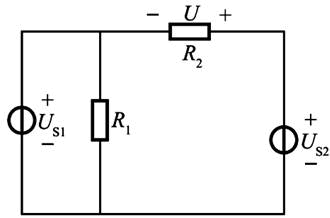
图示电路中,已知R1=10Ω,R2=2Ω,US1=10V,US2=6V。电阻R2两端的电压U为( )。
- A 4V
- B 2V
- C -4V
- D -2V
- 参考答案:C
- 您的答案:
参考解析:
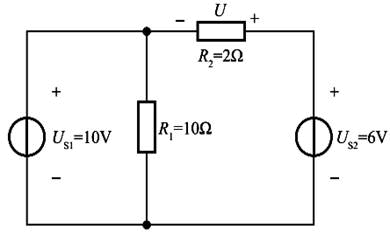
如题解图所示,根据基尔霍夫电压定律可得:US1+U=US2,代入数据,则UR2=U=US2-US1=6-10=-4V。因其与题解图中R2所标电压方向相反,故取负值。
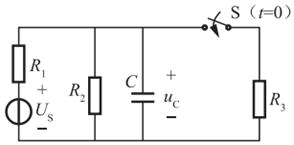
图示电路中,已知US=6V,R1=1Ω,R2=2Ω,R3=4Ω,开关闭合前电路处于稳态,t=0时开关S闭合。t=0+时,uC(0+)为( )。
- A -6V
- B 6V
- C -4V
- D 4V
- 参考答案:D
- 您的答案:
参考解析:
t=0-时,等效电路如题解图所示。由电阻分压定理易知:uC(0-)=R2US/(R1+R2)=2×6/(1+2)=4V。开关S闭合前,原稳定电路中电容电压已达到稳定,电容为储能元件。由换路定则知,开关S闭合前后,电容电压不会发生突变,则:uC(0+)=uC(0-)=(6/3)×2=4V。
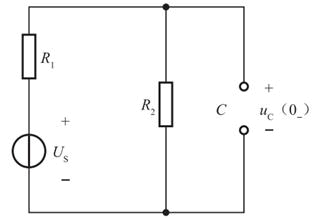
一台SN=5600kVA,U1N/U2N=6000/4000V,Y/Δ联接的三相变压器,其空载损耗P0=18kW,短路损耗PkN=56kW,当负载的功率因数cosφ2=0.8(滞后),保持不变,变压器的效率达到最大值时,变压器一次边输入电流为( )。
- A 305.53A
- B 529.2A
- C 538.86A
- D 933.33A
- 参考答案:A
- 您的答案:
参考解析:
在负载性质不变的情况下(cosφ2=常数),当铁耗与铜耗相等时,变压器效率达到最大,此时负载系数为:
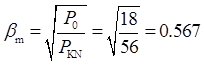
负载系数为二次电流和二次额定电流的比值,即β=I2/I2N=I1/I1N。又因为:
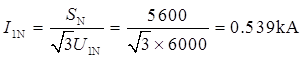
则变压器一次侧输入电流为:I1=βmI1N=0.567×0.539=305.53A。
一台三相感应电动机PN=1000kW,电源频率f为50Hz,额定电压UN=6kV,接法,功率因数cosφ=0.75,效率ηN=0.92,绕组系数Kw1=0.945,定子绕组每相串联匝数N1=92,已知电机的励磁电流Im=45%In,求其三相基波旋转磁势幅值为( )。
- A 4803.3安匝
- B 9607.6安匝
- C 21346.7安匝
- D 16367.8安匝
- 参考答案:D
- 您的答案:
参考解析:
三相感应电动机的额定相电流为:
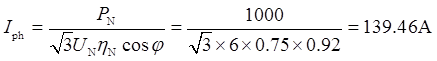
三相基波磁动势幅值为:F1=1.35N1IphKw1=1.35×92×139.46×0.945=16368.3安匝。
绕线式异步电动机拖动恒转矩负载运行,当转子回路串入不同电阻,电动机转速不同,而串入电阻与未串入电阻相比,对转子的电流和功率因数的影响是( )。
- A 转子电流大小和功率因数均不变
- B 转子电流大小变化、功率因数不变
- C 转子电流大小不变、功率因数变化
- D 转子电流大小和功率因数均变化
- 参考答案:A
- 您的答案:
参考解析:
恒转矩负载运行时,由T=CTΦmI2′cosφ2可知,在电源电压一定时,主磁通Φm也一定。在转子串入电阻后仍保持转子电流不变,因此功率因数cosφ2也保持不变,设原来转子电阻为R2,电流为I2N,转差率为SN,则转子电流为:
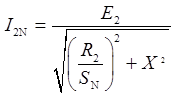
转子串入电阻RS后,转差率变为S,则电流变化为:
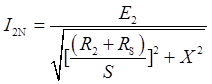
因此,(R2+RS)/S=R2/SN,可见转子串入电阻时,其转差率将相应变化。
由三台相同的单相变压器组成的YNy0联接的三相变压器,相电势的波形是( )。
- A 正弦波
- B 方波
- C 平顶波
- D 尖顶波
- 参考答案:D
- 您的答案:
参考解析:
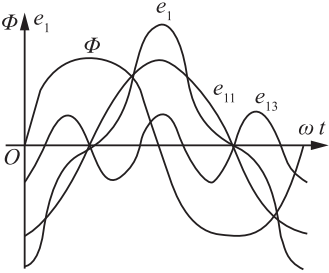
三台相同的单相变压器即为三相组式变压器,分析如下:三相组式变压器磁路相互独立,彼此不相关联。当励磁电流为正弦波,由于磁路的非线性,主磁通为平顶波,主磁通Φ中三次谐波磁通Φ3和基波磁通Φ1一样,可以沿铁芯闭合。在铁芯饱和的情况下,三次谐波含量较大,可达到基波磁通的15%~20%。又因为三次谐波磁通在绕组中感应出三次谐波电动势e13,其频率是基波的3倍,故三次谐波电动势e13的幅值可达基波电动势e11幅值的45%~60%,甚至更大,将e13和e11相加,即得到尖顶波形的相电动势(见题解图)。
题解图平顶波磁通产生的电动势波形
电力系统接线如图所示,各级电网的额定电压示于图中,发电机、变压器T1、T2的额定电压分别为( )。
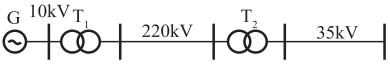
- A G:10.5kV,T1:10.5/242kV,T2:220/38.5kV
- B G:10kV,T1:10/242kV,T2:242/35kV
- C G:10.5kV,T1:10.5/220kV,T2:220/38.5kV
- D G:10.5kV,T1:10.5/242kV,T2:220/35kV
- 参考答案:A
- 您的答案:
参考解析:
电网及设备电压的基本原则如下:
①发电机额定电压规定比网络额定电压高5%,即VGN=(1+5%)×10=10.5kV。
②变压器一次绕组相当于用电设备,其额定电压等于网络额定电压,但与发电机直接连接时,等于发电机额定电压。
③变压器二次绕组相当于供电设备,故一般额定电压比网络高5%~10%(UK%<7%,取5%;UK%>7%,取10%),即:VT1=10.5/220×(1+10%)=10.5/242kV,VT2=220/35×(1+10%)=220/38.5kV。
长距离输电线路,末端加装电抗器的目的是( )。
- A 吸收容性无功功率,升高末端电压
- B 吸收感性无功功率,降低末端电压
- C 吸收容性无功功率,降低末端电压
- D 吸收感性无功功率,升高末端电压
- 参考答案:C
- 您的答案:
参考解析:
线路空载时,线路末端的功率为零,根据П形输电线路等值电路,得到公式:
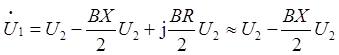
由上述公式可知,高压输电线路空载或轻载时,都会产生末端电压升高的现象,常用的措施是在线路末端加装并联电抗器,用它来吸收线路分布电容所产生的容性电流,避免线路末端电压超过允许值,导致设备绝缘损坏。
为使断路器弧熄电压恢复过程为非周期性的,可在断路器触头两端( )。
- A 并联电容
- B 并联电抗
- C 并联电阻
- D 辅助触头
- 参考答案:C
- 您的答案:
参考解析:
交流电弧每半周期自然熄灭是熄灭交流电弧的最佳时机。实际上在电流过零后弧隙中存在两个恢复过程:介质强度恢复过程Ud(t)和弧隙电压恢复过程Ur(t)。交流电弧熄灭的条件为:Ud(t)>Ur(t)。如果能够采取措施防止Ur(t)振荡,将周期性振荡特性的恢复电压转变为非周期性恢复过程,电弧就更容易熄灭。
常用的做法是在断路器触头两端并联电阻。当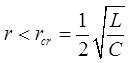 时,可将弧隙恢复电压由周期性振荡特性恢复电压转变为非周期性,从而大大降低了恢复电压的上升速度和幅值,改善了断路器的灭弧条件。
时,可将弧隙恢复电压由周期性振荡特性恢复电压转变为非周期性,从而大大降低了恢复电压的上升速度和幅值,改善了断路器的灭弧条件。
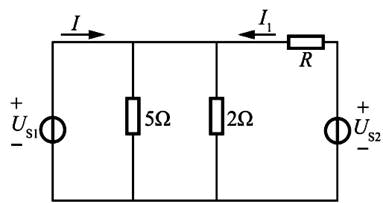
图示电路中,测得US1=10V,电流I=10A。流过电阻R的电流I1为( )。
- A 3A
- B -3A
- C 6A
- D -6A
- 参考答案:B
- 您的答案:
参考解析:
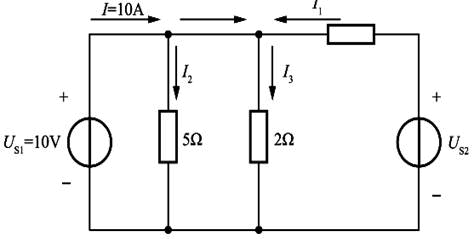
如题解图所示,根据欧姆定律得:I2=Us1/5=10/5=2A,I3=Us1/2=10/2=5A,根据基尔霍夫电流定律可得:10-I2+I1=I3。因此,I1=-3A。
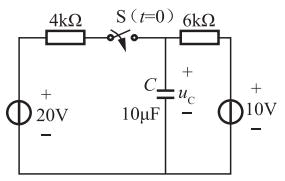
图示电路中,开关S闭合前电路已处于稳态,在t=0时开关S闭合,开关闭合后的uC(t)为( )。
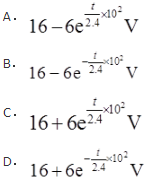
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
采用三要素法求解响应方程,步骤如下:
①求换路前后电容电压的初始值和稳态值,开关闭合前,电容电压的初始值:uC(0-)=10V,根据换路定则可知,开关S闭合前后电容电压不突变,则uC(0+)=uC(0-)=10V,开关闭合后电路如题15解图(a)所示,则电容电压的稳态值为:uC(∞)=(20-10)/(4+6)×6V+10V=16V。
②求解时间常数τ,根据题15解图(b)求得等效电阻为:R=R1×R2/(R1+R2)=4×6/(4+6)×10^3Ω=2.4×10^3Ω,则时间常数τ=RC=2.4×103Ω×10×10-6F=2.4×10-2s。
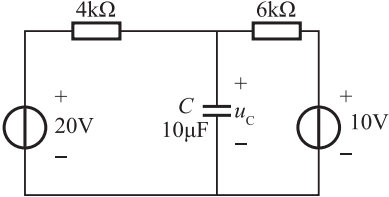
③根据三要素公式可得uC(t)为:
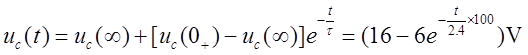
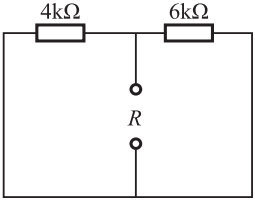
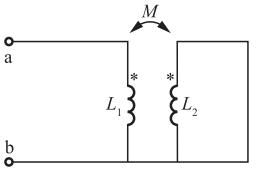
图示含耦合电感电路中,已知L1=0.1H,L2=0.4H,M=0.12H,ab端的等效电感Lab为( )。
- A 0.064H
- B 0.062H
- C 0.64H
- D 0.62H
- 参考答案:A
- 您的答案:
参考解析:
去耦等效电路如题17解图所示。将数据代入,则等效电感为:Leq=(L1-M)+[(L2-M)∥M]=(0.1-0.12)+[(0.4-0.12)∥0.12]=0.064H。

要获得32k×8的RAM,需要4k×4的RAM的片数为( )。
- A 8个
- B 16个
- C 32个
- D 64个
- 参考答案:B
- 您的答案:
参考解析:
32k×8的RAM表示8位的随机读写存储器,每片的可存储的容量为32×1024×8B,4k×4的可存储数据容量为4×1024×4B。因此扩展时保证数据存储的总容量大小不变,求得需用4k×4的RAM的片数为:n=32×1024×8/(4×1024×4)=16(片)。
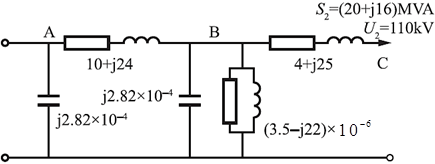
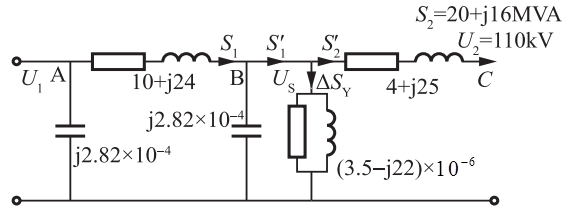
有一线路和变压器组成的简单电力系统归算到高压侧的等值电路如图所示,线路及变压器的参数标在图中,当C点实际电压为110∠0°kV,线路末端并联支路功率及输入变压器的功率分别为:(不考虑电压降落横分量)( )。
- A -j2.688MVA,20.22+j17.65
- B -j3.688MVA,23.15+j19.32
- C -j2.688MVA,23.15+j19.32
- D -j3.688MVA,20.22+j17.65
- 参考答案:D
- 您的答案:
参考解析:
等效电路如题46解图所示,各功率及电压标注图中。
变压器串联支路电压降落纵分量为:U=(P2R+Q2X)/U2=(204+1625)/110=4.364kV。
忽略电压降落横分量,则UB=U2+ΔU=110+4.364=114.364k。
线路末端并联支路功率为:

我国电力系统中性点直接接地方式一般在下列哪个电压等级的电网中使用( )
- A 10kV及以上
- B 35kV及以上
- C 110kV及以上
- D 220kV及以上
- 参考答案:C
- 您的答案:
参考解析:
我国110kV及以上电网一般采用中性点直接接地方式。6~35kV配电网一般采用小电流接地方式,即中性点非有效接地方式,包括中性点不接地、高阻接地、经消弧线圈接地方式等。为了使电弧容易熄灭,在电容电流较大的35kV和10kV电网中采用中性点经消弧线圈接地。
3~20kV电网中,为了测量对地电压,通常采用下列哪种电压互感器( )
- A 三相三柱式
- B 三相五柱式
- C 三台单相式
- D 两台单相式
- 参考答案:B
- 您的答案:
参考解析:
各电压互感器的接线及使用范围表述如下:
①两台单相电压互感器接成不完全星形或V—V接线,因其原副边均无中性点可接地,因此无法测量相对地电压。
②三相三柱式电压互感器,不允许将电压互感器高压侧中性点接地,因此无法测量相对地电压。
③三相五柱式电压互感器,高低压侧中性点均接地,可以测量相对地电压,另外开口三角形还可测量零序电压。
④副边接成三角形,肯定不能测量相对地电压。
提高悬式绝缘子耐污性能的方法是下列哪一项( )
- A 改善绝缘子电位分布
- B 涂憎水性涂料
- C 增加绝缘子爬距
- D 增加绝缘子片数
- 参考答案:B
- 您的答案:
参考解析:
绝缘子的雷电闪络电压最大的影响因素是电弧距离,一般可采取如下措施:
①提高憎水性。可使绝缘子表面的水分以小水珠的形式出现,难以形成连续的水膜,在持续电压的作用下,表面不易形成集中放电的通道,从而有效提高污闪电压。
②增加爬电距离。爬电距离是指沿绝缘表面测得的两个导电器件或导电器件与设备界面之间的最短距离,主要用来确定绝缘子,如支持绝缘子的长度和绝缘子串的数量。
③改善电位分布:绝缘子电场强度不均匀是绝缘子污闪电压低的重要原因。改善电位分布,抑制带电粒子迁移,降低泄漏电流,可大幅度提高单个绝缘子的污闪电压(如均压环),实际也可提高绝缘子串的闪络电压,但这不是该措施的主要效果。
本题中,ABCD四项都是工程中可采用的提高绝缘子耐污性能的方法。其中,ACD三项一般用在绝缘子选型时;而B项可以应用在提高现有绝缘子耐污性能上,应用也更广泛。
雷电冲击电压波在线路中传播时,为何会出现折射现象( )
- A 线路阻抗大
- B 线路阻抗小
- C 线路有节点
- D 线路有雷电感应电压波
- 参考答案:C
- 您的答案:
参考解析:
当所研究的线路长度与电磁波波长可比时,此时应该采用分布参数电路的特定求解方法。工程中常会遇到一条长线与另一条波阻抗不同的长线相连或一条长线与几种参数的元件相连的情况。当行波达到不同波阻抗的连接点,此时电压、电流、能量需要进行重新调整、分配,所以在节点处会发生波的反射与折射。
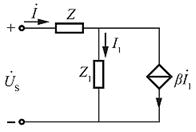
图示正弦交流电路中,已知Z=10+j50Ω,Z1=400+j1000Ω,当β为下列哪项数值时,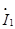 和
和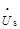 的相位差为90°( )
的相位差为90°( )
- A -41
- B 41
- C -51
- D 51
- 参考答案:A
- 您的答案:
参考解析:

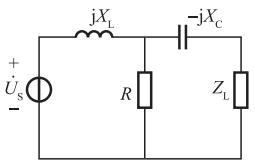
图示正弦交流电路中,已知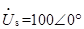 V,R=10Ω,XL=20Ω,XC=30Ω,当负载ZL为下列哪项数值时,它将获得最大功率( )
V,R=10Ω,XL=20Ω,XC=30Ω,当负载ZL为下列哪项数值时,它将获得最大功率( )
- A 8+j21Ω
- B 8-j21Ω
- C 8+j26Ω
- D 8-j26Ω
- 参考答案:C
- 您的答案:
参考解析:
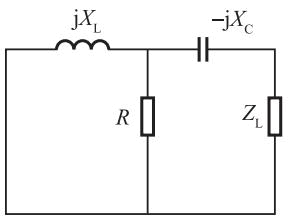
最大功率传输条件是:去掉负载阻抗后,计算戴维南等效电路中的内阻抗Zin,当负载阻抗和内阻抗Zin的共轭相等时,即ZL=Z*in,在负载中可获得最大功率。将图中独立电源置零(电压源短路),其电路如题解图所示,可得等效电路的内阻抗为:Zin=(j20∥10)+(-j30)=8-j26Ω。根据最大功率传输条件,最佳匹配为:ZL=8+j26时获得最大功率。
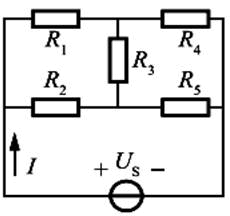
图示电路中,已知US=12V,R1=15Ω,R2=30Ω,R3=20Ω,R4=8Ω,R5=12Ω,电流I为( )。
- A 2A
- B 1.5A
- C 0.8A
- D 0.5A
- 参考答案:C
- 您的答案:
参考解析:
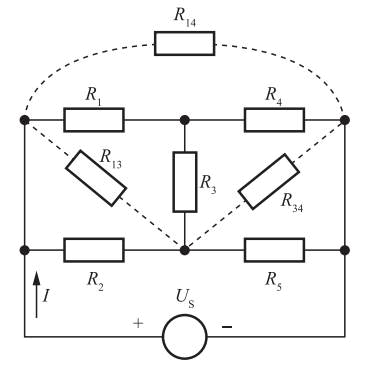
如题解图所示。对题图电路作星-三角等效变换得:R13=R3+R1+R3×R1/R4=72.5Ω,R34=R4+R3+R4×R3/R1=38.7Ω,R14=R4+R1+R4×R1/R3=29Ω。因此,等效电阻X∑=29∥[72.5∥30+38.7∥12]=14.83Ω,电流为:I=U/R∑=12/14.83=0.81A。
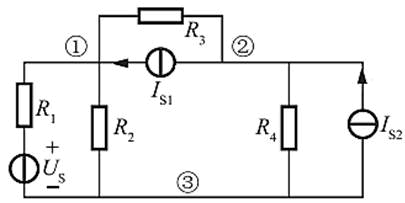
图示电路中,已知US=12V,IS1=2A,IS2=8A,R1=12Ω,R2=6Ω,R3=8Ω,R4=4Ω。取结点③为参考结点,结点①的电压Un1为( )。
- A 15V
- B 21V
- C 27V
- D 33V
- 参考答案:A
- 您的答案:
参考解析:
设节点3电压为0,即将节点3接地,列节点电压方程为:
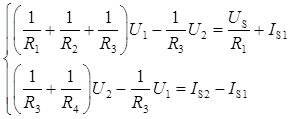
代入数值可得:
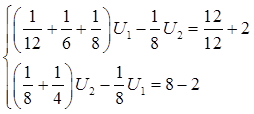
解方程可得:U1=15V,U2=21V。
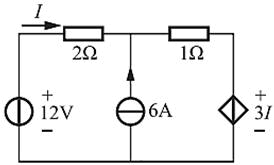
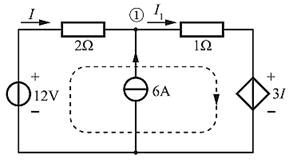
图示电路中,电流I为( )。
- A -2A
- B 2A
- C -1A
- D 1A
- 参考答案:D
- 您的答案:
参考解析:
如题解图所示,对节点①,根据基尔霍夫电流定律得:I1=I+6A。根据图中所示回路,根据基尔霍夫电压定律得:12-3I=2I+(I+6)×1,解得I=1A。
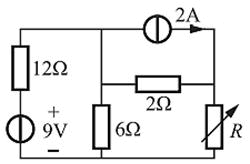
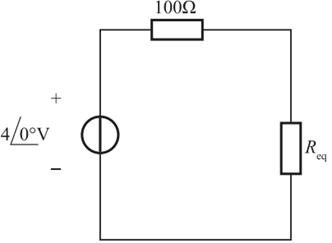
图示电路中的电阻R阻值可变,R为下列哪项数值时可获得最大功率( )
- A 12Ω
- B 15Ω
- C 10Ω
- D 6Ω
- 参考答案:D
- 您的答案:
参考解析:
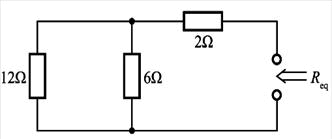
最大功率传输条件是:当负载电阻等于去掉负载后的戴维南等效电路的内阻Rin时,在负载中可获得最大功率。将图中两个独立电源置零(电流源开路,电压源短路),可得二端网络等效内阻电路如题解图所示,则Rin=(12∥6)+2=6Ω,所以当R=6Ω时,可获得最大功率。其最大功率为PM=Us2/4Req,式中Us为戴维南等效电路的电源电压。
图示电路中的R、L串联电路为日光灯的电路模型。将此电路接于50Hz的正弦交流电压源上,测得端电压为220V,电流为0.4A,功率为40W。电路吸收的无功功率Q为( )。

- A 76.5Var
- B 78.4Var
- C 82.4Var
- D 85.4Var
- 参考答案:B
- 您的答案:
参考解析:
测量功率为电阻R消耗的有功功率,故P=UIcosθ=220×0.4×cosθ=40W,则cosθ=5/11,所以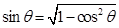 ,因此,电路吸收的无功功率为:
,因此,电路吸收的无功功率为:
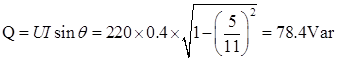
在题7中,如果要求将功率因数提高到0.95,应给日光灯并联的电容C为( )。
- A 4.29μF
- B 3.29μF
- C 5.29μF
- D 1.29μF
- 参考答案:A
- 您的答案:
参考解析:
并联C后,电路有功功率40W不变,功率因数提高到0.95,即cosφ=0.95,则tanφ=0.33,无功功率为:Q=Ptanφ=40×0.33=13.2Var。由于无功守恒,则Q=QL+QC=78.4+QC,因此,电容的无功功率为:QC=-65.2Var。由于Q=-U2/XC,代入数据解得:XC=742.33Ω。又可知XC=1/(ωC),则C=1/(2πfXC)=1/(2π×50×742.33)=4.29μF。
在RC串联电路中,已知外加电压:u(t)=20+90sin(ωt)+30sin(3ωt+50°)+10sin(5ωt+10°)V,电路中电流:i(t)=1.5+1.3sin(ωt+85.3°)+6sin(3ωt+45°)+2.5sin(5ωt-60.8°)A,则电路的平均功率P为( )。
- A 124.12W
- B 128.56W
- C 145.28W
- D 134.28W
- 参考答案:B
- 您的答案:
参考解析:
平均功率是直流分量的功率与各次谐波平均功率的代数和,即:P=P0+P1+P3+P5=U0I0+U1I1cosφ1+U3I3cosφ3+U5I5cosφ5=30+117/2×cos(-85.3°)+(180/2)×cos5°+25/2×cos70.8°=30+4.79+89.66+4.11=128.56W。
图示RLC串联电路中,已知R=10Ω,L=0.05H,C=50μF,电源电压为:u(t)=20+90sin(ωt)+30sin(3ωt+45°)V,电源的基波角频率ω=314rad/s,电路中的电流i(t)为( )。
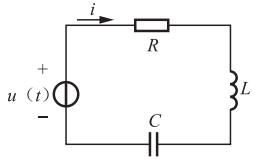

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
如题解图所示。运用叠加定理进行计算,先将各分量计算出来再进行叠加。直流电流对于RC串联电路相当于断路,因此无直流电流分量。
基频时:X1L=ωL=314×0.05=15.7Ω;X1C=1/ωC=1/314×50×10-6=63.7Ω;总阻抗为:Z1=10+j(15.7-63.7)=10-j48=49∠-78.2°Ω。
三次频率时:X3L=3ωL=3×314×0.05=47.1Ω;X3C=1/3ωC=1/3×314×50×10-6=21.2Ω;总阻抗为:Z3=10+j(47.1-21.2)=10+j25.9=27.76∠68.9°Ω。
则电流方程为:i(t)=u(t)/Z=90/49×sin[ωt-(-78.2°)]+30/27.76×sin[3ωt+(45-68.9°)]=1.837sin(ωt+78.2°)+1.08sin(3ωt-23.9°)。
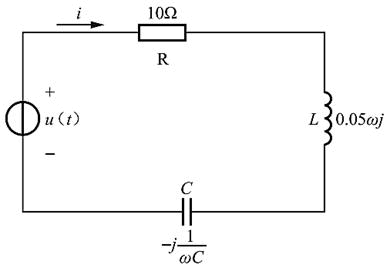
图示电路中,已知R1=3Ω,R2=R3=2Ω,US=10V,开关S闭合前电路处于稳态,t=0时开关闭合,t=0+时,iL1(0+)为( )。
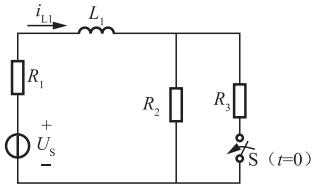
- A 2A
- B -2A
- C 2.5A
- D -2.5A
- 参考答案:A
- 您的答案:
参考解析:
t=0-时,等效电路如题解图所示。开关S闭合前电路处于稳态,电感相当于短路,则:iL1(0-)=1/(R1+R2)×US=10/(3+2)=2A,由换路定律知,开关S闭合前后,电感电流不能突变,因此,iL1(0+)=iL1(0-)=2A。
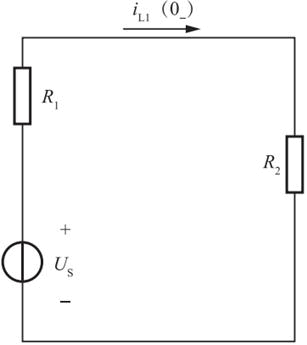
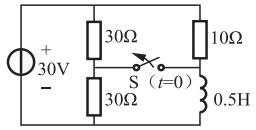
图示电路中,换路前已处于稳定状态,在t=0时开关S打开,开关S打开后的电流i(t)为( )。
- A 3-e^20tA
- B 3-e^-20tA
- C 3+e^-20tA
- D 3+e^20tA
- 参考答案:C
- 您的答案:
参考解析:
用三要素法求电感电流的响应方程,步骤如下:
①求出电感电流在换路前后的初始值,根据换路定则有:iL1(0+)=iL1(0-)=30V/(30Ω∥10Ω)=4A。
②求解换路后电感电流的稳态值,如题16解图所示,开关S打开后,电路达到新的稳态,电感视作短路,则电感的稳态值为:iL(∞)=30V/10Ω=3A。
③求时间常数τ,将电压源短路,电感的等效串联电阻R=10Ω。则时间常数为:τ=L/R=0.5H/10Ω=0.05s。
根据三要素公式可得:iL(t)=iL(∞)+[iL(0+)-iL(∞)]e-t/τ=(3+e-20t)A。
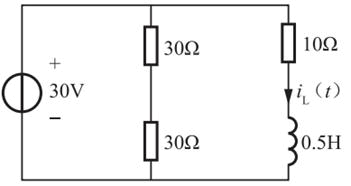
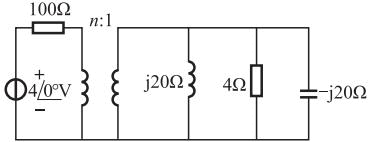
图示电路中,n为下列哪项数值时,R=4Ω电阻可以获得最大功率( )
- A 2
- B 7
- C 3
- D 5
- 参考答案:D
- 您的答案:
参考解析:
电感和电容阻抗大小相等,若所在的支路发生并联谐振,相当于断路,阻抗无穷大。由最大功率传输定理知,当负载电阻等于等效电路的内阻时,负载将获得最大功率。电路图如题18解图所示,Req为二次侧的等效电路的内电阻,根据最大功率传输条件可知当Req=100时获得最大功率,即:n2×4=100,所以n=5。
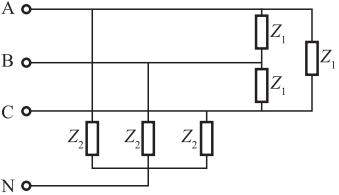
图示对称三相电路中,已知线电压U1=380V,负载阻抗Z1=-j12Ω,Z2=3+j4Ω,三相负载吸收的全部平均功率P为( )。
- A 17.424kW
- B 13.068kW
- C 5.808kW
- D 7.42kW
- 参考答案:A
- 您的答案:
参考解析:
由题图知,负载Z1为纯电容负载,不吸收有功功率,负载Z2吸收有功功率。设相电压为: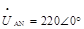 ,先进行星-三角转换,则Z1′=Z1/3=-j12/3=-j4Ω。总等效阻抗为:Zeq=Z1′∥Z2=-j4∥(3+j4)=-j4(3+j4)/(3+j4-j4)=20/3∠-36.87°。相电流IAN=UAN/Zeq=3×220∠0°/20∠-36.87°=33∠36.87°,则电路平均功率为:P=3UANIANcosφ=3×220×33×cos36.87°=17424W=17.424kW。
,先进行星-三角转换,则Z1′=Z1/3=-j12/3=-j4Ω。总等效阻抗为:Zeq=Z1′∥Z2=-j4∥(3+j4)=-j4(3+j4)/(3+j4-j4)=20/3∠-36.87°。相电流IAN=UAN/Zeq=3×220∠0°/20∠-36.87°=33∠36.87°,则电路平均功率为:P=3UANIANcosφ=3×220×33×cos36.87°=17424W=17.424kW。
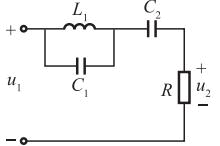
图示电路中,已知L1=0.12H,ω=314rad/s,u1(t)=U1mcos(ωt)+U3mcos(3ωt),u2(t)=U1mcos(ωt),C2和C2的数值分别为下列哪种数值( )
- A 7.39μF和71.14μF
- B 71.14μF和7.39μF
- C 9.39μF和75.14μF
- D 75.14μF和9.39μF
- 参考答案:C
- 您的答案:
参考解析:
根据输出电压只含有基频分量,可知基频时,发生串联谐振;三次谐频时,发生并联谐振,则:
①三次频率时(电路发生并联谐振,电容电感并联回路相当于断路):1/(3ωC1)=3ωL1,因此,C1=1/(9ω2L1)=1/(9×3142×0.12)=9.39×10-6F=9.39μF。
②基频时(电路发生串联谐振,回路相当于短路):容抗XC1=(ωC1)-1=314×9.39×10-6=339Ω,感抗XL1=ωL1=314×0.12=37.68Ω,则XL1∥XC1=j37.68∥(-j339)=j42.39Ω。又因为XC2+XL1∥XC1=0,所以电容C2=1/(314×42.39)=75.13×10-6F=75.13μF。
图示电路中,换路前已达稳态,在t=0时开关S打开,欲使电路产生临界阻尼响应,R应取下列哪项数值(精确到小数点后二位)( )。
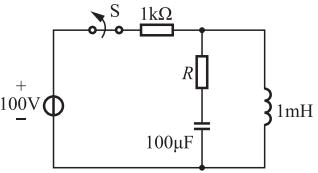
- A 3.16Ω
- B 6.33Ω
- C 12.66Ω
- D 20Ω
- 参考答案:B
- 您的答案:
参考解析:
由题21图可知,开关S打开后,形成了二阶RLC串联电路,且无独立电压,为零输入响应。其微分方程为:
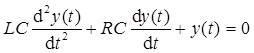
特征方程为:LCs2+RCs+1=0,则Δ=(RC)2-4LC=C2(R2-4L/C)。
二阶电路的特征根由于电路中R、L、C的参数不同可能有以下三种情况:
①当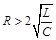 时,特征根为两个不等实根,为过阻尼非振荡过程;
时,特征根为两个不等实根,为过阻尼非振荡过程;
②当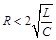 时,特征值是一对共轭复根,为欠阻尼振荡放电过程;
时,特征值是一对共轭复根,为欠阻尼振荡放电过程;
③当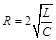 时,为临界振荡,各变量随时间的变化和非振荡过程相仿。
时,为临界振荡,各变量随时间的变化和非振荡过程相仿。
本题中,当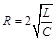 时,电路产生临界阻尼,则=6.33Ω。
时,电路产生临界阻尼,则=6.33Ω。
在RCL串联谐振电路中,R=10Ω,L=20mH,C=200pF,电源电压U=10V,电路的品质因数Q为( )。
- A 3
- B 10
- C 100
- D 1000
- 参考答案:D
- 您的答案:
参考解析:
品质因数Q表征一个储能器件(如电感线圈、电容等)、谐振电路的储能量同每周期损耗能量之比的一种质量指标。元件的Q值越大,用该元件组成的电路或网络的选择性越佳。对于不同电路的品质因数计算方法如下:
无辐射系统:Q=无功功率/有功功率=|X|/R;
串联谐振:Q=特性阻抗/回路电阻=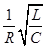 ;
;
特性阻抗: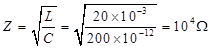 。
。
因此,品质因数Q=10^4/R=1000。
真空中有一线密度τ沿Z轴均匀分布的无限长线电荷,P点距离Z轴垂直距离为ρ,则距离导线τ处一点P的电场强度E为( )。
- A τ/(4πε0ρ)V/m
- B τ/(2πε0ρ)V/m
- C τ/(4πε0ρ2)V/m
- D τ/(2πε0ρ2)V/m
- 参考答案:B
- 您的答案:
参考解析:

真空中相距为a的两无限大平板,电荷面密度分别为+δ和-δ,这两个带电面之间的电压U为( )。
- A δa/(2ε0)V
- B δa/ε0V
- C δa/(3ε0)V
- D δa/(4ε0)V
- 参考答案:B
- 您的答案:
参考解析:
真空中无限大带电平面的电场强度为:E(x)=δ/(2ε0)。因此,两平面之间的电场强度E(x)=δ/(2ε0)+δ/(2ε0)=δ/ε0(场强的方向由+δ指向-δ),则两个带电面之间的电压为:
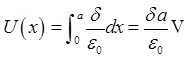
在恒定电场中,若两种不同的媒质分界面为xoz平面,其上有电流线密度K=2exA/m,已知H1=(ex+2ey+3ez)A/m,μ1=μ0,μ2=2μ0,则H2为( )。
- A (3ex+2ey+ez)A/m
- B (3ex+ey+3ez)A/m
- C (3ex+ey+ez)A/m
- D (ex+ey+3ez)A/m
- 参考答案:B
- 您的答案:
参考解析:
根据磁场分界面条件,两个介质分界面的基本方程为:H1t-H2t=JS和B1n=B2n。H1的x方向和z方向分量构成分界面处的切向分量,可列方程:H1z-H2z=0,H1x-H2x=-2。经计算解方程得:H2z=H1z=3,H2x=H1x+2=3。H1中的y方向分量构成分界面处的法向分量,可得:B1n=B2n,所以μ1H1y=μ2H2y,则H2y=μ1H1y/μ2=1。因此,H2=(3ex+ey+3ez)A/m。
一条长度为λ/4的无损耗传输线,特性阻抗为Z0,终端接负载ZL=RL+jXL,其输入阻抗相当于一电阻Ri与电容Xi并联,其数值为( )。
- A RLZ0和XLZ0
- B Z20/XL和Z20/RL
- C Z20/RL和Z20/XL
- D RLZ20和XLZ20
- 参考答案:C
- 您的答案:
参考解析:

图示电路中,A为理想运算放大器,三端集成稳压器的2、3端之间的电压用UREF表示,则电路的输出电压可表示为( )。
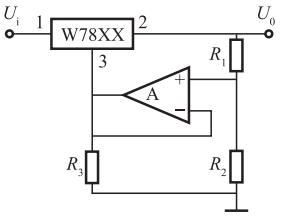
- A U0=(U1+UREF)R2/R1
- B U0=U1+R2/R1
- C U0=UREF(1+R2/R1)
- D U0=UREF(1+R1/R2)
- 参考答案:C
- 您的答案:
参考解析:
W78XX的2、3端口额定输出电压为UREF,利用运算放大器的“虚短”概念,则UA+=UA-=U23=UR1。R1两端的电压等于UREF,通过关系计算可得:U0/(R1+R2)=UREF/R1,因此,U0=UREF(1+R2/R1)。
74LS161的功能如表所示,图示电路的分频比(即Y与CP的频率之比)为( )。
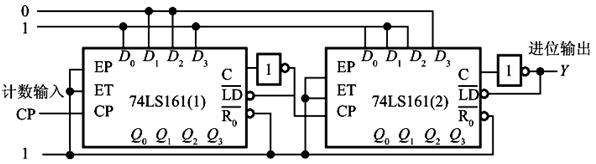

- A 1:63
- B 1:60
- C 1:96
- D 1:256
- 参考答案:A
- 您的答案:
参考解析:
74161为4位二进制异步计数器,可预置数的加法器。采用两片74161串行级联的方式,其中左片为低位计数,预置数为:(1001)2=(9)16=(9)10;右片为高位计数,预置数为:(0111)2=(7)16=(7)10。左片计数器从9开始计数,右片计数器从7开始计数,因此CP为:Y=(16-9)×(16-7)=63。
一台并网运行的三相同步发电机,运行时输出cosφ=0.5(滞后)的额定电流,现在要让它输出cosφ=0.8(滞后)的额定电流,可采取的办法是( )。
- A 输入的有功功率不变,增大励磁电流
- B 增大输入的有功功率,减小励磁电流
- C 增大输入的有功功率,增大励磁电流
- D 减小输入的有功功率,增大励磁电流
- 参考答案:B
- 您的答案:
参考解析:
由于电机额定电流是固定不变的,设为IN,忽略损耗,且电机输入有功功率等于输出有功功率,P=UNINcosφN。题解图为额定电流与励磁电流的关系,从图中可以看出,将cosφ=0.5变为cosφ=0.8,可减小励磁电流,但同时额定电流也减小,则为了使额定电流不变,可增大输入的有功功率。

一台隐极式同步发电机,忽略电枢电阻,同步电抗的标幺值XS*=1.0,端电压U保持额定值不变,当负载电流为额定值且功率因数为1,功率角δ为( )。
- A 0°
- B 36.87°
- C 45°
- D 90°
- 参考答案:C
- 您的答案:
参考解析:

每相同步电抗XS=1的三相隐极式同步发电机单机运行,供给每相阻抗标幺值为ZL=(8-j6)的三相对称负载,其电枢反应的性质为( )。
- A 纯交轴电枢反应
- B 直轴去磁兼交轴电枢反应
- C 直轴加磁兼交轴电枢反应
- D 纯直轴去磁电枢反应
- 参考答案:C
- 您的答案:
参考解析:
设同步发电机每相励磁电动势为E0∠0°,则电枢电流为:
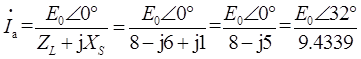
则同步发电机的内功率因数角ψ=-32°。则当时-90°<ψ<0°为直轴加磁兼交轴电枢反应。
设有两台三相变压器并联运行,额定电压均为6300/400V,联结组相同,其中A变压器额定容量为500kVA,阻抗电压UkA=0.0568;B变压器额定容量为1000kVA,阻抗电压UkB=0.0532,在不使任何一台变压器过载的情况下,两台变压器并联运行所能供给的最大负荷为( )。
- A 1200kVA
- B 1468.31kVA
- C 1500kvA
- D 1567.67kVA
- 参考答案:B
- 您的答案:
参考解析:
对于仅短路阻抗电压不同的变压器并联时,其并联运行变压器的负载系数与短路阻抗(短路电压)模值标幺值成反比。设A、B变压器负荷率分别为βA和βB,则有:βA/βB=UkB%/UkA%=0.0532/0.0568=0.9366。
在保证两台变压器都不过载的情况下,两变压器的最大负荷率分别为βA=0.9366和βB=1.0。则最大负荷为:S=SAβA+SBβB=500×0.9366+1000=1468.31kVA。
三相鼠笼式电动机,PN=10kW,UN=380V,nN=1455r/min,定子Δ接法,等效电路参数如下:R1=1.375Ω,R2′=1.04711,X1σ=2.43Ω,X2σ′=4.4Ω,则最大电磁转矩的转速为( )。
- A 1455r/min
- B 1275r/min
- C 1260r/min
- D 1250r/min
- 参考答案:B
- 您的答案:
参考解析:
当电磁转矩为最大值Tmax时,转差率为临界转差率Sm,则:
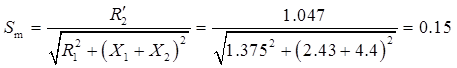
由于额定转速应与同步转速相差不大,因此同步转速n1=60f/p=60×50/2=1500r/min,故最大电磁转矩时电动机的转速为:n=(1-Sm)n1=(1-0.15)×1500=1275r/min。
电力系统的主要元件有( )。
- A 发电厂、变电所、电容器、变压器
- B 发电厂、变电所、输电线路、负荷
- C 发电厂、变压器、输电线路、负荷
- D 发电厂、变压器、电容器、输电线路
- 参考答案:B
- 您的答案:
参考解析:
电力系统由发电、输电、变电、配电和用电等环节组成,主要包括发电厂、变电所、输电线路、负荷。
电力系统电压降落计算公式为( )。
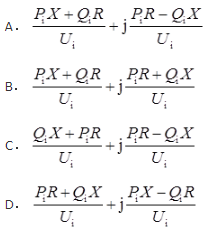
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
电压降落是指线路首末两端电压的相量差,是一个矢量,其公式为:
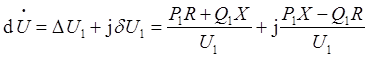
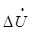 和
和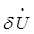 分别表示电压降的纵分量和横分量。
分别表示电压降的纵分量和横分量。
三相感应电动机定子绕组,Δ接法,接在三相对称交流电源上,如果有一相断线,在气隙中产生的基波合成磁势为( )。
- A 不能产生磁势
- B 圆形旋转磁势
- C 椭圆形旋转磁势
- D 脉振磁势
- 参考答案:C
- 您的答案:
参考解析:
设C相绕组断线,则C相电流为零,A、B两相仍流过对称两相电流。设A、B两项电流分别为:iA=Imsinωt,iB=Imsin(ωt-2π/3),坐标原点取A相绕组轴线上,则有:
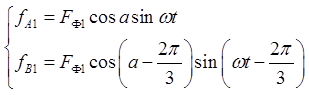
则f1=fA1+fB1=FΦ1[sin(ωt-a)-1/2sin(ωt+a-π/3)],因此,该气隙产生椭圆形磁动势。
简单系统如图所示,输电端母线A电压保持116kV,变压器低压母线C要求恒调压,电压保持10.5kV,满足以上要求时接在母线上的电容器容量Q为( )。

- A 8.76Mvar
- B 8.44Mvar
- C 9.76Mvar
- D 9.69Mvar
- 参考答案:B
- 您的答案:
参考解析:
线路与变压器参数计算如下:线路的电阻R=100×0.27=27Ω,电抗X=100×0.4=40Ω;变压器XT=0.105×110^2×10^3/30×10^3=42.35Ω;线路加变压器等效阻抗Z=27+j82.35Ω。
直接用末端功率计算网络电压损耗:U2max′=116-ΔUmax=116-(PR+QX)/U=116-(21×27+14×82.35)/116=101.17kV,U2min′=116-ΔUmin=116-(PR+QX)/U=116-(21×27+7×82.35)/116=108.7kV。根据调压要求,按最小负荷没有补偿的情况下确定变压器分接头:UT=U2min′×U2N/U2=108.7×11/10.5=113.88kV。选择最近的分接头为:110×(1+2.5%)=112.75kV,变比k=10.25。按照最大负荷来进行补充,则有:
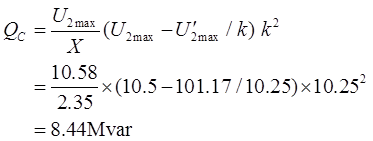
同步补偿机实际是特殊状态下的同步电动机,特殊状态是( )。
- A 满载运行
- B 空载运行
- C 短路堵转运行
- D 半载运行
- 参考答案:B
- 您的答案:
参考解析:
同步补偿机实质上就是同步电动机的空载运行,是专门的无功功率发电机,它也可以像同步电动机一样通过调节励磁电流来改变吸收无功的大小和无功的性质,其损耗由电网来提供。
系统发生三相短路后,其短路点冲击电流和最大有效值电流计算公式为( )。
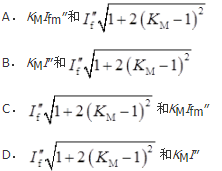
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
短路全电流峰值(冲击电流)出现在短路发生后的半个周期内即0.01秒瞬间,计算公式为: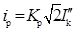 。短路全电流最大有效值IP公式为:
。短路全电流最大有效值IP公式为: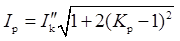 。式中,Kp为短路电流峰值系数,Kp=1+e-0.01/Tf;Tf为短路电流直流分量衰减时间常数,单位为s,当电网频率为50Hz时,Tf=XΣ/(314RΣ);X∑为短路电路总电抗,单位为Ω;R∑为短路电路总电阻,单位为Ω。
。式中,Kp为短路电流峰值系数,Kp=1+e-0.01/Tf;Tf为短路电流直流分量衰减时间常数,单位为s,当电网频率为50Hz时,Tf=XΣ/(314RΣ);X∑为短路电路总电抗,单位为Ω;R∑为短路电路总电阻,单位为Ω。
已知某电力系统如图所示,各线路电抗约为0.4Ω/km,长度标在图中,取SB=250MVA,如果厂处发生三相短路时,其短路电流周期分量起始值及冲击电流分别为( )。
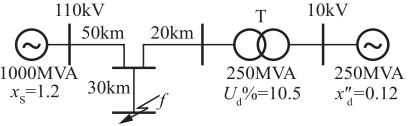
- A 0.29,2.395
- B 2.7,6.82
- C 0.21,2.395
- D 2.1,6.82
- 参考答案:B
- 您的答案:
参考解析:

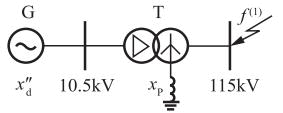
系统如图所示,系统中各元件在统一基准功率下的标幺值阻抗:G:x″d=x(2)=0.03,x(0)=0.15,E=1.12;T:xT=0.06,Y/Δ—11接法,中性点接地阻抗xp=0.04/3,当图示f点发生A相接地短路时,短路处A相短路电流和电路点处系统的等值零序电抗分别为( )。
- A 12,0.1
- B 4,0.1
- C 0.09,4
- D 12,0.04
- 参考答案:A
- 您的答案:
参考解析:
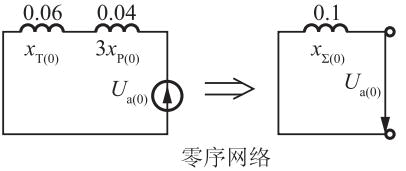
正(负)序网络图如题解图(a)所示。则正、负序网络等值电抗为:x∑(1)=x∑(2)=0.03+0.06=0.09。零序电流仅在变压器中流通,零序序网如题解图(b)所示。则零序网络等值电抗为:x*∑(0)=0.06+3×0.04/3=0.1。因此,短路电流标幺值为:
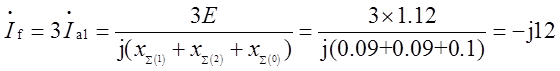
题解图(a)
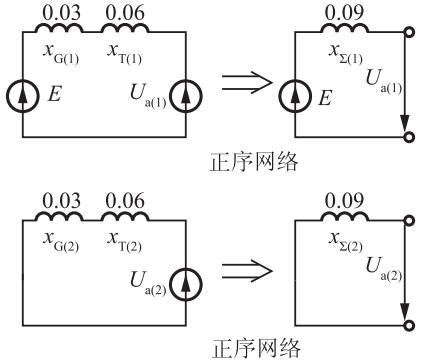
题解图(b)
下列哪种主接线在出线断路器检修时,会暂时中断该回路的供电( )
- A 三分之四
- B 双母线分段
- C 二分之三
- D 双母线分段带旁路
- 参考答案:B
- 您的答案:
参考解析:
双母线分段接线的优点包括:①轮换检修母线而不致中断供电;②检修任一回路的母线隔离开关时仅使该回路停电;③工作母线发生故障时,经倒闸操作这一段停电时间后可迅速恢复供电;④检修任一回路断路器时,可用母联断路器来代替,不致使该回路的供电长期中断。AC两项,二分之三断路器及三分之四断路器接线运行灵活性好,可靠性高,任一组母线故障,不会停电;D项,双母线带旁路母线接线检修任一进出线的断路器时,经由旁路断路器及相应线路上的旁路隔离开关,不必中断供电。
电流互感器的容量为( )。
- A 正常发热允许的容量
- B 短路发热允许的容量
- C 额定二次负载下的容量
- D 额定二次电流下的容量
- 参考答案:C
- 您的答案:
参考解析:
电流互感器的容量可用二次负荷与额定二次电流表示,关系为:Sb=ZbI2sn。电流互感器的二次侧额定电流一般有1A和5A两种,而其负荷通常由两部分组成,一部分是所连接的测量仪表或保护装置,另一部分是连接导线。
断路器开断中性点不直接接地系统中的三相短路电流,首先开断相后的工频恢复电压为(Uph为相电压)( )。
- A Uph
- B 0.866Uph
- C 1.5Uph
- D 1.3Uph
- 参考答案:C
- 您的答案:
参考解析:
三相断路器在开断短路故障时,由于动作的不同期性,首相开断的断口触头间所承受的工频恢复电压将要增高,增高的数值用首相开断系数来表征。首相开断系数是指三相系统当两相短路时,在断路器安装处的完好相对另两相间的工频电压与短路去掉后在同一处获得的相对中性点电压之比。题55解图分析系统中经常发生的各种短路形式,首先开断相断口间的工频恢复电压,中性点不接地系统者多为1.5倍的相电压;中性点接地系统多为1.3倍相电压。中性点不直接接地系统的三相短路故障如图所所示:
设A相为首先开断相:电弧电流先过零,电弧先熄灭,即:
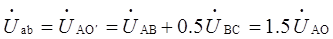
在A相熄灭后,经过5ms(90°),B、C两相电流同时过零,电弧同时熄灭,此时电源的线电压加在两个串联的断口上,若认为两断口是均匀分布,则每一断口只承担一半电压,即0.5UBC=0.866UBO(UCO)。