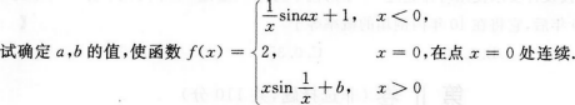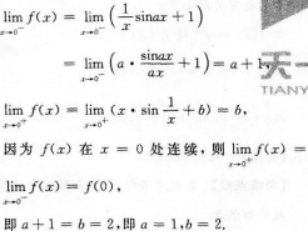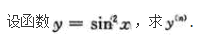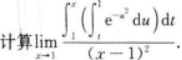下列反常积分发散的是( )。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:

把两封信随机地投入标号为1,2,3,4的4个邮筒中,则1,2号邮筒各有一封信的概率等于
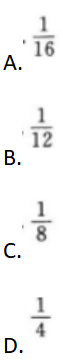
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题考查了古典概率的知识点.【应试指导】因两封信投向四个邮筒共有的投法(可重复排列)为n=42=16;满足1,2号邮筒各有一封信的投法为
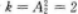
,故所求概率为
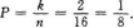
下列反常积分收敛的是()

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了反常积分的敛散性的知识点.【应试指导】
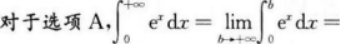

当x→0时,无穷小量x+sinx是比x的()
- A 高阶无穷小
- B 低阶无穷小
- C 同阶但非等价无穷小
- D 等价无穷小
- 参考答案:C
- 您的答案:
参考解析:
本题考查了无穷小量的知识点.
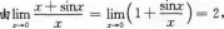
所以x→0时,2+sinx与x是同阶但非等价无穷小.
曲线y=x3-3x上切线平行于x轴的点是()
- A (0,0)
- B (1,2)
- C (-1,2)
- D (-1,-2)
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题考查了曲线上一点处的切线的知识点.【应试指导】由y=x3-3x得y'=3x2-3,令y'=0,得x=±1.经计算x=-1时,y=2;x=1时,y=-2,故选C.
下列极限计算正确的是()
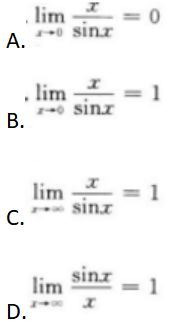
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
本题考查了极限的知识点.

函数y=|x|+1在x=0处()
- A 无定义
- B 不连续
- C 连续但是不可导
- D 可导
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题考查了函数在一点可导、连续的性质的知识点.【应试指导】从四个选项的内容来看,我们可以一步一步地处理,x=0时,y=1,

下列极限等于1的是()
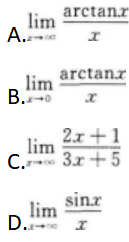
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了极限的知识点.【应试指导】
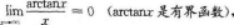

函数f(x)=x4-24x2+6x在定义域内的凸区间是()
- A (-∞,0)
- B (-2,2)
- C (0,+∞)
- D (-∞,+∞)
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了函数的凸区间的知识点.【应试指导】因为f(x)=x4-24x2+6x,则f'(x)=4x3-48x+6,f”(x)=12x2-48=12(x2-4),令f''(x)<0,有x2-4<0,于是-2
当x→0时,下列变量是无穷小量的是()
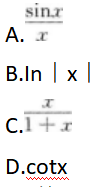
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题考查了无穷小量的知识点.【应试指导】经实际计算及无穷小量定义知应选C

把A排除,再利用Inx的性质可把B排除,C自然可验证是正确的,由Cotx的性质,可排除D项.
若f(u)可导,且y=f(ex),则dy=()
- A f'(ex)dx
- B f'(ex)exdx
- C f(ex)exdx
- D f'(ex)
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了复合函数的微分的知识点.【应试指导】因为y=f(ex),所以,y'=f'(ex)exdx.
如果在区间(a,b)内,函数f(x)满足f′(x)>0,f′′(x)<0,则函数在此区间是()
- A 单调递增且曲线为凹的
- B 单调递减且曲线为凸的
- C 单调递增且曲线为凸的
- D 单调递减且曲线为凹的
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题考查了函数的单调性和凹凸性的知识点.【应试指导】因f'(x)>0,故函数单调递增,又f''(x)<0.所以函数曲线为凸的.
曲线y=(x-1)3-1的拐点是()
- A (2,0)
- B (1,-1)
- C (0,-2)
- D 不存在
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了曲线的拐点的知识点.【应试指导】因y=(x-1)3-1,y'=3(x-1)2,y''=6(x-1).令y''=0得x=1,当x<1时,曲线 有拐点(1,-1).
有拐点(1,-1).
设z=xy,则dz=()
- A yxy-1dx+xyInxdy
- B xy-1dx+ydy
- C xy(dx+dy)
- D xy(xdx+ydy)
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题考查了二元函数的全微分的知识点【应试指导】
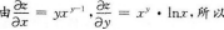
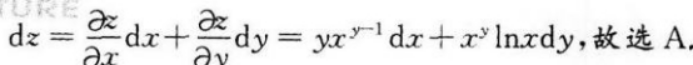
某建筑物按设计要求使用寿命超过50年的概率为0.8,超过60年的概率为0.6,该建筑物经历了50年后,它将在10年内倒塌的概率等于()
- A 0.25
- B 0.30
- C 0.35
- D 0.40
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题考查了条件概率的知识点.【应试指导】设A={该建筑物使用寿命超过50年},B={该建筑物使用寿命超过60年}由题意,P(A)=0.8,P(B)=0.6,所求概率为:
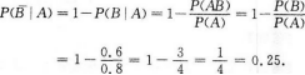
对于函数z=xy,原点(0,0)()
- A 不是函数的驻点
- B 是驻点不是极值点
- C 是驻点也是极值点
- D 无法判定是否为极值点
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了函数的驻点、极值点的知识点.

函数f(x)=x4-24x2+6x在定义域内的凸区间是()
- A (-,0)
- B (一2,2)
- C (0,+)
- D (-,)
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了函数的凸区间的知识点.
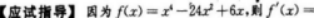
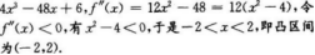
设y=xn,n为正整数,则y(n)=()
- A 0
- B 1
- C n
- D n!
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了一元函数的高阶导数的知识点.
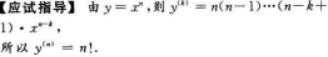
下列四个函数不能做随机变量x的分布函数的是()
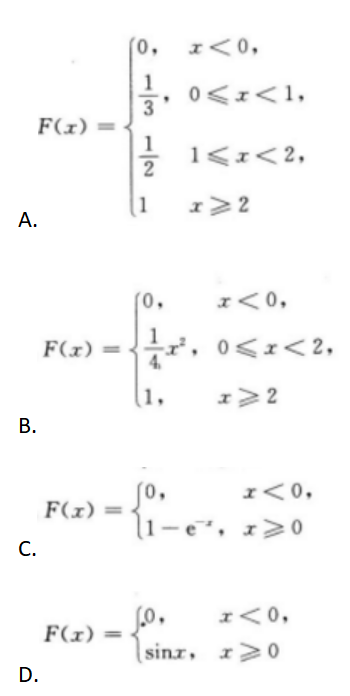
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了分布函数的知识点.
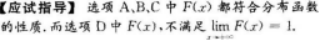
设F(z)是f(z)的一个原函数,则∫cosxf(sinx)dx=( )
- A F(cos)+C
- B F(sinx)+
- C -F(cosx)+C
- D -F(sinx)+C
- 参考答案:B
- 您的答案:
参考解析:
本题考查了不定积分的换元积分法的知识点.
∫Cosf(sinx)dx
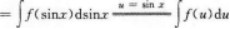
=F(u)+C=F(sinx)+C.
设f(x)在[a,b]上连续,且a≠-b,则下列各式不成立的是( )
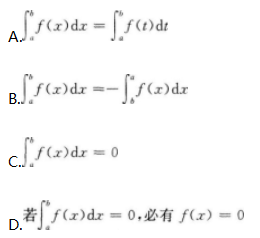
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
本题考查了定积分的相关知识的知识点.
由题意知,C项不成立,其余各项均成立.
甲、乙两人独立地对同一目标射击一次,其命中率分别为0.6和0.5,现已知目标被命中,是甲射中的概率为( )
- A 0.6
- B 0.75
- C 0.85
- D 0.9
- 参考答案:B
- 您的答案:
参考解析:
本题考查了条件概率的知识点.
设A1={甲射中目标),A2={乙射中目标),B=(目标被命中).由题意,P(A1)=0.6,P(A2)=0.5,B=A1UA2,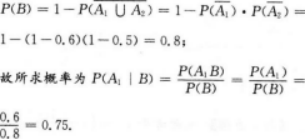
用A表示事件“甲考核通过且乙考核不通过”,则其对立事件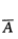 为( )
为( )
- A “甲考核不通过,乙考核通过”
- B “甲、乙考核都通过”
- C “甲考核不通过”
- D “甲考核不通过或乙考核通过”
- 参考答案:D
- 您的答案:
参考解析:
若随机事件A与B相互独立,而且P(A)=0.4,P(B)=0.5,则P(AB)=( )
- A 0.2
- B 0.4
- C 0.5
- D 0.9
- 参考答案:A
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:

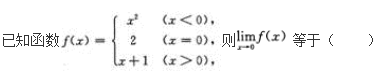
- A 1
- B 0
- C 2
- D 不存在
- 参考答案:D
- 您的答案:
参考解析:
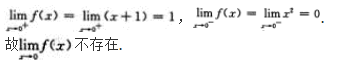

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
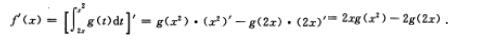

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
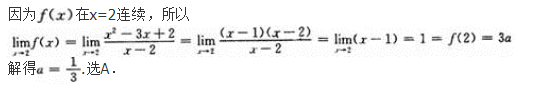

- A (-∞,-2)和(-2,+∞)
- B (-2,2)
- C (-∞,0)和(0,+∞)
- D (-2,0)和(0,2)
- 参考答案:D
- 您的答案:
参考解析:


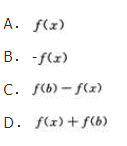
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:

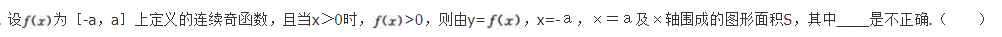

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
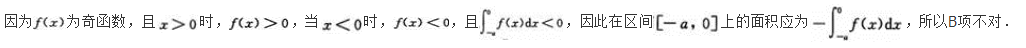


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
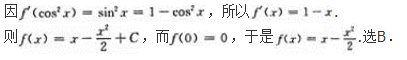

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
本题考查了利用导数定义求极限的知识点.
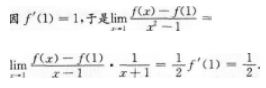


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
本题考查了不定积分的知识点.【考情点拨】本题考查了不定积分的知识点.

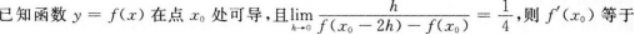
- A -4
- B -2
- C 2
- D 4
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了利用定义求函数的一阶导数的知识点.【应试指导】
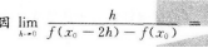
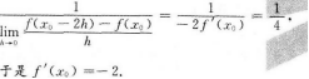

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
本题考查了已知导函数求原函数的知识点.
因f'(Cos2x)=sin2x-1-Cos2x,于是f'(x)=1-x,两边积分得f(x)=x-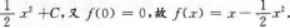
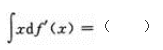
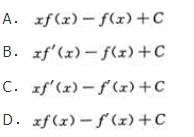
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
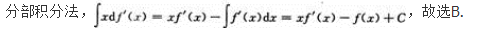
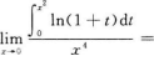
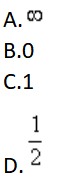
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了极限(洛必达法则)的知识点.
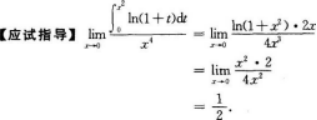
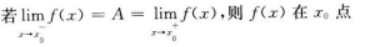
- A 一定有定义
- B 一定有f(x0)=A
- C 一定连续
- D 极限一定存在
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了极限的知识点.

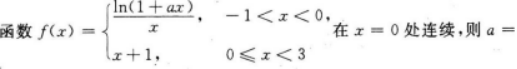
- A 1
- B 2
- C 3
- D 4
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题考查了函数在一点处连续的知识点.【应试指导】f(x)在x=0处连续,所以f(x)在x=0处左连续、右连续,
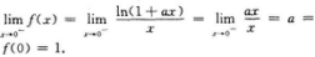
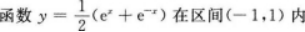
- A 单调减少
- B 单调增加
- C 不增不减
- D 有增有减
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了函数的单调性的知识点.【应试指导】因为y=, 令y'=0,得x=0;当x>0时.y'>0;当x<0时,y’<0,故在(-1,1)内,函数有增有减.
令y'=0,得x=0;当x>0时.y'>0;当x<0时,y’<0,故在(-1,1)内,函数有增有减.
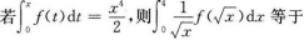
- A 2
- B 4
- C 8
- D 16
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了定积分的换元积分法的知识点.【应试指导】解法1:
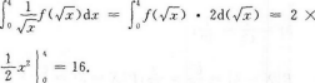
解法2:
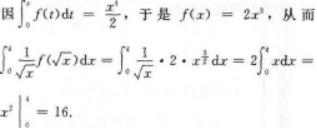
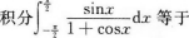
- A -1
- B 0
- C 1
- D 2
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了定积分的知识点.【应试指导】解法1:

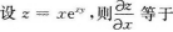
- A xyexy
- B x2exy
- C exy
- D (1+xy)exy
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了二元函数的一阶偏导数的知识点.【应试指导】
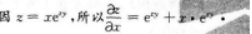
y=(1+xy)exy
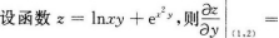
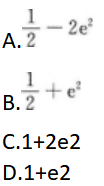
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了二元函数的一点处的一阶偏导数的知识点.【应试指导】

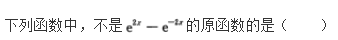
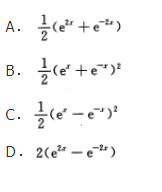
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
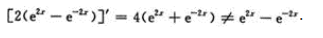
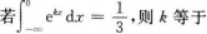
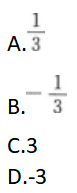
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题考查了无穷区间的反常积分的知识点.【应试指导】


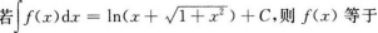
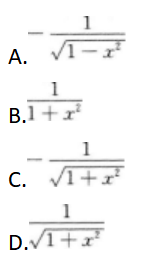
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题考查了不定积分的知识点.【应试指导】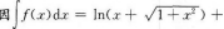
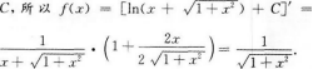
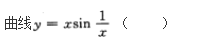
- A 仅有水平渐近线
- B 既有水平渐近线又有铅直渐近线
- C 仅有铅直渐近线
- D 既无水平渐近线又无铅直渐近线
- 参考答案:A
- 您的答案:
参考解析:
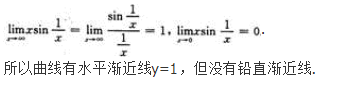

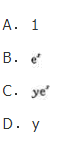
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
新版章节练习,考前压卷,完整优质题库+考生笔记分享,实时更新,用软件考,

- A F(cosx)+C
- B F(sinx)+
- C -F(cosx)+C
- D -F(sinx)+C
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题考查了不定积分的换元积分法的知识点.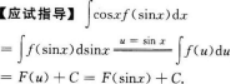
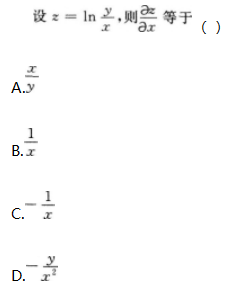
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
本题考查了二元函数的一阶偏导数的知识点.


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

- A (1,0)
- B (1,2)
- C (-3,0)
- D (-3,2)
- 参考答案:A
- 您的答案:
参考解析:

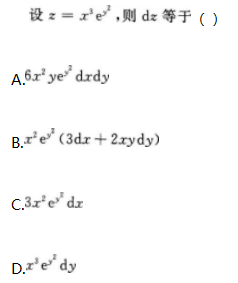
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
本题考查了二元函数的全微分的知识点.
新版章节练习,考前压卷,完整优质题库+考生笔记分享,实时更新,用软件考,
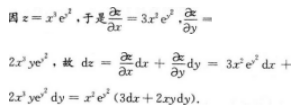

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
一批零件中有10个合格品,3个次品,安装机器时,从这批零件中任取一个,取到合格品才能安装.若取出的是次品,则不再放回,求在取得合格品前已取出的次品数X的概率分布.
一个袋子中有5个球,编号为1,2,3,4,5,同时从中任取3个,以X表示取出的3个球中的最大号码,求随机变量X的概率分布.
曲线x2+y2=2x在点(1,1)处的切线方程为.
曲线y=x3-3x2+2x+1的拐点是
- 参考答案:
- 您的答案:
参考解析:
.【答案】(1,1)【考情点拨】本题考查了曲线的拐点的知识点.
【应试指导】y'=3x2-6x+2,y''=6x-6,令y''=0,得x=1.则当x>1时,y''>0;当x<1时,y''<0.又因x=1时y=1,故点(1,1)是拐点(因y=x3-3x2+2x+1在(-∞,+∞)上处处有二阶导数,故没有其他形式的拐点).
∫sin2xCosxdx=.
求y=f(x)=2x3-3x2-12x+14的极值点和极值,以及函数曲线的凸凹性区间和拐点.
- 参考答案:
- 您的答案:
参考解析:
y'=6x2-6x-12,y''=12x-6,令y'=0得驻点x1=-1,x2=2,当x2=2时,y''=18>0.所以f(z)在x=2处取极小值-6.当x1=-1时,y''<0.所以f(x)在x=-1处取极大值21.
当x>0时,证明:ex>1+x.
- 参考答案:
- 您的答案:
参考解析:
证法1:在[0,x]上令F(x)=ex,则使用拉格朗日定理得,F(x)-F(0)=F'(ξ)(x-0),ξ∈(0,x),即ex-1=eξ·x,由于eξ>1.所以ex-1>x,即ex>1+x.证法2:令G(x)=ex-1-x,则G'(x)=ex-1,故在[0,x]内G'(x)>0,所以在[0,x]上G(x)单调递增,由G(0)=0,得x>0时,G(x)>0,即ex-1-x>0,亦即ex>1+x.
设y=x2cosx+2x+e,则y′=.
- 参考答案:
- 您的答案:
参考解析:
【答案】2xcosx-x2sinx+2xIn2【考情点拨】本题考查了一元函数的一阶导数的知识点.
【应试指导】(x2cosx)'=2xcosx-x2sinx,(2x)'=2x·In2,e'=0。所以y'=2xcosx-x2sinx+2xIn2.
从一批有10件正品及2件次品的产品中,不放回地一件一件地抽取产品,设每个产品被抽到的可能性相同,求直到取出正品为止所需抽取的次数X的概率分布。
确定函数y=2x4-12x2的单调区间、极值及函数曲线的凸凹性区间和拐点.
- 参考答案:
- 您的答案:
参考解析:

又应当-∞
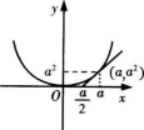
设曲线y=x2+x-2在点M处切线的斜率为2,则点M的坐标为().
电路由两个并联电池A与B,再与电池C串联而成,设电池A、B、C损坏的概率分别是0.2,0.2,0.3,求电路发生间断的概率.
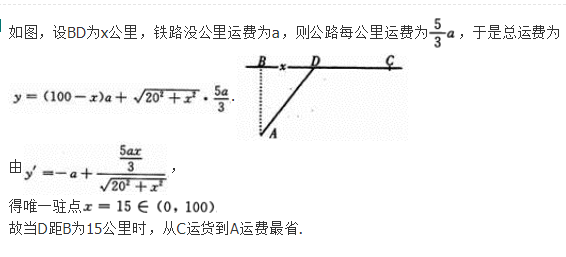
设工厂A到铁路线距离为20公里,垂足为B,铁路线上距离B为100公里处有一原料供应站C,现从BC间某处D向工厂A修一条公路,为使从C运货到A运费最省,问D应选在何处?(已知每公里铁路与公路运费之比为3:5)
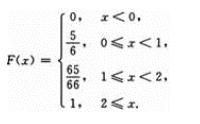
一批零件中有10个合格品和2个废品,安装机器时,从这批零件中任取一个,如果每次取出废品后不再放回,用X表示在取得合格品以前已取出的废品数,求:
1.随机变量X的分布列;
2.随机变量X的分布函数.
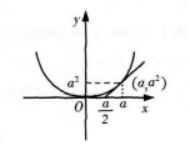
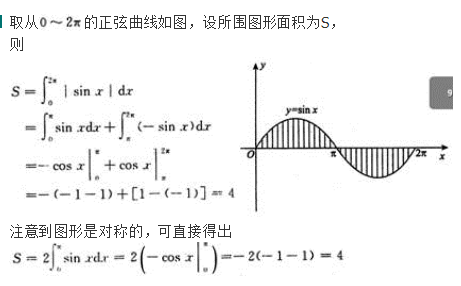
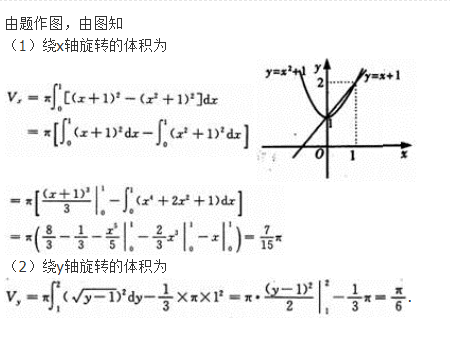
(1)求在区间[0,π]上的曲线y=sinx与x轴所围成图形的面积S.
(2)求(1)中的平面图形绕x轴旋转一周所得旋转体的体积V.
设f(x)是[-2,2]上的偶函数,且f′(-1)=3,则f′(1).
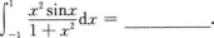

- 参考答案:
- 您的答案:
参考解析:
【答案】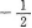 【考情点拨】本题考查了隐函数在一点处的一阶导数的知识点.
【考情点拨】本题考查了隐函数在一点处的一阶导数的知识点.
【应试指导】x2+2xy-y2=2x两边对x求导(注意y是z的函数),因2x+2y+2xy’-2yy’=2,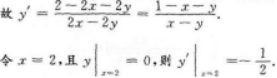


- 参考答案:
- 您的答案:
参考解析:
【答案】-2xysin(xy2)【考情点拨】本题考查了二元函数的一阶偏导数的知识点.
【应试指导】
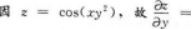 -sin(xy2)·(xy2)'=-2xysin(xy2).
-sin(xy2)·(xy2)'=-2xysin(xy2).
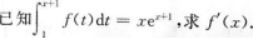


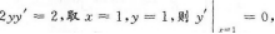
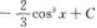 【考情点拨】本题考查了不定积分的知识点
【考情点拨】本题考查了不定积分的知识点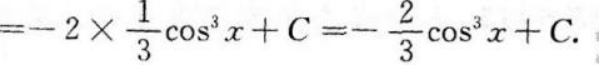
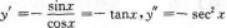 所以y''(0)=-1.
所以y''(0)=-1.

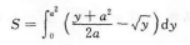
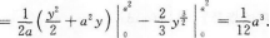

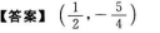
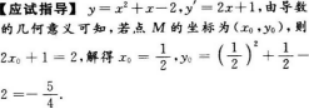

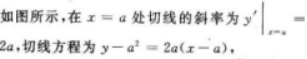
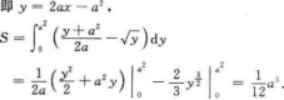



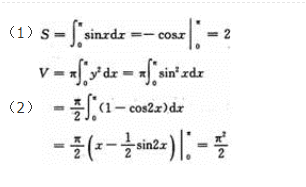
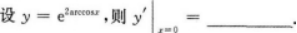

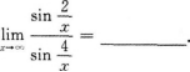


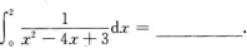
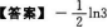

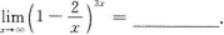
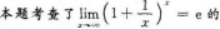 应用的知识点.
应用的知识点.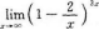
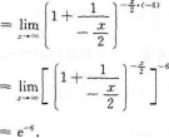
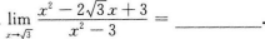
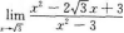
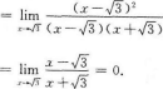
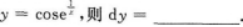
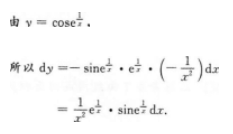
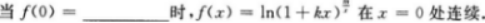
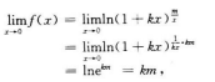
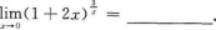
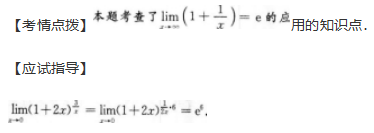
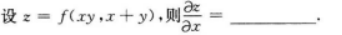
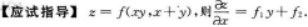
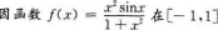
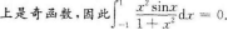
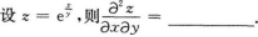
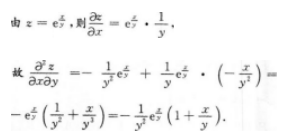
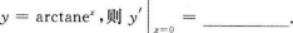
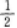 【考情点拨】本题考查了一元函数在一点处的一阶导数的知识点.
【考情点拨】本题考查了一元函数在一点处的一阶导数的知识点.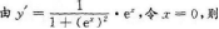

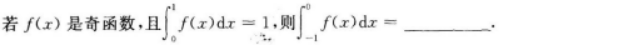
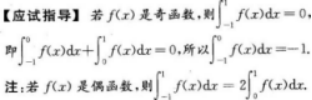
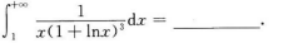
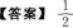

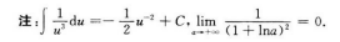
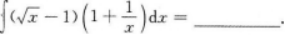
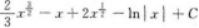 【考情点拨】本题考查了不定积分的知识点.
【考情点拨】本题考查了不定积分的知识点.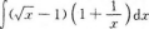
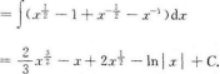
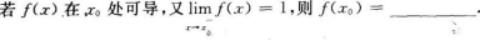

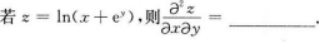
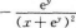 【考情点拨】本题考查了二元函数的混合偏导数的知识点.
【考情点拨】本题考查了二元函数的混合偏导数的知识点.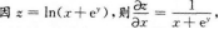
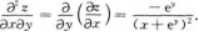
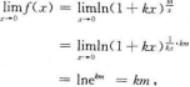

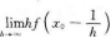


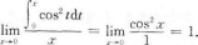
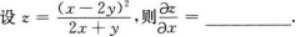
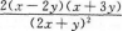 【考情点拨】本题考查了二元函数的一阶偏导数的知识点.
【考情点拨】本题考查了二元函数的一阶偏导数的知识点.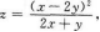
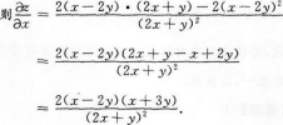
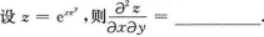
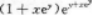 【考情点拨】本题考查了二元函数的混合偏导数的知识点.
【考情点拨】本题考查了二元函数的混合偏导数的知识点.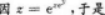
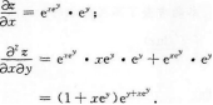
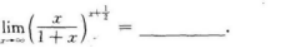
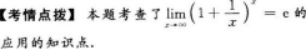
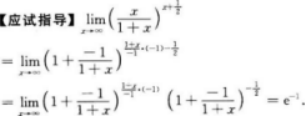
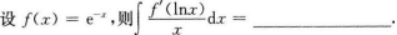
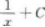 【考情点拨】本题考查了不定积分的知识点.
【考情点拨】本题考查了不定积分的知识点.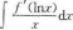
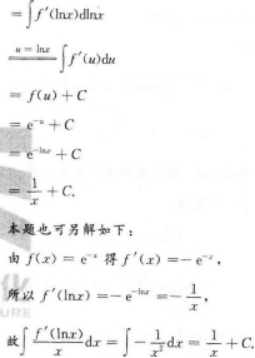
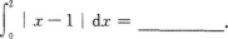
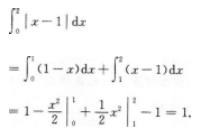
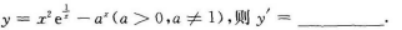
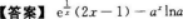
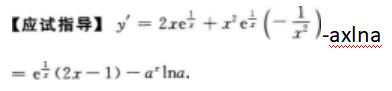
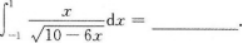
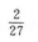 【考情点拨】本题考查了定积分的知识点.
【考情点拨】本题考查了定积分的知识点.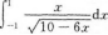
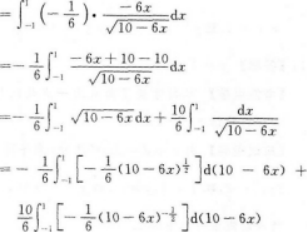


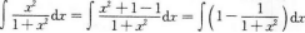
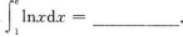
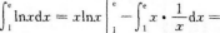

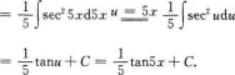

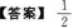


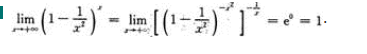

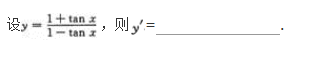

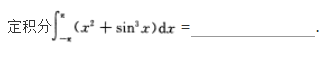
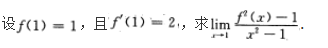

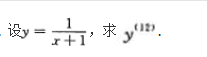

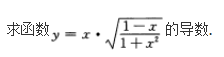

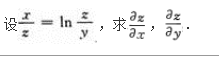

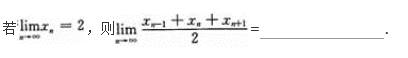

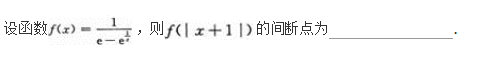


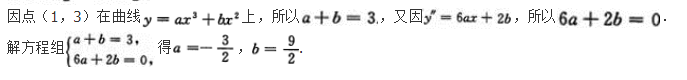




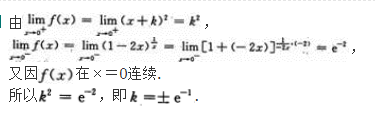



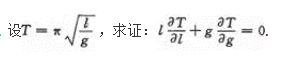

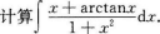



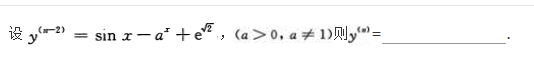
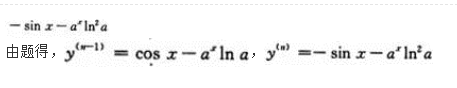
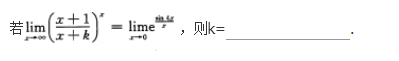
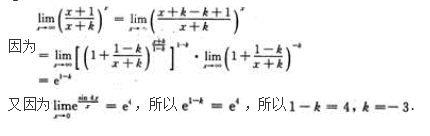
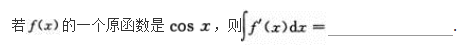
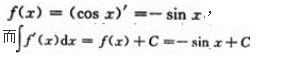
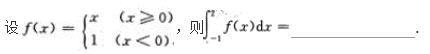
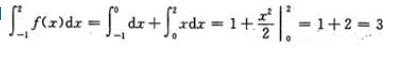
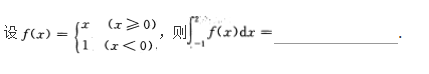
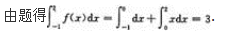
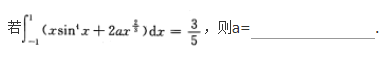
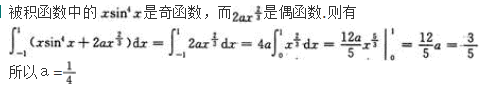
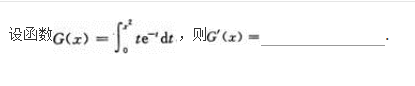
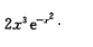
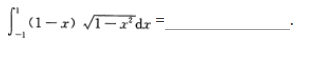
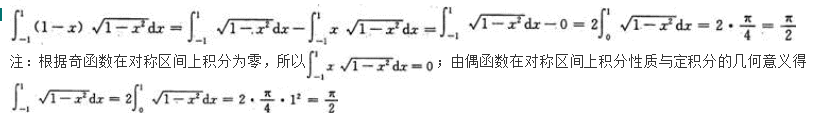
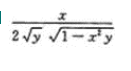
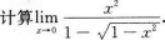
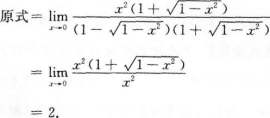 注:本题也可用洛必达法则求解.
注:本题也可用洛必达法则求解.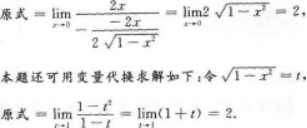
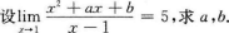

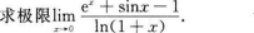
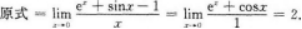
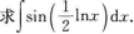
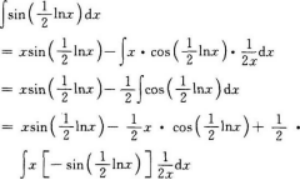
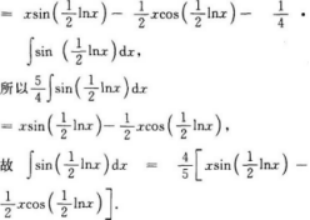
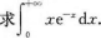
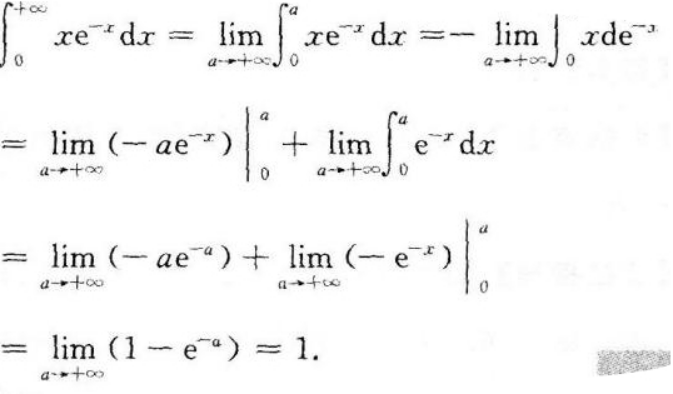
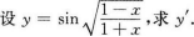



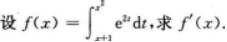
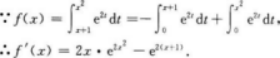
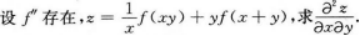
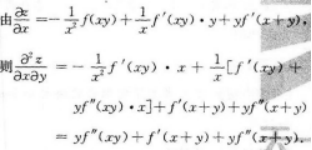
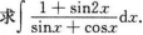
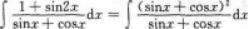 =∫(sinx+Cosx)dx
=∫(sinx+Cosx)dx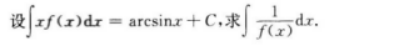

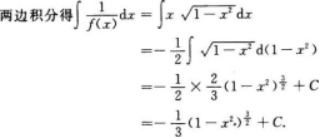
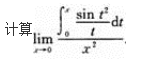
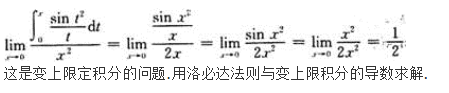
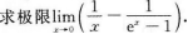

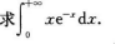
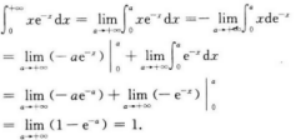
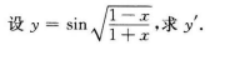
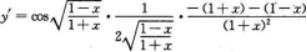
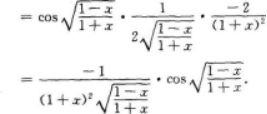
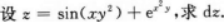
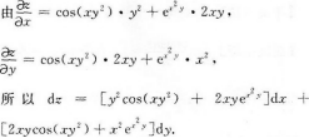
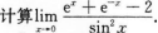
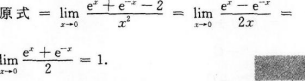 注:将分母sin2x用于之等价的无穷小量x2代
注:将分母sin2x用于之等价的无穷小量x2代