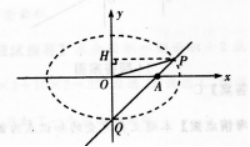
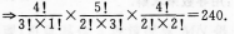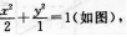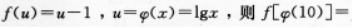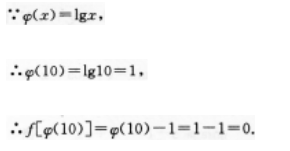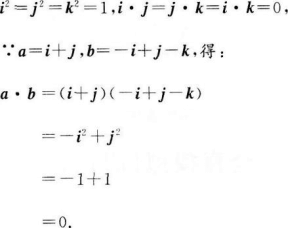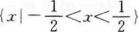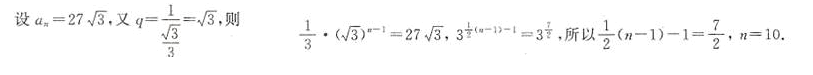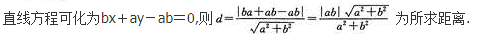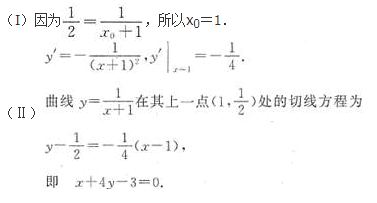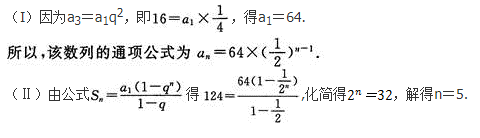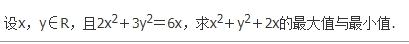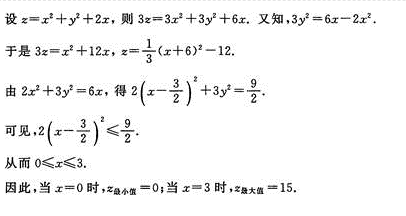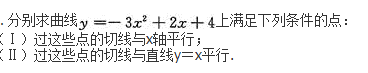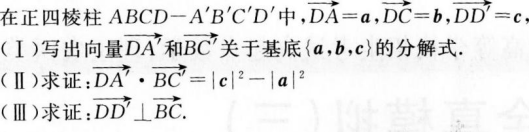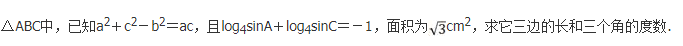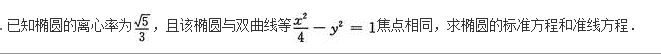设0
AP(A+B|< )=P(A|
)=P(A| )+P(B|
)+P(B| )
)
BP(AC+BC)=P(AC)+P(BC)
CP(A+B)=P(A|C)+P(B|C)
DP(C)=P(A)P(C|A)+P(B)P(C|A)
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
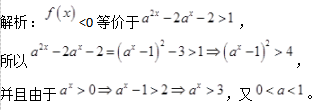
下列说法正确的是( )

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
直三棱柱的每个侧面的面积为5,底面积是10,全面积是( )
- A 15
- B 20
- C 25
- D 35
- 参考答案:D
- 您的答案:
参考解析:
本题主要考查的知识点为直三棱柱的全面积.
求全面积=侧面积+2底面积=5×3+10×2=35,应选D.误选C,错误的原因是只加了一个底面的面积.
已知偶函数y=f(x)在区间[a,b](0
- A 增函数
- B 减函数
- C 不是单调函数
- D 常数
- 参考答案:B
- 您的答案:
参考解析:
本题主要考查的知识点为偶函数的增减性.
由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0
∵y=f(x)为偶函数,
∴f(-a)=f(a).f(-b)=f(b),
又∵f(a)
∴f(-a)
∴f(x)在[-b,-a]上为减函数.
在△ABC中,若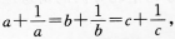 则△ABC必是( )
则△ABC必是( )
- A 直角三角形
- B 等腰三角形
- C 等边三角形
- D 钝角三角形
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为等式的变换. 【应试指导】
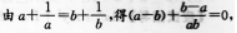
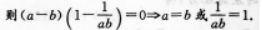
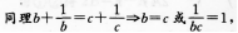
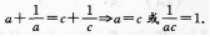
∴a=b=C.
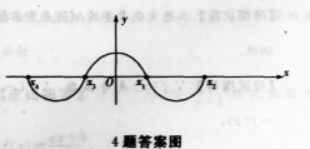
已知f(χ)是偶函数,且其图像与χ轴有4个交点,则方程f(χ)=0的所有实根之和为( )
- A 4
- B 2
- C 1
- D 0
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为偶函敷的性质. 【应试指导】设f(χ)=0的实根为
∵f(χ)为偶函数,
∴χ1,χ2,χ3,χ4,两两成对出现(如图),
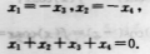
设全集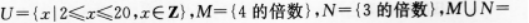 ( )
( )
- A {3,4,6,8,9,12,15,16,18,20}
- B {3}
- C <img src='http://tp.mxqe.com/data/876/14292795_0_1.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>
- D {3,5,7,11,13,17,19}
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为集合的运算. 【应试指导】

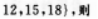
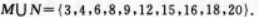
下列等式中,不成立的是( )
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为向量的运算. 【应试指导】对于选项A,用两向量相等的定义便知其错.
函数y=2χ的图像与函数χ=log2y的图像( )
- A 关于χ轴对称
- B 关于y轴对称
- C 关于直线y=χ对称
- D 是同一条曲线
- 参考答案:D
- 您的答案:
参考解析:

下列各式正确的是( )

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为三角函数的性质. 【应试指导】选项A错,

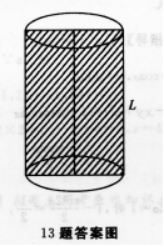
圆柱的轴截面面积等于10,体积为5π,它的母线长和侧面积分别是( )
- A 5和10π
- B 5π和10
- C 5和25π
- D 10和10π
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为圆柱的母线长和侧面积. 【应试指导】求母线的长,可从圆柱的截面积中求出.如图,

已知集合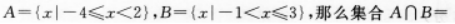 ( )
( )
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为集合的运算. 【应试指导】
设函数f(χ)在(-∞,+∞)上有定义,则下列函数中必为偶函数的是( )
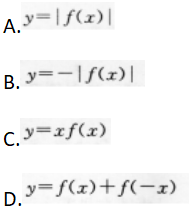
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为函数的奇偶性. 【应试指导】考查函数的奇偶性.只需将f(χ)中的χ换成-χ.计算出f(-χ).然后用奇函数.偶函数定义下结论.
对于A、B、C项无法判断其奇偶性.而选项D有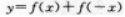 将f(χ)中的χ换写成-χ有
将f(χ)中的χ换写成-χ有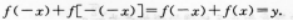
下列函数中,( )不是周期函数.
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为三角函数的周期性. 【应试指导】A是周期函数.B不是周期函数.C是周期函数.D是周期函数.
6名学生和l名教师站成一排照相,教师必须站在中间的站法有( )
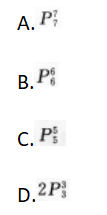
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为排列数. 【应试指导】此题是有条件限制的排列问题.让教师站在中间,6名学生的全排列有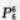 种.
种.
以χ2-3χ-1=0的两个根的平方为根的一元二次方程是( )
- A χ2-11χ+10
- B χ2+χ-11=0
- C χ2-11χ-1=0
- D χ2+χ+1=0
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为根与系数的关系. 【应试指导】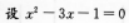 的两根分别为χ1,χ2,则由根与系数的关系得χ1+χ2=3,
的两根分别为χ1,χ2,则由根与系数的关系得χ1+χ2=3,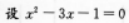
又所求方程的两根为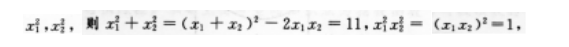
∴所求方程为χ2-11χ+1=0.
圆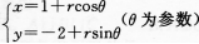 的圆心在( )点上.
的圆心在( )点上.
- A (1,-2)
- B (0,5)
- C (5,5)
- D (0,O)
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为圆的参数方程. 【应用指导】
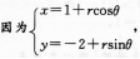
∴圆的圆心为O(1,-2).
过点P(5,0)与圆χ2+y2-4χ-5=0相切的直线方程是( )
- A y=5
- B χ=5
- C y=-5
- D χ=-5
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为圆的切线. 【应试指导】将圆的一般方程配方得出圆的标准方程.
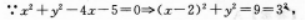
则点P(5,O)在圆上只有一条切线(如图),即χ=5.
某类灯泡使用时数在1000小时以上的概率为0.2,三个灯泡在使用1000小时以后最多只有一个坏的概率为( )
- A 0.008
- B 0.104
- C 0.096
- D 1
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为分类计数原理. 【应试指导】已知灯泡使用1000小时后好的概率为0.2,坏的概率为1-0.2=0.8,则三个灯泡使用1000小时以.后,可分别求得:
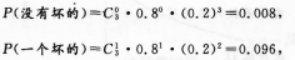
故最多只有一个坏的概率为:0.008+0.096=0.104.
设甲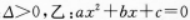 有两个不相等的实数根,则( )
有两个不相等的实数根,则( )
- A 甲是乙的必要条件,但不是充分条件
- B 甲是乙的充分条件,但不是必要条件
- C 甲是乙的充分必要条件
- D 甲不是乙的充分条件,也不是必要条件
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为简易逻辑. 【应试指导】 有两个不相等的实数根.
有两个不相等的实数根.
若函数y=f(χ)的定义域是[-1,1),那么f(2χ-1)的定义域是( )
- A [0,1)
- B [-3,1)
- C [-1,1)
- D [-1,0)
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为函数的定义域. 【应试指导】由已知,得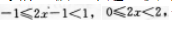 故求定义域为
故求定义域为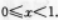
已知向量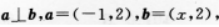 则χ=( )
则χ=( )
- A 4
- B -8
- C 8
- D -4
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为向量的垂直. 【应试指导】
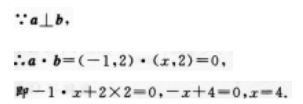
a,b是实数,a≠b,且ab≠0,方程bχ2+ay2=ab及y=aχ+b行表示的曲线只能是( )
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为直线与圆锥曲线的相交关系. 【应试指导】考查直线与圆锥曲线的相交关系时,应对它们的系数分四种情况讨论,做到不重复、不遗漏.

正方形边长为口,围成圆柱,体积为( )
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为圆柱的体积. 【应试指导】欲求圆柱的体积,由体积公式可知,必须知道圆柱的高(即正方形的边长)、半径,半径可由圆柱的周长等于正方形的边长求出。如图,
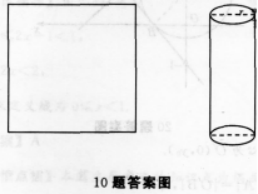
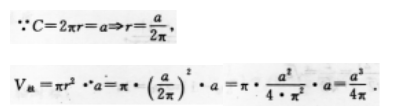
设A、B、C是三个随机事件,用A、B、C的运算关系( )表示事件:B、C都发生,而A不发生.
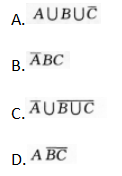
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为随机事件的表示. 【应试指导】选项A,表示A或B发生或C不发生.选项C,表示A不发生或B、C不发生.选项D,表示A发生且B、C不发生.
复数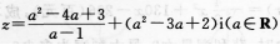 为实数,则a=( )
为实数,则a=( )
- A 1
- B 2
- C 3
- D 4
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为复数的概念. 【应试指导】由题意知,
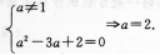
异面直线a,b所成的角60°,直线a⊥c,则直线b与c所成的角的范围为( )
- A [30°,90°]
- B [60°,90°]
- C [30°,60°]
- D [30°,120°]
- 参考答案:A
- 您的答案:
参考解析:

如果两个平面有3个公共点,则这两个平面( )
- A 重合
- B 只有3个公共点
- C 相交
- D 重合或相交
- 参考答案:D
- 您的答案:
参考解析:
如果两个平面的3个公共点不在同一条直线上,那么这两个平面重合;如果这3个公共点在同一条直线上,这两个平面相交或重合.
8名选手在有8条跑道的运动场进行百米赛跑,其中有2名中国选手。按随机抽签方法决定选手的跑道,2名中国选手在相邻的跑道的概率为( )
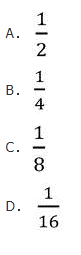
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:

已知椭圆的长轴长与短轴长的比为3∶4,则其离心率为( )
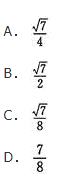
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
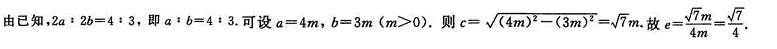
已知一个等差数列的第5项等于10,前3项的和等于3,那么这个等差数列的公差( )
- A 3
- B 1
- C -1
- D -3
- 参考答案:A
- 您的答案:
参考解析:
由题意知a5=a1+4d=10,S3=a1+a2+a3=3a1+3d=3,两式联立求得a1=-2,d=3.
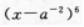 展开式中,末3项的系数(a,χ均未知)之和为( )
展开式中,末3项的系数(a,χ均未知)之和为( )
- A 22
- B 12
- C 10
- D -lO
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为二项展开式的性质. 【应试指导】
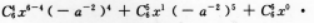
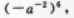
末三项系数之和为
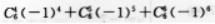
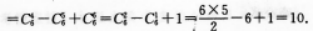
过点P(2,-3)且在两坐标轴上截距相等的直线方程是( )
- A χ+y+1=0或3χ+2y=0
- B χ-y-1=0或3χ+2y=0
- C χ+y-1=0或3χ+2y=0
- D χ-y+1=0或3χ+2y=0
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为直线的截距. 【应试指导】若直线在两坐标轴上截距相等,将直线方程转化为截距式容易判别、选项A对.选项B错,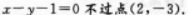 直线选项C错,
直线选项C错,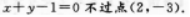 直线选项D错,直线
直线选项D错,直线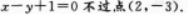
已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF⊥AB,则EF与CD所成的角的度数为( )
- A 90°
- B 45°
- C 60°
- D 30°
- 参考答案:D
- 您的答案:
参考解析:
取BC的中点G,则EG=1,FG=2,EF⊥FG,则EF与CD所成的角∠EFG=30°.
曲线|xy|+1=|x|+|y|所围成图形的面积是( )
- A 1
- B 4
- C 2
- D 16
- 参考答案:B
- 您的答案:
参考解析:
已知曲线方程可化为|x|·|y|-|x|-|y|+1=0,(|x|-1)(|y|-1)=0,所以|x|-1=0即x=±1,或|y|-1=0即y=±1.因此已知曲线表示四条平行于坐标轴的直线,即x=±1及y=±1,它们所围成的图形是边长为2的正方形,其面积为4.
直三棱柱ABC-A1B1C1中,各侧棱和底面的边长均为a,点D是CC1上任意一点,连接A1B,BD,A1D,AD,则三棱锥A-A1BD的体积为( )
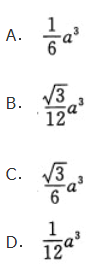
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
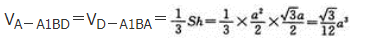
设命题甲:k=1,命题乙:直线y=kx与直线y=x+1平行,则( )
- A 甲是乙的必要条件但不是乙的充分条件
- B 甲是乙的充分条件但不是乙的必要条件
- C 甲既不是乙的充分条件也不是乙的必要条件
- D 甲是乙的充分必要条件
- 参考答案:D
- 您的答案:
参考解析:

把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为( )
- A 90°
- B 60°
- C 45°
- D 30°
- 参考答案:C
- 您的答案:
参考解析:
当三棱锥D-ABC体积最大时,平面DAC⊥平面ABC,取AC的中点O,则△DBO是等腰直角三角形,即∠DB0=45°.
有6名男生和4名女生,从中选出3名代表,要求代表中必须有女生,则不同的选法的种数是( )
- A 100
- B 60
- C 80
- D 192
- 参考答案:A
- 您的答案:
参考解析:

从6本不同的文学书和4本不同的科技书中,任意取出3本,则取到3本同类书的概率为( )
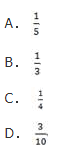
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

在正方体ABCD-A1B1C1D1中,AC所在直线与BC1所在直线所成角的大小是( )

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

已知向量a=(3,4),向量b=(0,-2),则cos(a,b)的值为( )
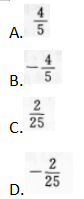
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查e-j知识点为向量的夹角. 【应试指导】求cos〈a,b〉,可直接套用公式
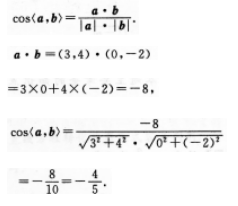
参数方程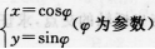 表示的图形为( )
表示的图形为( )
- A 直线
- B 圆
- C 椭圆
- D 双曲线
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为参数方程. 【应试指导】∵在cosφ、sinφ中φ为参数,消去φ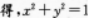
即半径为1的圆,圆心在原点.
四面体S-ABC中,各个侧面都是边长为a的正三角形,E,F分别是SC和AB的中点,则异面直线EF与SA所成的角等于( )
- A 90°
- B 60°
- C 45°
- D 30°
- 参考答案:C
- 您的答案:
参考解析:

生产一种零件,在一天生产中,次品数的概率分布列如表所示,则E(ξ)为( )

- A 0.9
- B 1
- C 0.8
- D 0.5
- 参考答案:A
- 您的答案:
参考解析:
E(ξ)=0×0.3+1×0.5+2×0.2+3×0=0.9.
已知χ轴上的一点B与点A(5,12)的距离等于13,则点B的坐标为( )
- A (10,0)
- B (0,0)
- C (10,O)或(0,0)
- D (-10,0)
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为两点间距 离公式.
【应试指导】设B(χ,0),由两点间的距离公
式得:

已知平面α、β、γ两两垂直,它们三条交线的公共点为O,过O引一条射线OP,若OP与三条交线中的两条所成的角都是60。,则OP与第三条交线所成的角为 ()
- A 30o
- B 45o
- C 60o
- D 不确定
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为异面直线间的夹角. 【应试指导】将α、β、γ看成是长方体中有公共点的三个面,OP看成是长方体的对角线,应选B.

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为利用三角函数线求角. 【应试指导】首先做出单位圆.然后根据问题的约束条件.利用三角函数线找出满足条件的α角取值范围.
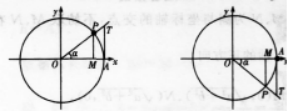
2题答案图

在棱长为2的正方体中,M、N分别为棱AA′和BB′的中点,若θ为直线CM与D′N所成的角,则sinθ=( )

- A <img src='http://tp.mxqe.com/data/876/20178175_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>
- B <img src='http://tp.mxqe.com/data/876/20178175_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>
- C <img src='http://tp.mxqe.com/data/876/20178175_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>
- D <img src='http://tp.mxqe.com/data/876/20178175_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为异面直线所成的角.
【应试指导】如图,

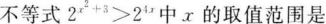
- A x<1
- B x>3
- C x<1或x>3
- D x≤1或x≥3
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为指数函数的性质.
【应试指导】求x的取值范围,即求函数的定义域.

命题甲:x^2=y^2,命题乙:x=y(x,y∈R),甲是乙的( )
- A 充分但非必要条件
- B 必要但非充分条件
- C 充要条件
- D 即非充分又非必要条件
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为简易逻辑.
【应试指导】
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为反比例函数的图像 【应试指导】本题属于读图题型,在寻求答案时,要着重讨论方程的表达式.
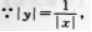
∴(1)当χ>0时,
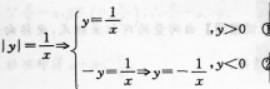
∴(2)当χ<0时,
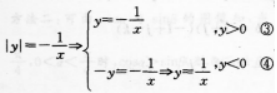
如图,
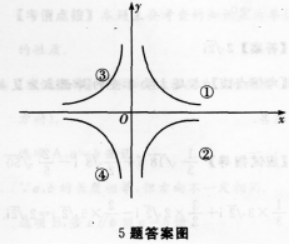

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为函数的解析式. 【应试指导】
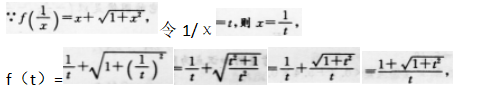
函数与用哪个英文字母无关,只与对应法则、定义域有关.

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为三角函数的最值. 【应试指导】
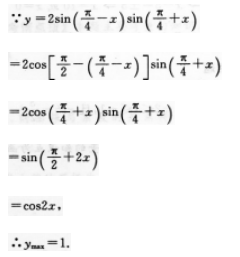
注:求三角函数的最值时.应先将函数转化为sinχ或cosχ的函数,再讨论函数的取值情况.
已知集合M={2,3.5,a),N={1,3,4,b},若M∩N={1.2,3),则a,b的值为( )
- A a=2,b=1
- B a=1,b=1
- C a=1,b=2
- D a=1.b=5
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为集合的运算.
【应试指导】M∩N={2,3.5,a}∩{1,3,4,6}={1,2,3},又∵M中无“1”元素.而有“a”元素.只有“a=1,而N中无”2”元素,而有“b”元素,只有b=2.
已知α、β为锐角,cosα>sinβ,则( )

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为三角函数的图像及诱导公式.
【应试指导】方法一:由cosα>sinβ,诱导公式
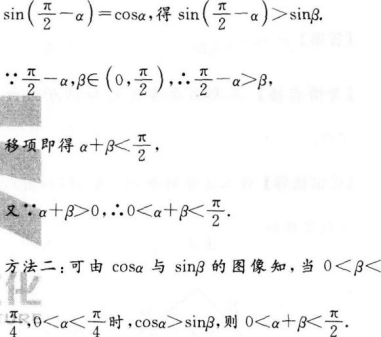


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
余弦定理是解斜三角形的重要公式,本题利用余弦定理及三角形面积公式
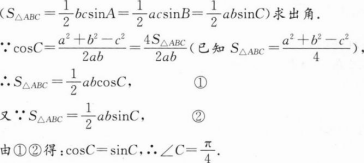
如果不共线的向量a和b有相等的长度,则(a+b)(a-b)=( )
- A 0
- B 1
- C -1
- D 2
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为向量的运算。
【应试指导】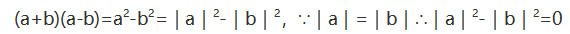
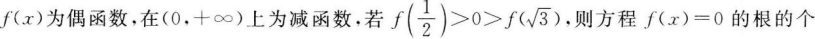 数是( )
数是( )
- A 2
- B 2或1
- C 3
- D 2或3
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为偶函数的性质.
【应试指导】由已知f(x)为偶函数,∴f(x)关于y轴对称,

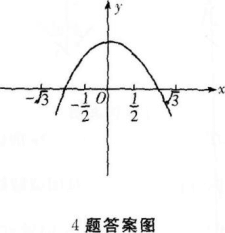

- A a=3,b=5,C=2
- B a=3,b=-2,C=5
- C a=-3,b=-5,C=2
- D a=2,b=5,C=-3
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为函数的反函数.
【应试指导】
- A <img src='http://tp.mxqe.com/data/876/20178170_0.png' alt='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷' title='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷'>
- B <img src='http://tp.mxqe.com/data/876/20178170_0.png' alt='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷' title='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷'>
- C <img src='http://tp.mxqe.com/data/876/20178170_0.png' alt='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷' title='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷'>
- D <img src='http://tp.mxqe.com/data/876/20178170_0.png' alt='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷' title='理科数学,押题密卷,2022年成人高等考试《理科数学》(高升本)押题密卷'>
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为圆心角.
【应试指导】如图,要求圆心角,先找出直线与圆的交点,两个交点之间的劣弧所对的圆心角即为所求.

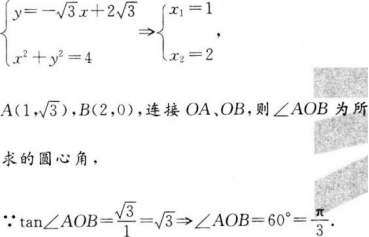
过点(2,-2)且与双曲线x^2-2^y2=2有公共渐近线的双曲线方程是( )
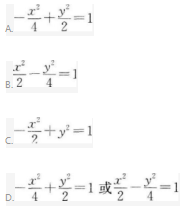
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为双曲线的渐近线.
【应试指导】将双曲线方程化为标准式方程.如图
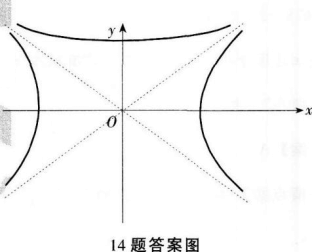


注:本题是用待定系数法来解的.

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为弧度制的面积公式. 【应试指导】利用弧度制中的面积公式S=1/2L·r.如图,
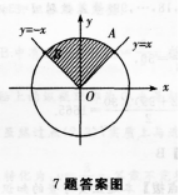
∵χ2+y2=4-22,
∴r=2.
AB=L=1/4·2πr

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
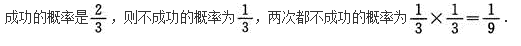
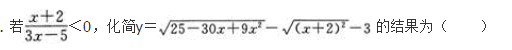
- A y=-4x
- B y=2-x
- C y=3x-4
- D y=5-x
- 参考答案:A
- 您的答案:
参考解析:
- A 55
- B 70
- C 85
- D 100
- 参考答案:C
- 您的答案:
参考解析:
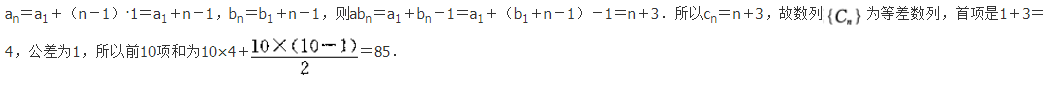

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
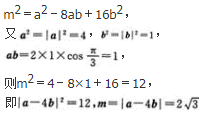

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

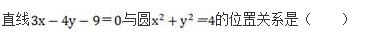
- A 相交但直线不过圆心
- B 相交但直线通过圆心
- C 相切
- D 相离
- 参考答案:D
- 您的答案:
参考解析:
设Z∈C(C为复数集).且满足条件|Z-2|+|Z+2|=10,那么复数Z对应的点的集合表示的图形为( )
- A 圆
- B 椭圆
- C 抛物线
- D 双曲线
- 参考答案:B
- 您的答案:
参考解析:
【考情点拨】本题主要考查的知识点为椭圆的定义.
【应试指导】如图,
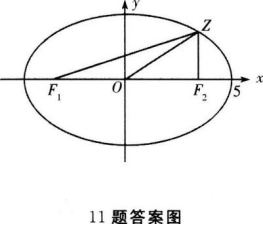


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
- A 最大值4,最小值0
- B 最大值0,最小值-4
- C 最大值4,最小值-4
- D 最大值、最小值都不存在
- 参考答案:C
- 您的答案:
参考解析:
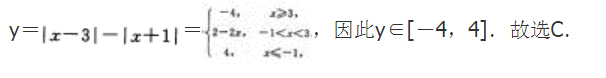
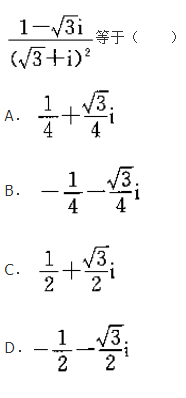
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
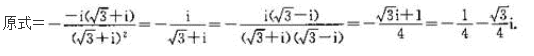
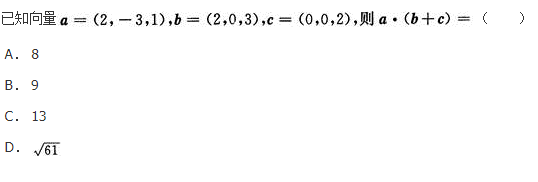
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
原式=2×2(-3)×0+1×5=9
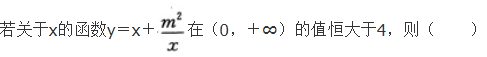
- A m>2
- B m<-2或m>2
- C -2<m<2
- D m<-2
- 参考答案:B
- 您的答案:
参考解析:
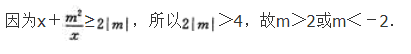

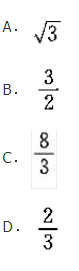
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:


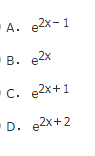
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
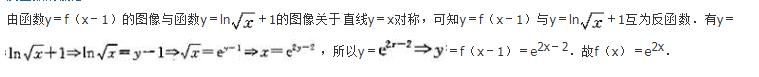

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

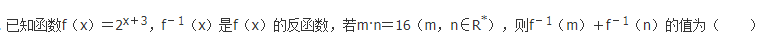
- A ﹣2
- B 1
- C 4
- D 10
- 参考答案:A
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
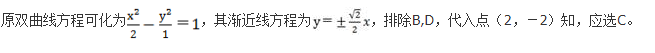

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
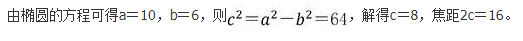
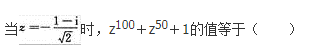
- A 1
- B -1
- C i
- D -i
- 参考答案:D
- 您的答案:
参考解析:
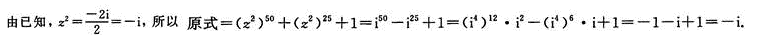

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
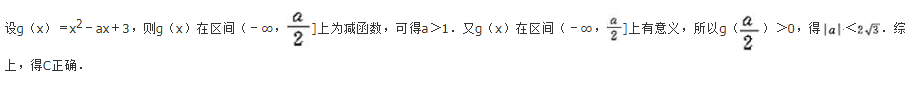

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
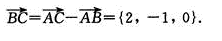

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

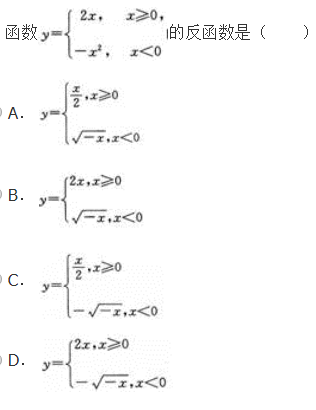
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:


- A 10,6
- B 10,8
- C 8,6
- D 以上都不对
- 参考答案:A
- 您的答案:
参考解析:
分段函数的最大值为各段上最大值中的最大者,最小值为各段上最小值中的最小者.
当1≤x≤2时,8≤2x+6≤10;
当-1≤x<1时,6≤x+7<8.
所以f(x)min=f(-1)=6,f(x)max=f(2)=10.故选A.

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
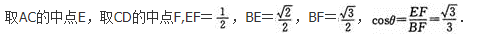
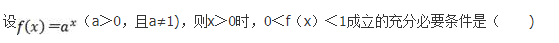
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
有函数定义可知,应选B。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
从点M(x,3)向圆(x4-2)2+(y+2)2=1作切线,切线长的最小值等于
- A 4
- B <img src='http://tp.mxqe.com/data/876/20178153_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>?
- C 5
- D √26
- 参考答案:B
- 您的答案:
参考解析:

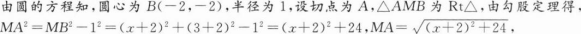
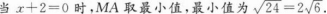
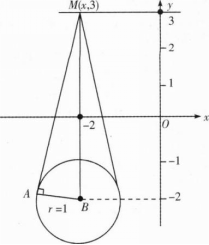
已知函数f(x)=ax2+b的图像经过点(1,2),且其反函数f-1(x)的图像经过点(3,0),则函数f(x)的解析式是( )
- A <img src='http://tp.mxqe.com/data/876/20178154_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>?
- B f(x)=-x2+3
- C f(x)=3x2+2
- D f(x)=x2+3
- 参考答案:B
- 您的答案:
参考解析:
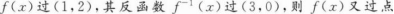
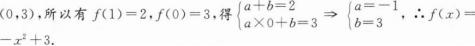
若a
- A <img src='http://tp.mxqe.com/data/876/20178164_0.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>?
- B <img src='http://tp.mxqe.com/data/876/20178164_0_1.png' alt='理科数学,章节练习,理科数学押题' title='理科数学,章节练习,理科数学押题'>?
- C |a|>|b|
- D a2>b2
- 参考答案:B
- 您的答案:
参考解析:

若三角形三边之比为2:3:4,则此三角形的最小角为弧度.
已知正圆锥的底面半径是1Cm,母线为3Cm,P为底面圆周上一点,由P绕过圆锥回到P点的最短路径如图所示,由顶点V到这条路线的最小距离是多少?
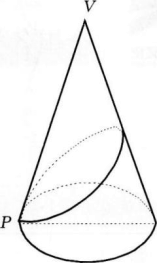
- 参考答案:
- 您的答案:
参考解析:
圆锥的曲面沿着母线剪开,展开成一个平面(如下图).
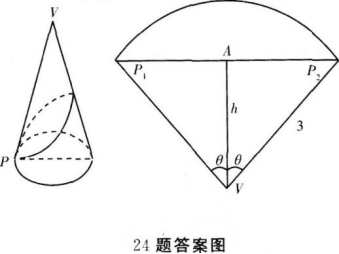
其半径VP=3,弧长=2π·1=2π的扇形.
∵圆锥的底面半径为1,于是嗣绕圆锥的最短路线对应于扇形内是P1到P2的最短距离,就是弦P1P2,由V到这条路线的最短距离是图中的线段h=AV.依据弧长公式2π=20·3,
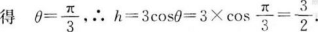
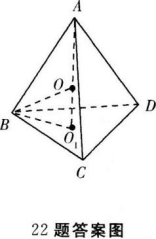
正四面体ABCD内接于半径为R的球,求正四面体的棱长.
- 参考答案:
- 您的答案:
参考解析:
在正四面体(如图)中作AO1⊥底面BCD于O1.
∴O1为△BCD的中心,
∵OA-OB-OC-OD=R,
∴球心在底面的BCD的射影也是O1,
∴A、O、O1三点共线,
设正四面体的棱长为x.
甲、乙二人各射击一次,若甲击中目标的概率为0.8,乙击中目标的概率为0.6.试计算:(Ⅰ)二人都击中目标的概率;
(Ⅱ)恰有一人击中目标的概率;
(Ⅲ)最多有一人击中目标的概率.
函数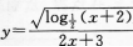 的定义域是__________
的定义域是__________
圆心在Y轴上,且与直线χ+y-3=0及χ-y-1=0都相切的圆的方程为_____.
已知A(2,1),B(3,-9),直线z:5χ+y-7=0与直线AB交于P点,点P分AB所成的比为__________.
过点(2,1)且与直线y=x+1垂直的直线的方程为______.
直线3x+4y-12=0与x轴、y轴分别交于A,B两点,O为坐标原点,则△OAB的周长为_________
长方体有一个公共顶点的三条棱的比为2∶3∶5,全面积是1550,则此长方体的体积为_____.
- 参考答案:
- 您的答案:
参考解析:
依题意可设长方体的三条同顶点棱分别为2x,3x,5x,于是有
2(2x·3x+2x·5x+3x·5x)=1550,
62x2=1550,x2=25,x=5或x=-5(不合题意,舍去),
所以长方体三度分别为10,15,25,因此长方体的体积为3750.
为了检查一批零件的长度,从中抽取10件,量得它们的长度如下(单位:mm):22.36、22.35、22.33、22.35、22.37、22.34、22.38、22.36、22.32、22.35则样本的平均数(结果保留到小数点第二位)为____________,这组数据的方差为__________.
一口袋内装一些大小相同的红球、白球和黑球,从中摸出1个球,摸出红球的概率为0.42,摸出白球的概率为0.28,则摸出红球或白球的概率为_______.
某射手射击一次,击中目标的概率为0.9,他连续射击4次且各次射击是否击中相互之间没有影响,那么他第2次未击中,其他3次都击中的概率是___________
.
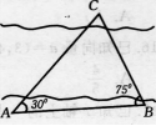
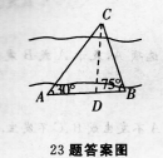
为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得∠CAB=30o,∠CBA=75o,AB=120m,求河的宽.
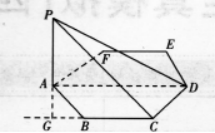
已知正六边形ABCDEF的边长为a,PA为过点A而垂直于正六边形所在平面M的垂线,且PA=a,求:
(I)点P到AB、BC、CD各边的距离;
(II)PD与平面M所成的角.
- 参考答案:
- 您的答案:
参考解析:
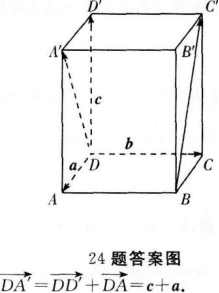
(I)如图所示,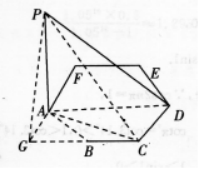
24题答案图
∵PA上平面M,∴PA上BC,
∴点P到AB的距离为a.过A作BC的垂线交CB的延长线于G,连结PG,
∴BC上平面APG,即PG⊥AB,
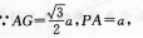
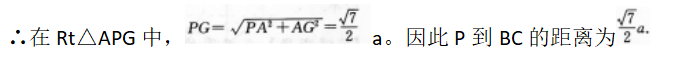
∵PA上平面M,
∴AC是PC在平面M上的射影,
又∵AD是正六边形ABCDEF外接圆的直径,
∴∠ACD=90o.
因此AC⊥CD,所以CD⊥平面ACP,即PC是P到CD的距离,
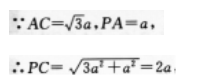
因此P到CD的距离为2a.
(Ⅱ)设PD与DA所夹的角为口,在Rt△PAD中,
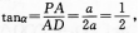
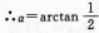 (VI)为PD与平面M所夹的角.
(VI)为PD与平面M所夹的角.
把边长是a的正方形铁皮的四角切去相等的正方形,再将它折起,做成一个无盖且底面为正方形,高为切去的正方形边长的箱子,箱底边多长时,箱子的容积最大?
某城有东西方向的街道七条,相邻两街的距离为b;南北方向的街道八条,相邻两街的距离为12,形成一个矩形.
(I)从A到D的最短途径有多少条
(U)从A经B和C到D的最短途径有多少条
从椭圆上χ2+2y2=2的右焦点引一条倾斜45o的直线,以这条直线与椭圆的两个交点P、Q及椭圆中心。为顶点,组成△OPQ.
(I)求AOPQ的周长;
(Ⅱ)求AOPQ的面积.
设离散型随机变量ξ的分布列如下表所示,那么ξ的期望等于?.

已知i,j,k为单位向量且互相垂直,向量a=i+j,b=-i+j-k,则a·b?.

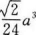

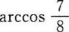
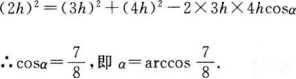


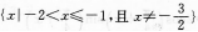 【考情点拨】本题主要考查的知识点为函数的定义域.
【考情点拨】本题主要考查的知识点为函数的定义域.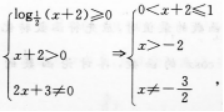
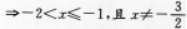
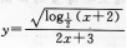 的定义域是
的定义域是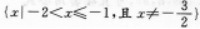
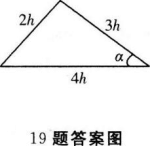
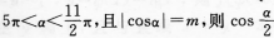 的值等于__________
的值等于__________
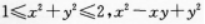 的值域为__________
的值域为__________
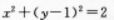
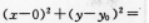 r2(如图)
r2(如图)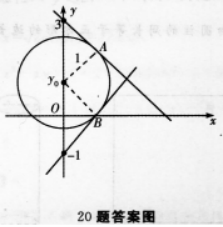


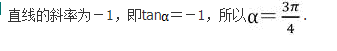
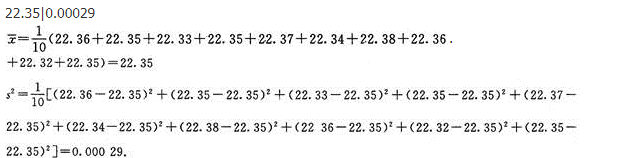
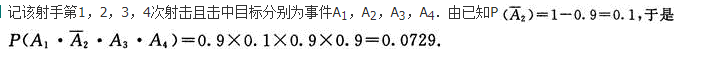

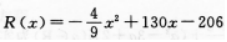 (百元),成本函数为
(百元),成本函数为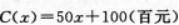 ,当每月生产多少台时,获利润最大最大利润为多少
,当每月生产多少台时,获利润最大最大利润为多少
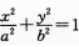 和圆
和圆 ,M、N为圆与坐标轴的交点,求证:圆的弦MN是椭圆的切线.
,M、N为圆与坐标轴的交点,求证:圆的弦MN是椭圆的切线.

 1716条. (Ⅱ)同理,从A到B再到C,最后到D的最短途径共
1716条. (Ⅱ)同理,从A到B再到C,最后到D的最短途径共