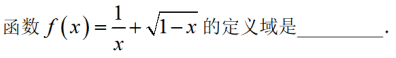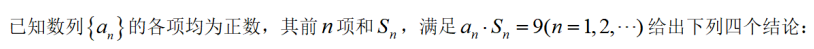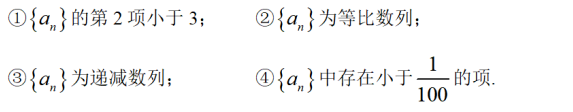若复数z满足i.z=3-4i，则|z|=
- A 1
- B 5
- C 7
- D 25
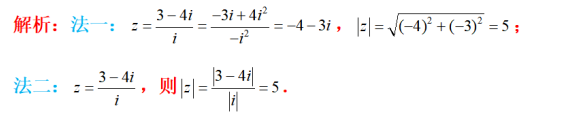
若直线2x+y-1=0是圆(x-a)2 +y2=1的一条对称轴，则a=
- A 1/2
- B -1/2
- C 1
- D -1
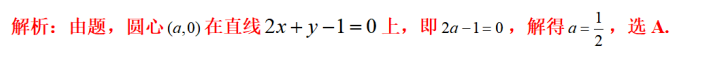
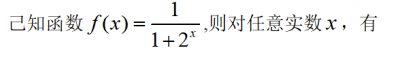
- A f(-x)+f(x)=0
- B f(-x)-f(x)=0
- C f(-x)+f(x)=1
- D f(-x)-f(x)=1/3
已知函数f（x）=cos2x-sin2x，则
- A A
- B B
- C C
- D D
设{an}是公差不为0的无穷等差数列，则“{an}为递增数列”是“存在正整数N0，当n＞N0时，an＞0”的
- A 充分而不必要条件
- B 必要而不充分条件
- C 充分必要条件
- D 既不充分也不必要条件
在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献，如图描述了一定条件下二氧化碳所处的状态与T和1gP的关系，其中T表示温度，单位是K；P表示压强，单位是bar，下 列结论中正确的是
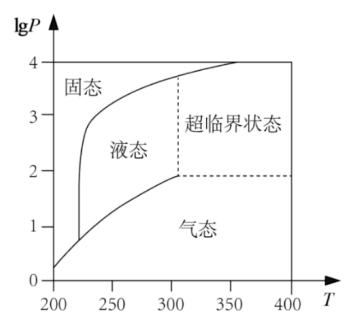
- A 当T=220，P=1026时，二氧化碳处于液态
- B 当T=270，P=128时， 二氧化碳处于气态
- C 当T=300，P=9987时，二氧化碳处于超临界状态
- D 当T=360，P= 729时，二氧化碳处于超临界状态
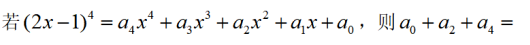
- A 40
- B 41
- C -40
- D -41
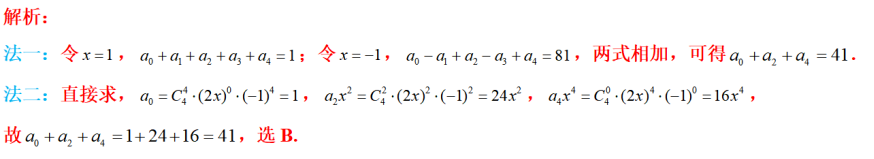
已知正三棱锥P- ABC的六条棱长均为6，S是△ABC及其内部的点构成的集合，设集合:T={Q∈S|PQ≤5}，则T表示的区域的面积为
- A 3π
- B π
- C 2π
- D 3π
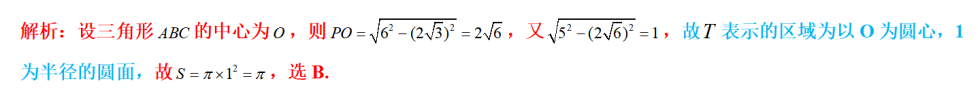
在△ABC中，AC=3，BC=4，∠C=90°，P为△ABC所在平面内的动点，且PC=1，则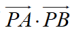
的取值范围是
- A [-5,3]
- B [-3,5]
- C [-6,4]
- D [-4,6]
在△ABC中，sin2C= √3 sinC.
(I)求∠C:
(II)若b=6，且△ABC的面积为6√3，求△ABC的周长.
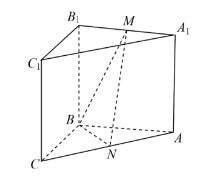
如图，在三棱柱ABC-A1B1C1中，侧面BCC1B1为正方形，平面BCC1B1⊥平面ABB1A1，AB=BC=2，M，N分别为A1B1，AC的中点
（1）求证：MN∥BCC1B1
（2）(I)再从条件①、条件②这两个条件中选择-一个作为已知，求直线AB与平面BMN所成角的正弦值。
条件①:AB⊥MN;
条件②: BM = MN.
注:如果选择条件①和条件②分别解答，按第一个解答计分。
在校运动会.上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9.50m以上(含9.50m)的同学将获得优秀奖，为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：
甲: 9.80, 9.70, 9.55, 9.54, 9.48, 9.42, 9.40, 9.35, 9.30, 9.25;
乙: 9.78, 9.56, 9.51, 9.36, 9.32, 9.23;
丙: 9.85, 9.65, 9.20, 9.16.
假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立
(I)估计甲在校运动会铅球比赛中获得优秀奖的概率;
(II) 设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计X的数学期望EX ;
(II)在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大? (结论不要求证明)
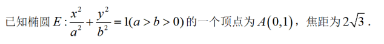
(I) 求椭圆E的方程:
(Ⅱ)过点P(-2,1)作斜率为h的直线与椭圆E交于不同的两点B,C，直线4B,.4C分别与x轴交于点M,N，当|MN|=2时，求k的值.
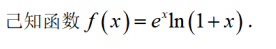
(I) 求曲线y= f(x)在点(0,f(0))处的切线方程;
(II)设g(x)= f"(x)，讨论函数g(x)在[0,+∞).上的单调性;
(II)证明:对任意的s,t∈(0,+∞)，有f(s+t)> f(s)+ f(t).
