设f(x)与g(x)是定义在同一区间增函数,下列结论一定正确的是( )。
- A f(x)+g(x)是增函数
- B f(x)- g(x)是减函数
- C f(x)g(x)是增函数
- D f(g(x))是减函数
- 参考答案:A
- 您的答案:
参考解析:
根据函数的增减性,增+增=增,可知f(x)+g(x)是增函数。故本题选A。
甲、乙两位同学分别前往不同公司的面试,甲同学被选中的概率是1/7,乙同学被选中的概率是1/5,则两位同学中至少有一位被选中的概率是( )。
- A 1/7
- B 2/7
- C 11/35
- D 12/35
- 参考答案:C
- 您的答案:
参考解析:
两位同学中至少有1位被选中的反面是两位同学都没有被选中,显然对立事件的概率更容易计算,两位同学都没有被选中的概率是:
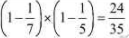
极限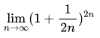 的值是( )。
的值是( )。
- A 0
- B 1
- C e
- D ∞
- 参考答案:C
- 您的答案:
参考解析:
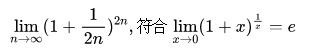
已知向量a与b的夹角为π/3,且|a|=1,|b|=2,若m=λa+b与n=2a- b互相垂直,则λ的为( )。
- A -2
- B -1
- C 1
- D 2
- 参考答案:D
- 您的答案:
参考解析:
因为m,n垂直,所以mn=0,即(λa+bn)(2a-b)=0,2λ|a|2+(2-λ)|a||b|cosπ/3-|b|2=0,得出λ=2
设A和B为n阶方阵子一定正确的是( )。
- A A+B=B+A
- B AB=BA
- C <img src='http://tp.mxqe.com/data/438/19070791_0.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力高中真题' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力高中真题'>
- D <img src='http://tp.mxqe.com/data/438/19070791_0_1.png' alt='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力高中真题' title='中学数学学科知识与教学能力,章节练习,中学数学学科知识与教学能力高中真题'>
- 参考答案:A
- 您的答案:
参考解析:
由于已知A与B均为n阶方阵,则可知A+ B= B+ A,故本题选A。
若向量a=(1,0,1), a2=(0,1,1), a3=(2, λ,2)线性相关, 则 λ的值为( )。
- A -1
- B 0
- C 1
- D 2
- 参考答案:B
- 您的答案:
参考解析:
向量组线性相关的充要条件是它们构成的行列式值等于0,所以 =0,解得λ=0
=0,解得λ=0
下列数学成就是中国著名成就的是( )。
①勾股定理②对数③割圆术 ④更相减损术
- A ①②③
- B ①②④
- C ①③④
- D ②③④
- 参考答案:C
- 您的答案:
参考解析:
①、③、④都属于中国古代的数学成就,而②中提到的对数是英国科学家约翰纳皮尔发明的。故本题选C。
下列语句是命题的是( )。
①2x<1
②x-3是整数
③存在一个x∈z,使2x-1=5
④对任意一个无理数x,x+2也是无理数
- A ①②
- B ①③
- C ②③
- D ③④
- 参考答案:D
- 您的答案:
参考解析:
由命题的概念:可以判断真假的陈述句叫做命题。对于①,不是陈述句,故不是命题;对于②,由于不知道x的具体范围,无法判断其真假,故不是命题;对于③、④,即为可以判断真假的陈述句,是命题。故本题选D。
已知函数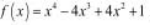 ,求函数f(x) 的单调区间和极值。
,求函数f(x) 的单调区间和极值。
已知某班级80%的女生和90%的男生选修滑冰,且该班中60%的学生是女生。
(1)从该班随机选取一 名学生,求这名学生选修滑冰的概率;(3分)
(2)在该班选修滑冰的学生中随机选取一名学生, 求这名学生是女生的概率。(4 分)
简述研究椭圆几何性质的两种方法。
- 参考答案:
- 您的答案:
参考解析:
研究椭圆几何性质的两种方法:
①用曲线方程研究几何性质,例如通过椭圆方程研究x、y的取值范围,通径,焦半径取值范围等,能够解释椭圆标准方程a,b,c的几何意义,这种方法是数形结合的数学思想方法的典范。
②用代数方法研究几何性质,在研究过程中,经历从图形直观抽象几何性质的过程,提取出利用代数方法研究几何性质的一般方法,建立离心率模型。
简述在教材平面教学设计内容中设置下列习题的设计意图(答出两条即可)。已知0<x<1,0<y<1,求证不等式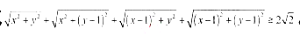
并说明其设计意义。
- 参考答案:
- 您的答案:
参考解析:
设计意图:?
(1)不等式左侧分别是(x,y)到(0,0) ,(0,1), (1,0), (1,1)的距离,可以提升学生对两点间距离公式的理解和应用;?
(2)(x,y) 到这四个点的距离之和,可以结合这四个点在平面上的位置进行分析,xy的范围对应第一象限边长为1的正方形范围,在这道题的解决过程中,增强了学生数形结合的能力。
已知抛物线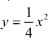 。
。
(1)求抛物线在点(2,1)处的切线方程(5 分)
(2)如图,抛物线在点P(xo, yo)(xo?≠0)处的切线PT与y轴交于点M,光源在抛物线焦点F(0,1)处,入射光线FP经抛物线反射后的光线为PQ,即∠FPM =∠QPT,求证: 直线PQ与y轴平行。(5分)

论述数学史在数学教学各阶段(导入、形成、应用)的作用。
- 参考答案:
- 您的答案:
参考解析:
在导入部分,可以通过介绍历史上的数学家,例如欧几里得在《几何原本》中将圆的切线定义为“ 与圆相遇但延长后不与圆相交的直线”。
形成部分:并让学生回忆圆的切线定义,引导学生对切线定义进行改进,并借助《几何原本》中的有关命题,引导学生得出新的切线定义。
应用部分:从形到数,引导学生得出导数的定义。
下面是甲、乙两位教师的教学片段。
[教师甲]
教师甲:在平面直角坐标系中,点(x, y)关于y轴的对称点是什么?
学生1: (-x, y)。
教师甲:为了研究函数的对称性,请大家填写下表,观察给定函数的自变量x互为相相反数时,对应的函数值之间具有什么关系?

学生2:通过计算发现,自变量互为相反数时,对应的函数值相等,可以用解析表示,

教师甲:通常我们把具有以上特征的函数称为偶函数,请大家试着给出偶函数的定义。
[教师乙]
教师乙:我们已经研究了函数的单调性,并且用符号语言精确地描述了函数的单调性,今天我们研究函数的其他性质,请大家画出函数f(x)=x2和g(x)= |x|的图象,并观察它们的共同特征。
(通过观察,学生发现这函数的图象都关于y轴对称)
教师乙:类比函数的单调性,你能用符号语言精确地描述“数图象关于y轴对称”这概念吗?
(通过观察,学生发现f(-x)=f(x).)
教师乙:通常我们把函数上述特征的函数称为偶函数,请大家试着给出偶函数的定义。
问题:
(1)写出偶函数的定义,并简要说明函数奇偶性的作用; (1分)
(2)对甲、乙两位教师的教学进行评价。(10分)
- 参考答案:
- 您的答案:
参考解析:
(1)偶函数的定义:设函数f(x)的定义域为D,如果Vx∈D,都有-x∈D,且f(-x)=f(x), 那么函数f(x)就叫做偶函数。研究奇偶性作用:函数的奇偶性跟其图象的对称性紧密相关,奇函数关于原点对称,偶函数关于y轴对称;有奇偶性的函数只需知道y轴一侧的性质就可推出y轴另一侧的性质,在对函数性质的分析上可以简化运算和分析。
(2)甲教师在对偶函数的新授过程中,着重引导学生通过计算结果分析得到偶函数的定义,缺乏学生主动探索的过程,直接给出本节课的研究主题是对称性,太过于直截了当;而乙教师在教学过程中,引导学生进行了图象观察和结论的探索,更加符合新课改学生是学习主体的理念,并且结合了之前学过的单调性进行导入,在下定义的时候引导学生结合之前学过的知识进行尝试,使学生在学习新知识的同时对旧知识得到很好的巩固。
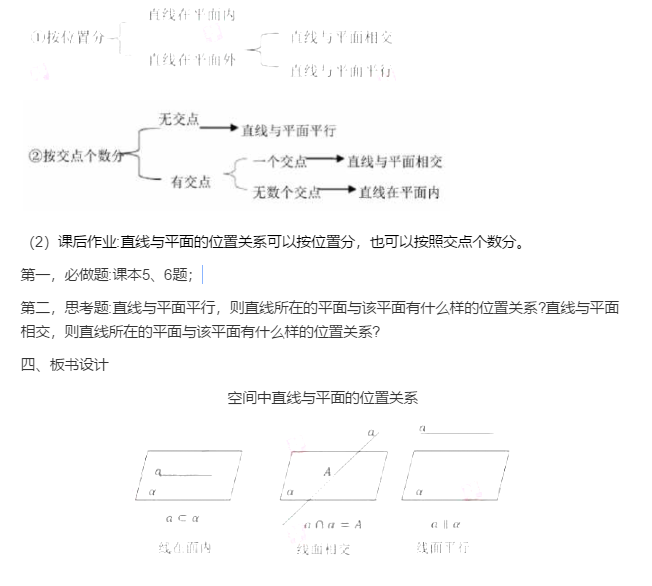
下面是高一下学期教材“空间中直线与平面的位置关系”的部分内容。

根据上面的内容,完成下列任务:
(1)画出直线与平面的位置关系的示意图,并举出生活中体现这三种位置关系的实例; (12 分)
(2)写出这部分内容的教学设计,包括教学目标、教学重点、教学过程(含引导学生探究的活动和设计意图)。(18 分)

 且平行于于直线
且平行于于直线 的平面方程。
的平面方程。