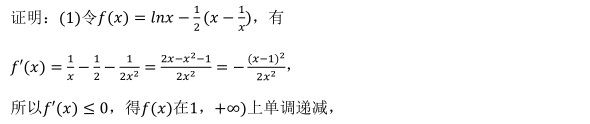单选题
1/0
1.
已知集合A = [2,4), B = [3,5], 则(∁ R A) ∩ B = ( )
- A (4,5]
- B [4,5]
- C (−∞, 2) ∪ [3, +∞)
- D (−∞, 2] ∪ [3, +∞)
未回答
- 参考答案:B
- 您的答案:
参考解析:
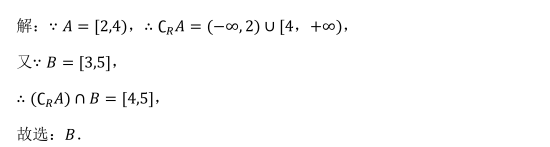
单选题
2/0
2.

- A 2
- B 3
- C 2√3
- D 3√2
未回答
- 参考答案:D
- 您的答案:
参考解析:
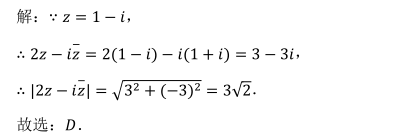
单选题
3/0
3.
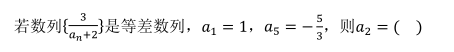
- A -1
- B 1
- C -2
- D 2
未回答
- 参考答案:A
- 您的答案:
参考解析:

单选题
4/0
4.

- A A
- B B
- C C
- D D
未回答
- 参考答案:D
- 您的答案:
参考解析:

单选题
5/0
5.
已知某函数的图象如图所示, 则该函数的解析式可能为( )
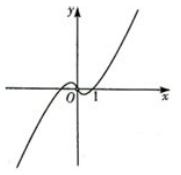
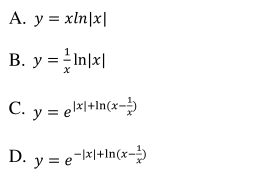
- A A
- B B
- C C
- D D
未回答
- 参考答案:A
- 您的答案:
参考解析:
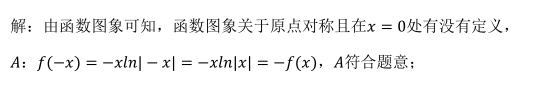

单选题
6/0
6.

- A A
- B B
- C C
- D D
未回答
- 参考答案:A
- 您的答案:
参考解析:

单选题
7/0
7.
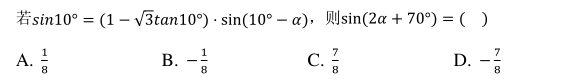
- A A
- B B
- C C
- D D
未回答
- 参考答案:C
- 您的答案:
参考解析:
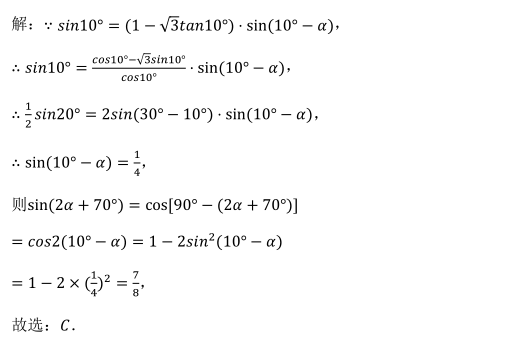
单选题
8/0
8.


- A A
- B B
- C C
- D D
未回答
- 参考答案:D
- 您的答案:
参考解析:
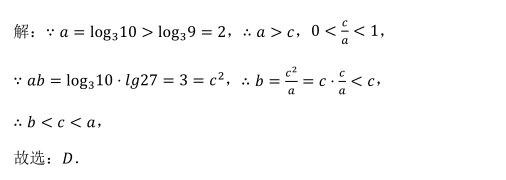
单选题
9/0
9.
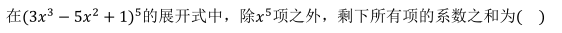
- A 299
- B -301
- C 300
- D -302
未回答
- 参考答案:A
- 您的答案:
参考解析:

单选题
10/0
10.
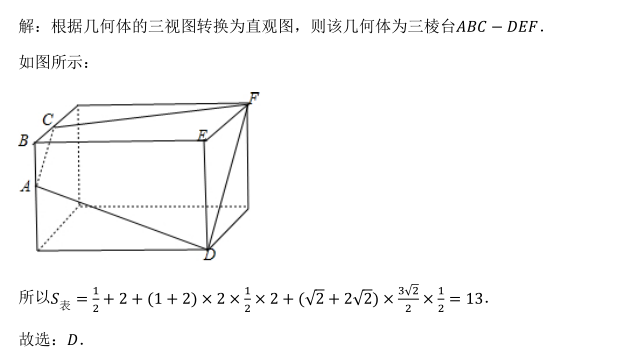
如图, 网格纸上小正方形的边长为1, 粗实线画出的是某三棱台的三视图, 则该几何体的表面积为( )
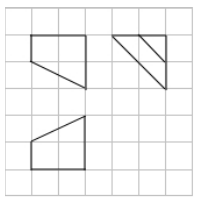
- A 8
- B 11
- C 12
- D 13
未回答
- 参考答案:D
- 您的答案:
参考解析:
单选题
11/0
11.
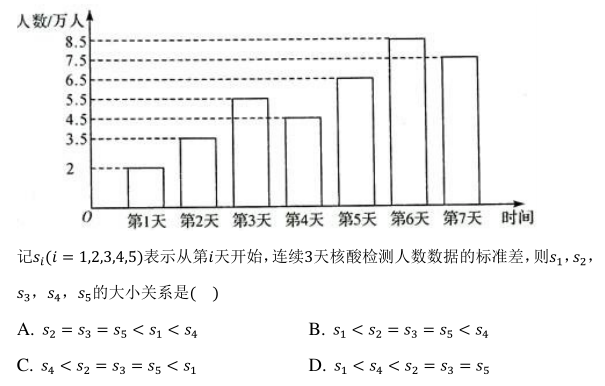
为了防控疫情, 某市进行核酸检测, 经统计, 该市在某一周内核酸检测的人数(单位: 万人)如图所示:
- A A
- B B
- C C
- D D
未回答
- 参考答案:A
- 您的答案:
参考解析:

单选题
12/0
12.
- A A
- B B
- C C
- D D
未回答
- 参考答案:C
- 您的答案:
参考解析:
填空题
13/0
13.
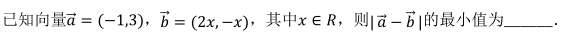
未回答
- 参考答案:√5
- 您的答案:
参考解析:
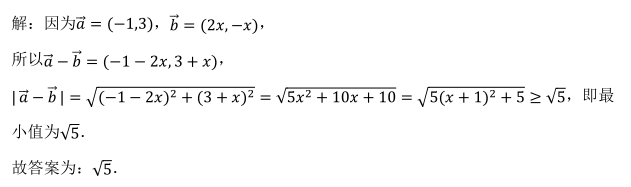
填空题
14/0
14.
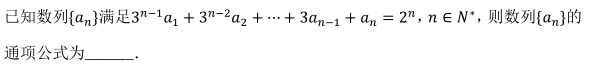
未回答
- 参考答案:
- 您的答案:
参考解析:
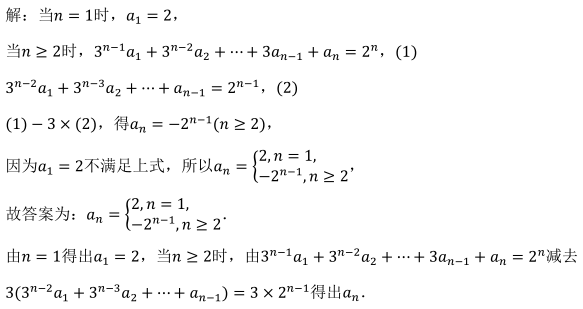
填空题
15/0
15.

未回答
- 参考答案:60°
- 您的答案:
参考解析:

填空题
16/0
16.
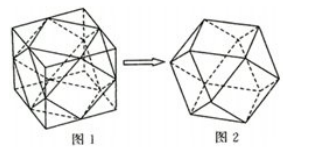
阿基米德多面体(Archimedean polyhedra)是由两种或三种正多边形面组成的半正多面体.它共有13种,其特点是棱长相等.如图1,顺次连接棱长为2的正方体各棱的中点,得到一个阿基米德多面体,如图2,在此阿基米德多面体的所有棱中任取两条,则两条棱垂直的概率为_
未回答
- 参考答案:4/23
- 您的答案:
参考解析:

问答题
17/0
17.
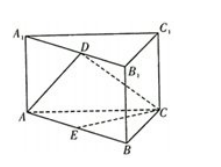
已知三棱柱ABC-A1B1C1中,∠ACB=90°,BB1=2BC,AA1⊥平面ABC,AC=BC,E为AB的中点,D为A1B1上一点
(1)求证:AD⊥CE
(2)当D为A1B1的中点时,求二面角C-AD-B1的余弦值
未回答
- 参考答案:

- 您的答案:
参考解析:
暂无解析
问答题
18/0
18.
在△ABC中,角A,B,C的对边分变为a,b,c,且√2a+c=2b
(1)求cosB的最小值
(2)若2asinA=(2b-c)sinB+(2c-b)sinC,求角C
未回答
- 参考答案:

- 您的答案:
参考解析:
暂无解析
问答题
19/0
19.
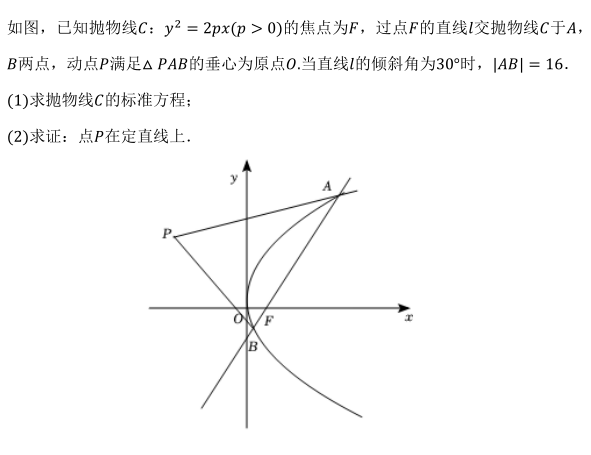
未回答
- 参考答案:

- 您的答案:
参考解析:
暂无解析