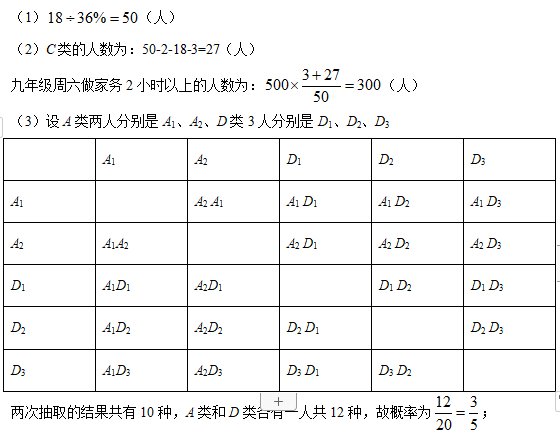
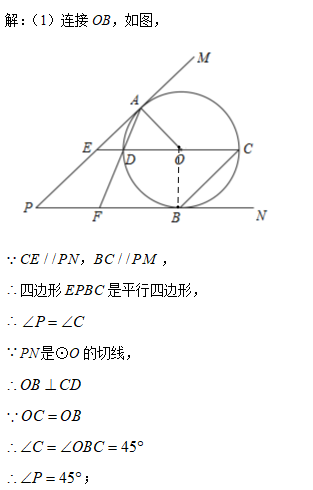
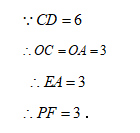﹣2022的相反数是( )
- A ﹣2022
- B 2022
- C ±2022
- D 2021
- 参考答案:B
- 您的答案:
参考解析:
【分析】根据相反数的定义:相反数是符号不同,数字相同的两个数;改变-2022前面的符号,即可得-2022的相反数,再与每个选项比较得出答案.
【详解】解:由相反数的定义得,-2022的相反数是2022,
故选B.
【点睛】本题考查了相反数的定义,一个数的相反数就是在这个数前面添上“-”号.
如图,与∠1是内错角的是( )

- A ∠2
- B ∠3
- C ∠4
- D ∠5
- 参考答案:C
- 您的答案:
参考解析:
【分析】根据内错角的定义,即两条直线被第三条直线所截,位于截线的两侧,且夹在两条被截直线之间的两个角,解答即可.
【详解】根据内错角的定义,得:∠1是内错角的是∠4.
故选:C
【点睛】本题主要考查了内错角
![]()
定义,解题的关键是熟练掌握并理解内错角的定义.
骰子各面上的点数分别是1,2,…,6,抛掷一枚骰子,点数是偶数的概率是( )
-
A
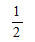
-
B
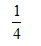
-
C

- D 1
- 参考答案:A
- 您的答案:
参考解析:
已知∠α=25°30′,则它的余角为( )
- A 25°30′
- B 64°30′
- C 74°30′
- D 154°30′
- 参考答案:B
- 您的答案:
参考解析:
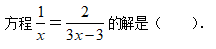
- A x=﹣2
- B x=﹣1
- C x=1
- D x=3
- 参考答案:D
- 您的答案:
参考解析:
一组数据4,6,x,7,10的众数是7,则这组数据的平均数是( )
- A 5
- B 6.4
- C 6.8
- D 7
- 参考答案:C
- 您的答案:
参考解析:
【分析】先根据众数的定义求出x的值,再根据平均数的计算公式列式计算即可.
【详解】解:∵数据4、6、x、7、10的众数是7,
∴x=7,
∴这组数据的平均数是(4+6+7+7+10)÷5=6.8;
故答案为:C.
【点睛】此题考查了众数和平均数,根据众数的定义求出x的值是本题的关键,众数是一组数据中出现次数最多的数.
下列各式计算正确的是( )
-
A
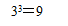
-
B

-
C
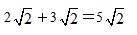
-
D
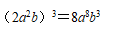
- 参考答案:C
- 您的答案:
参考解析:
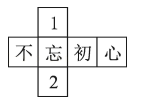
下列展开图中,不是正方体展开图的是( )
-
A
-
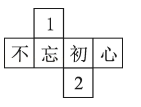
B
-
C

-
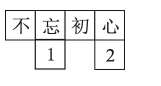
D
- 参考答案:D
- 您的答案:
参考解析:
【分析】根据正方体的展开图特征解题.
【详解】解:A.是正方体的展开图,故A不符合题意;
B.是正方体的展开图,故B不符合题意;
C.是正方体的展开图,故C不符合题意;
D.不是正方体的展开图,故D符合题意,
故选:D.
【点睛】本题考查正方体的展开图,熟知正方体的11种展开图是解题关键.
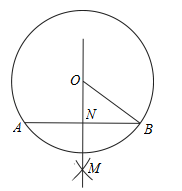
如图,在⊙O中,尺规作图的部分作法如下:(1)分别以弦AB的端点A、B为圆心,适当等长为半径画弧,使两弧相交于点M;(2)作直线OM交AB于点N.若OB=10,AB=16,则tan∠B等于( )
-
A
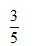
-
B
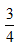
-
C
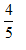
-
D
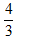
- 参考答案:B
- 您的答案:
参考解析:
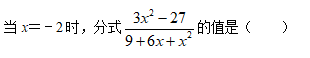
- A ﹣15
- B ﹣3
- C 3
- D 15
- 参考答案:A
- 您的答案:
参考解析:
下列四个命题:①直径是圆的对称轴;②若两个相似四边形的相似比是1:3,则它们的周长比是1:3,面积比是1:6;③同一平面内垂直于同一直线的两条直线互相平行;④对角线相等且互相垂直的平行四边形是正方形.其中真命题有( )
- A ①③
- B ①④
- C ③④
- D ②③④
- 参考答案:C
- 您的答案:
参考解析:
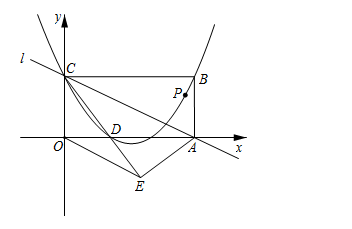
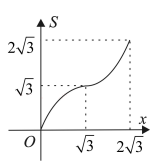
如图,矩形ABCD各边中点分别是E、F、G、H,AB=2√3,BC=2,M为AB上一动点,过点M作直线l⊥AB,若点M从点A开始沿着AB方向移动到点B即停(直线l随点M移动),直线l扫过矩形内部和四边形EFGH外部的面积之和记为S.设AM=x,则S关于x的函数图象大致是( )
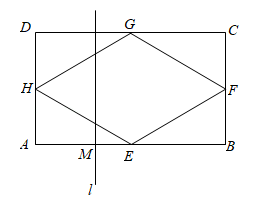
-
A

-
B
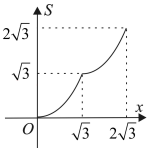
-
C
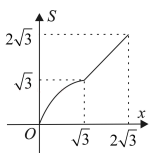
-
D
- 参考答案:D
- 您的答案:
参考解析:

- 参考答案:
- 您的答案:
参考解析:
某公司开展“爱心公益”活动,将价值16000元的物品捐赠给山区小学,数据16000用科学记数法表示为________.
- 参考答案:
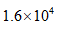
- 您的答案:
参考解析:
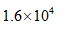
如图,是一组数据的折线统计图,则这组数据的中位数是____.
- 参考答案:9
- 您的答案:
参考解析:
9
实数√105的整数部分是______.
- 参考答案:10
- 您的答案:
参考解析:
10
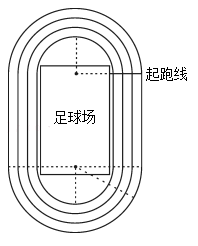
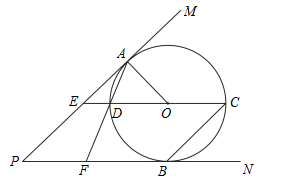
数学活动小组为测量山顶电视塔的高度,在塔的椭圆平台遥控无人机.当无人机飞到点P处时,与平台中心O点的水平距离为15米,测得塔顶A点的仰角为30°,塔底B点的俯角为60°,则电视塔的高度为_________米.
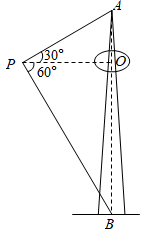
- 参考答案:20√3
- 您的答案:
参考解析:
20√3
如图,△ABC中,AB=AC,∠B=72°,∠ACB的平分线CD交AB于点D,则点D是线段AB的黄金分割点.若AC=2,则BD=______.
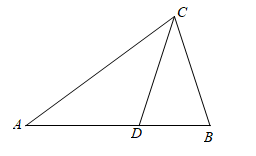
- 参考答案:
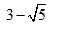
- 您的答案:
参考解析:
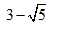
- 参考答案:
- 您的答案:
参考解析:

- 参考答案:
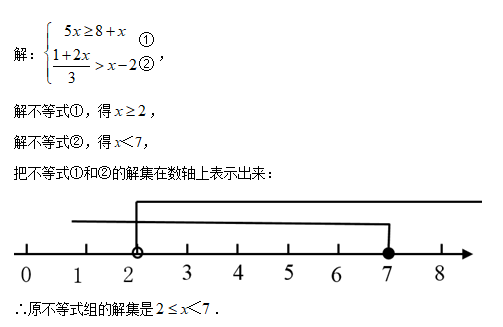
- 您的答案:
参考解析:
如图,O为坐标原点,直线l⊥y轴,垂足为M,反比例函数y=k/x(k≠0)的图象与l交于点A(m,3),△AOM的面积为6
(1)求m、k的值;
(2)在x轴正半轴上取一点B,使OB=OA,求直线AB的函数表达式.
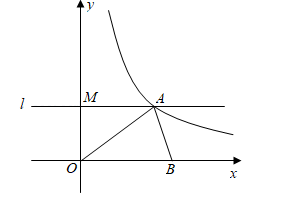
- 参考答案:

- 您的答案: