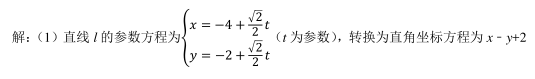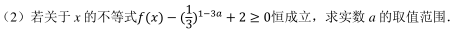已知集合 A={x∈N|2x﹣ 7≤0}, B={x|x 2 ﹣ 2x﹣ 3≤0}, 则 A∩ B=()
- A {x|0<x≤3}
- B {0, 1, 2, 3}
- C {x| − 1 ≤ x ≤7/2 }
- D {1, 2, 3}
- 参考答案:B
- 您的答案:
参考解析:
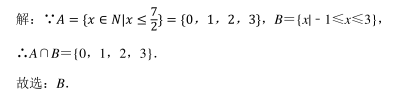
复数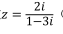 (i为虚数单位)的虚部是
(i为虚数单位)的虚部是

- A A
- B B
- C C
- D D
- 参考答案:C
- 您的答案:
参考解析:
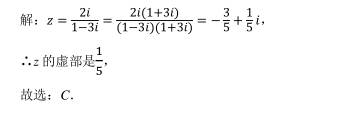

- A a>b>c
- B c>b>a
- C b>a>c
- D b>c>a
- 参考答案:C
- 您的答案:
参考解析:

某校某学习小组调查研究“学生线上学习时智能手机对学习成绩的影响”, 得到了如下样本数据:
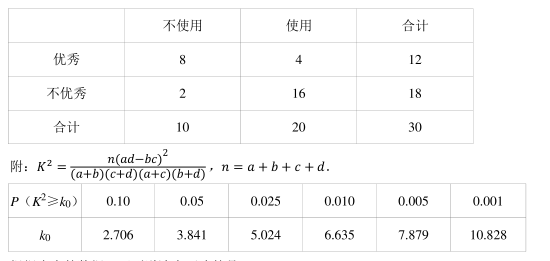
根据表中的数据, 下列说法中正确的是()
- A 有 99.5%的把握认为中学生使用手机对学习无影响
- B 有 99.5%的把握认为中学生使用手机对学习有影响
- C 在犯错误的概率不超过 0.001 的前提下认为中学生使用手机对学习无影响
- D 在犯错误的概率不超过 0.001 的前提下认为中学生使用手机对学习有影响
- 参考答案:B
- 您的答案:
参考解析:

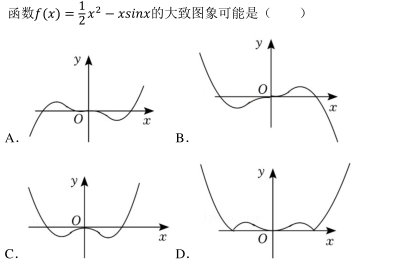
- A A
- B B
- C C
- D D
- 参考答案:C
- 您的答案:
参考解析:

某校迎新晚会上有 6 个节目, 考虑整体效果, 对节目演出顺序有如下要求: 节目甲必须排在第三位, 且节目丙、 丁必须排在一起, 则该校迎新晚会节目演出顺序的编排方案共有()
- A 36 种
- B 48 种
- C 72 种
- D 120 种
- 参考答案:A
- 您的答案:
参考解析:


- A A
- B B
- C C
- D D
- 参考答案:C
- 您的答案:
参考解析:

已知函数 y=[x]称为高斯函数, 其中[x]表示不超过实数 x 的最大整数, 执行如图程序框图, 则输出的 S 值为()
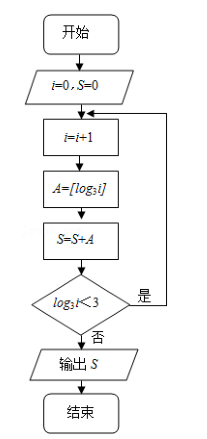
- A 42
- B 43
- C 44
- D 45
- 参考答案:D
- 您的答案:
参考解析:


- A A
- B B
- C C
- D D
- 参考答案:D
- 您的答案:
参考解析:



- A 2√5 − 1
- B 2
- C 3
- D 4
- 参考答案:B
- 您的答案:
参考解析:

已知关于 x 的方程 x﹣ lna=2ln|x|有三个不等的实数根, 则实数 a 的取值范围是()
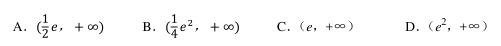
- A A
- B B
- C C
- D D
- 参考答案:B
- 您的答案:
参考解析:

已知正方体 ABCD﹣ A 1 B 1 C 1 D 1 的棱长为 a, 点 E, F, G 分别为棱 AB, AA 1 , C 1 D 1 的中点, 下列结论中正确的个数是()
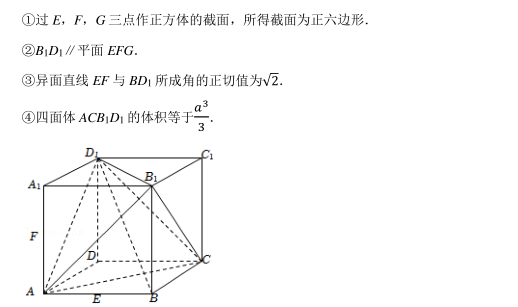
- A 1
- B 2
- C 3
- D 4
- 参考答案:B
- 您的答案:
参考解析:


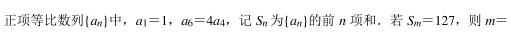
- 参考答案:7
- 您的答案:
参考解析:

如图所示, 在边长为 1 的正方形 OABC 中任取一点 P, 则点 P 恰好取自阴影部分(由对角线 OB 及函数 y=x3 围成) 的概率为
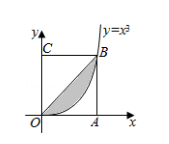
- 参考答案:1/4
- 您的答案:
参考解析:

已知 P 为球 O 球面上一点, 点 M满足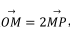 过点 M与 OP 成 30° 的平面截球 O,截面的面积为 16π, 则球 O 的表面积为
过点 M与 OP 成 30° 的平面截球 O,截面的面积为 16π, 则球 O 的表面积为
- 参考答案:72π
- 您的答案:
参考解析:

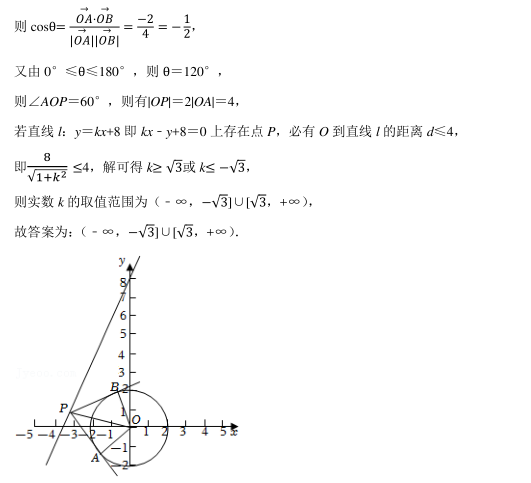
在平面直角坐标系 xOy 中, 已知直线 l: y=kx+8 上存在点 P, 过点 P 作圆 O: x 2 +y 2 =4的切线, 切点分别为 A(x 1 , y 1 ), B(x 2 , y 2 ), 且 x 1 x 2 +y 1 y 2 =﹣ 2, 则实数 k 的取值范围为
- 参考答案:(﹣ ∞, −√3]∪ [√3, +∞)
- 您的答案:
参考解析:
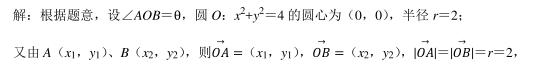
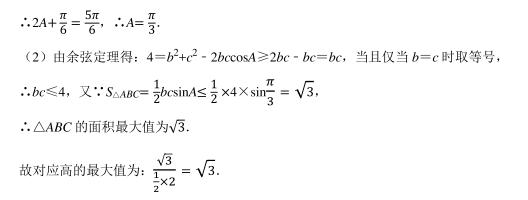
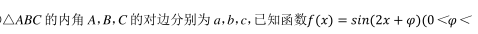

- 参考答案:
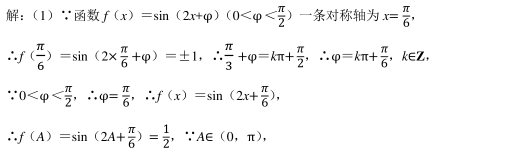
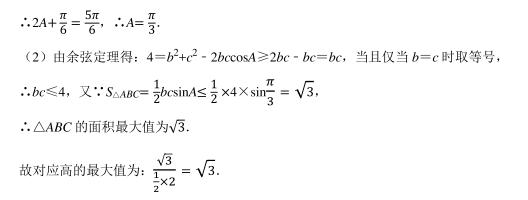
- 您的答案:
参考解析:

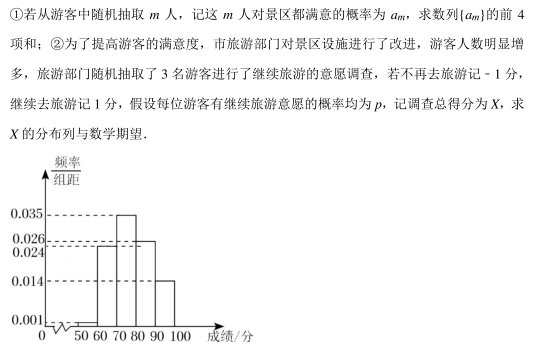
为了了解游客对景区的满意度, 市旅游部门随机对景区的 100 名游客进行问卷调查(满分 100 分), 这 100 名游客的评分分别落在区间[50, 60), [60, 70), [70, 80),[80, 90), [90, 100]内, 且游客之间的评分情况相互独立, 得到统计结果如频率分布直方图所示.
(1) 求这 100 名游客评分的平均值(同一区间的数据用该区间数据的中点值为代表);
(2) 视频率为概率, 规定评分不低于 80 分为满意, 低于 80 分为不满意, 记游客不满意的概率为 p.
- 参考答案:


- 您的答案:
参考解析:

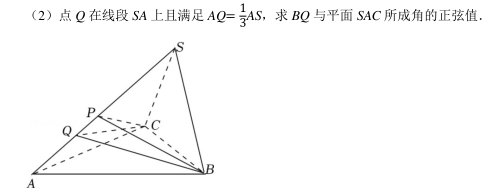
如图, 三棱锥 S﹣ ABC 中, 底面 ABC 和侧面 SBC 都是等边三角形, BC=2,SA= √6.
(1) 若 P 点是线段 SA 的中点, 求证: SA⊥平面 PBC;
- 参考答案:


- 您的答案: