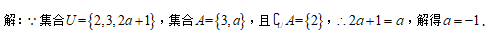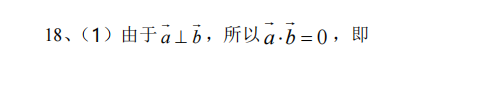已知椭圆M:x2/a2+y2/b2=1(a>b>0)双曲线N:x2/m2-y2/n2=1,若双曲线N的两条斩近线与椭圆M的四个交点及椭圆M的两个焦点恰为--个正六边形的顶点则椭圆M的焦距与长轴长的比值为____
9、现有m(m≥2)行数表如下:
第一行:2m-1,2m-2,2m-3,2m-4.......21,20
第二行: 2m-2,2m-3,2m-4.......21,20
第三行: 2m-3,2m-4.......21,20
第m-1行:21,20
第m行: 20
按照上述方式从第一行写到第 m行(写下的第n个数记作an )得到有穷数列{an},其前n项和为Sn,若S2018 存在,则S2018的最小值为
气象意义上从春季进入夏季的标志为连续5天的日平均温度均不低于22C.现有甲、乙、丙三地连续5天的日平均温度的记录数据:(记录数据都是正整数)
①甲地5个数据的中位数为24,众数为22;
②乙地5个数据的中位数为27,总体均值为24;
③丙地5个数据中有-个数据是32,总体均值为26,总体方差为10. 8.
则肯定进入夏季的地区有____
在实数集R中,我们定义的大小关系“>“为全体实数排了一个“序”类似地,我们在复数集C上也可以定义一个称为“序”的关系,记为“>”定义如下对于任意两个复数:

设{an}为等比数列,则“对于任意的m∈N,am+2>an”是“{an}为递增数列”的()
- A 充分而不必要条件
- B 必要而不充分条件
- C 充分必要条件
- D 既不充分也不必要条件
- 参考答案:C
- 您的答案:
参考解析:

已知函数f(x)=sinx+cosx,将f(x)图象上所有点的横坐标缩短到原来的1/2倍,纵坐标保持不变,得到函数y=g(x)的图象,若g(x1)g(x2)=-2,则▏x1-x2▕的最小值为
- A π/2
- B π
- C 2π
- D 4π
- 参考答案:A
- 您的答案:
参考解析:
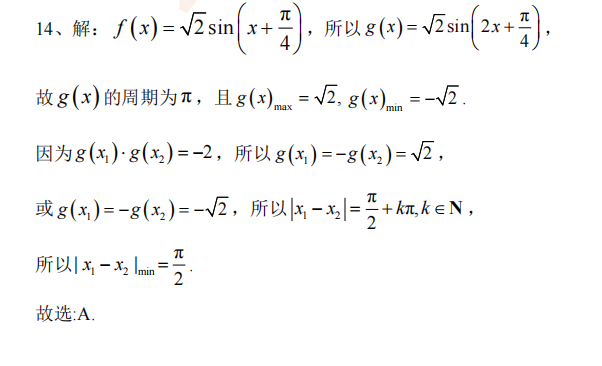
已知在△ABC中,P0是边AB上的一个定点,
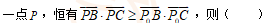
- A B=π/2
- B A=π/2
- C AB=AC
- D AC=BC
- 参考答案:D
- 您的答案:
参考解析:

有一容积为a3cm3的正方体容器ABCD-A1B1C1D1,在棱AB、BB1和面对角线BC1的重点各有一小孔E、F、G,若此容器可以任意防止,则其可装水的最大容积是()
-
A
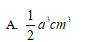
-
B
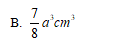
-
C
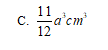
-
D
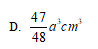
- 参考答案:C
- 您的答案:
参考解析:
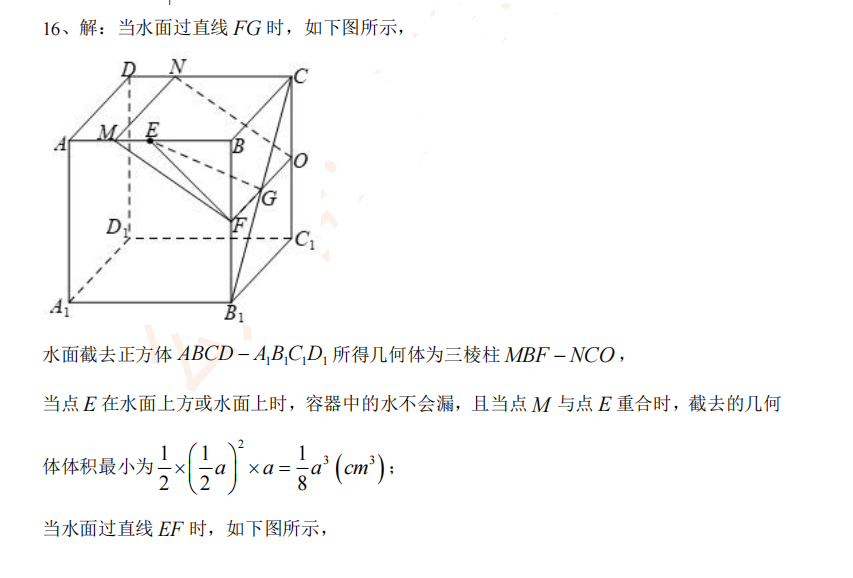
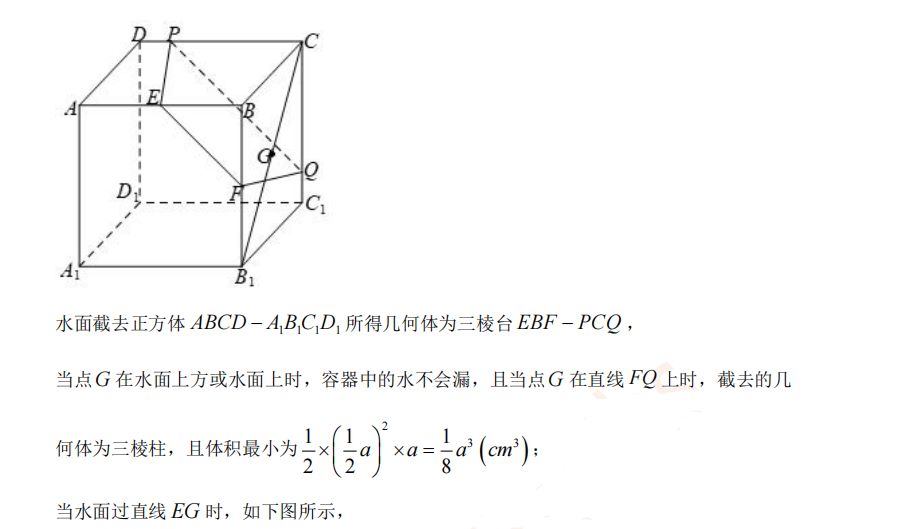


已知f(x)=kx+2,不等式▕f(x)▕<3的解集为(-1,5),不等式x/f(x)≥1的解集为A。
(1)求实数K的值,以及集合A;
(2)若B={x▏x2-(2a+1)x+a(a+1)<0}(a∈R),且A∩B=Φ,求a的取值范围.
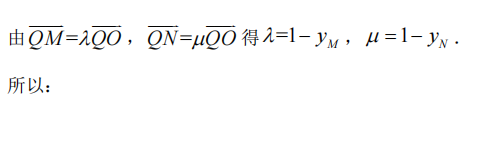
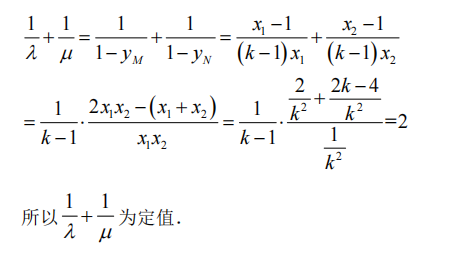
已知抛物线C:y2=2px经过点p(1,2).过点Q(0,1)的直线ι与抛物线C有两个不同交点A,B,且直线PA交y轴于M,直线PB交y轴于N。
(1)求直线ι的斜率的取值范围;
(2)设O为原点,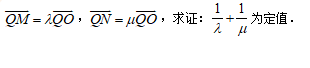
如图,空间直角坐标系中,四棱锥P-OABC的底面是边长为√2的正方形,且底面在xOy平面内,点B在y轴正半轴上,PB⊥平面OABC,侧棱OP与底面所成角为45°
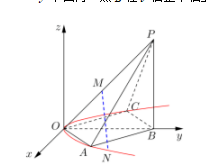
(1)若N(x,y,0)是顶点在原点,且过A、C两点的抛物线上的动点,试给出x与y满足的关系式;
(2)若M是棱OP上的一个定点,它到平面OABC的距离为a (0<a<2 ),写出M、N两点之间的距离d(x),并求d(x)的最小值;
(3)是否存在一个实数a (0<a<2 ),使得当d(x)取得最小值时,异面直线MN与OB互相垂直?请说明理由;

已知无穷数列{an},对于m∈N,若{an}同时满足以下三个条件,则称数列{an}具有性质P(m).
条件①: a>0 (n=1, 2; ... );
条件②:存在常数T>0,使得a≤T (n=1, 2, ..);
条件③: an+an-1=man+2(n=1,2, ... )。
(1)若an=5+4x(-1/2)" (n=1, 2,..且数列{an}具有性质P (m), 直接写出m的值和一个T的值;
(2)是否存在具有性质P (1)的数列{an}?若存在,求数列{an}的通项公式;若不存在,说明理由;
(3)设数列{an}具有性质P (m), 且各项均为正整数,求数列{an}的通项公式.