把 30 分解质因数,正确的做法是( )
- A 30=1×2×3×5
- B 2×3×5=30
- C 30=2×3×5
- 参考答案:C
- 您的答案:
参考解析:
解:A,30=1×2×3×5,其中 1 既不是质数,也不是合数,所以不正确;
B,2×3×5=30,此题是求几个数的积的运算,不是合数分解质因数;
C,30=2×3×5,符合要求,所以正确;
故选 C.
一杯纯牛奶,喝去1/5 ,加清水摇匀,再喝去1/2 ,再加清水,这时杯中牛奶与水的比是( )
- A 3:7
- B 2:3
- C 2:5
- D 1:1
- 参考答案:B
- 您的答案:
参考解析:

一个三角形中,最大的一个角一定不小于( )。
- A 50°
- B 60°
- C 70°
- D 90°
- 参考答案:B
- 您的答案:
参考解析:
当三个内角相等的时候,最大的内角最小,此时每个角都是 60°;
所以最大的一个角一定不小于 60°;
故答案选:B。
甲数是乙数的2/3 ,乙数是丙数的4/5 ,甲、乙、丙三数的比是( )
- A 4:5:8
- B 4:5:6
- C 8:12:15
- D 12:8:15
- 参考答案:C
- 您的答案:
参考解析:

要使 30:(9﹣3x)有意义,x 不能是( )
- A 0
- B 1
- C 2
- D 3
- 参考答案:D
- 您的答案:
参考解析:

下面各交通标志是轴对称图形的是( )

- A A
- B B
- C C
- 参考答案:A
- 您的答案:
参考解析:
已知 M=4322×1233,N=4321×1234,下面结论正确的是( )
- A M>N
- B M=N
- C M<N
- D 无法判断
- 参考答案:C
- 您的答案:
参考解析:
试题分析:N=4321×1234=(4322﹣1)×(1233+1)=4322×1233+4322﹣1233﹣1=M+3088,
所以 M<N,据此判断即可.
解:N=4321×1234
=(4322﹣1)×(1233+1)
=4322×1233+4322﹣1233﹣1
=M+3088,
所以 M<N.
故选:C.
2014x=2013y,则 x:y=( )
- A 2014:2013
- B 2013:2014
- C 2014:4027
- D 4027:2014
- 参考答案:B
- 您的答案:
参考解析:
试题分析:根据比例的性质,把所给的等式 2014x=2013y,改写成一个外项是 x,一个内项是 y 的比例,则和 x 相乘的数 2014 就作为比例的另一个外项,和 y 相乘的数 2013 就作为比例的另一个内项,据此写出比例即可.
解:如果 2014x=2013y,那么 x:y=2013:2014.
故选:B.
一个长方形的长为 a,宽为 b(a>b),若长增加 20%,宽减少 20%,则它的面积( )
- A 增加 20%
- B 减少 20%
- C 减少 4%
- D 不变
- 参考答案:C
- 您的答案:
参考解析:
解:[a×(1+20%)]×[b×(1﹣20%)] =[a×120%]×[b×80%] =96%ab
ab﹣96%ab=4%ab
故选 C.
有一根 1 米长的木条,第一次据掉它的1/3 ,第二次据掉余下的1/4 ,第三次据掉余下的 1/5,…,这样下去,最后一次据掉余下的 1/8,这根木条最后剩( )
- A 1/3米
- B 1/4米
- C 1/5米
- D 1/6米
- 参考答案:B
- 您的答案:
参考解析:
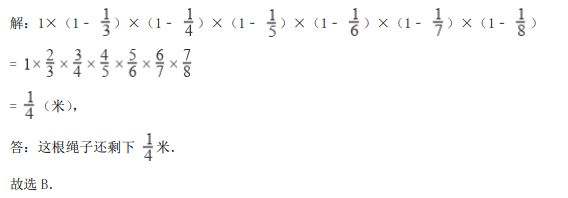
我国领土的面积是( )
- A 960 万
- B 960 万平方米
- C 960 万平方千米
- 参考答案:C
- 您的答案:
参考解析:
试题分析:根据生活经验、对面积单位和数据大小的认识,可知我国领土的面积是 960 万平方千米.
解:我国领土的面积是 960 万平方千米;
故答案为:C.
洋洋爸爸带他去划船,游到水中央时,爸爸将放在船上的一堆石头扔入水中,水面会( )
- A 上升
- B 下降
- C 没变化
- 参考答案:B
- 您的答案:
参考解析:
试题分析:载着石头的时候,船和石头的总重力等于浮力,G 总=F 浮,静止;当把石头扔到水总时,石头所受的重力将大于其浮力(所以石头向下运动,沉到水底),此时 G 总'>F 浮,又因为 F 浮=P 液小 GV 排,所受浮力减小,故排开水体积减小(此处只能为 V 排引起,小 G与 P 液均不改变),所以水面会下降,据此解答即可.
解:载着石头的时候,船和石头的总重力等于浮力,G 总=F 浮,静止;当把石头扔到水总时,石头所受的重力将大于其浮力(所以石头向下运动,沉到水底),此时 G 总'>F 浮,又因为 F 浮=P 液小 GV 排,所受浮力减小,故排开水体积减小(此处只能为 V 排引起,小 G 与 P 液均不改变),所以水面会下降.
故选:B
最早精确计算出圆周率的是我国古代数学家( )
- A 刘薇
- B 祖冲之
- C 秦九昭
- 参考答案:B
- 您的答案:
参考解析:
试题分析:约在 1500 年前,我国古代数学家祖冲之计算出圆周率应在 3.1415926 和3.1415927 之间,成为世界上第一个把圆周率的值精确到 7 位小数的人,比国外数学家至少要早 1000 年.
解:约在 1500 年前,对π值计算最精确的是我国古代数学家祖冲之.
故选:B.
24 小时 PM2.5 平均值超标准值为 100﹣150,则空气质量等级为( )
- A 优
- B 轻度污染
- C 严重污染
- 参考答案:B
- 您的答案:
参考解析:
试题分析:根据 PM2.5 检测网的空气质量新标准,24 小时平均值标准值分布如下:空气质量等级 24 小时 PM2.5 平均值标准值
优 0﹣35
良 35﹣75
轻度污染 75﹣115
中度污染 115﹣150
重度污染 150﹣250
严重污染 大于 250 及以上
解;根据标准可知 100﹣150 应属于轻度污染和中度污染之间.
故选:B
比 1 小的数一定是小数
- 对 正确。
- 错 错误。
- 参考答案:
错误
- 您的答案:
参考解析:
试题分析:比 1 小的数还有“0”和负整数,据此解答即可.
解:由分析可知,比 1 小的数一定是小数,说法错误;
任意翻阅 2014 年的台历,翻到星期一的可能性比翻到 1 号的可能性大
- 对 正确。
- 错 错误。
- 参考答案:
正确
- 您的答案:
参考解析:
试题分析:每七天有一个星期一,每个月有一个 1 号,所以任意翻阅 2014 年的台历,翻到星期一的可能性比翻到 1 号的可能性大,据此解答即可.
解:每七天有一个星期一,每个月有一个 1 号,所以任意翻阅 2014 年的台历,翻到星期一的可能性比翻到 1 号的可能性大,因此题中说法正确
图上距离总比实际距离小
- 对 正确。
- 错 错误。
- 参考答案:
错误
- 您的答案:
参考解析:
试题分析:图上距离与实际距离的比是比例尺,但图上距离并不是都比实际距离小,比如一些精密的仪器,它们的实际长度比较小,但在画图时,为了观察和操作方便,就需要图上的距离比实际距离大一些,由此即可判断正误.
解:因为一些精密的仪器,它们的实际长度比较小,但在画图时,为了观察和操作方便,需要画的大一些,所以,图上距离并不总是比实际距离小,
故答案为:错误
用“四舍五入”法取近似值,约等于 0.5 的两位小数中最大的是 0.49
- 对 正确。
- 错 错误。
- 参考答案:
错误
- 您的答案:
参考解析:
试题分析:要考虑 0.5 是一个两位数的近似数,有两种情况:“四舍”得到的 0.5 最大是 0.54,“五入”得到的 0.5 最小是 0.45,由此解答问题即可.
解:用“四舍五入”法取近似值,约等于 0.5 的两位小数中最大的是 0.54;
圆柱的体积是圆锥体积的 3 倍
- 对 正确。
- 错 错误。
- 参考答案:
错误
- 您的答案:
参考解析:
试题分析:我们知道,一个圆柱的体积是与它等底等高的圆锥体积的 3 倍,原题没有注明“等底等高”或其它的条件,只说“圆柱的体积是圆锥体积的 3 倍”是错误的.
解:由于圆柱、圆锥的体积公式中都有底面积和高两个未知的量,原题没有对这两个量加以“等底等高”或其它条件的限制,所以不能说“圆柱的体积是圆锥体积的 3 倍”;故答案为:错误
所有偶数的最大公因数是 2
- 对 正确。
- 错 错误。
- 参考答案:
错误
- 您的答案:
参考解析:
试题分析:根据偶数的意义,在自然数中,是 2 的倍数的数叫做偶数.再根据公因数、最大公因数的意义,几个数公有的因数叫做这几个数的公因数,其中最大的一个是它们最大公因数.据此判断即可.
解:因为 2 是偶数,而 2 的因数中最大的是 2,所以所有偶数(0 除外)的最大公因数是 2.所有偶数的最大公因数是 2 的说法错误,应该是 0 除外的偶数.
方程一定是等式,但等式不一定是方程
- 对 正确。
- 错 错误。
- 参考答案:
正确
- 您的答案:
参考解析:
解:根据方程的定义可以知道,方程是含有未知数的等式,但是等式不一定都含有未知数,所以这个说法是正确的.
故答案为:正确
再一次植树活动中,成活了 100 课,10 课没成活,所以成活率为 90%
- 对 正确。
- 错 错误。
- 参考答案:
错误
- 您的答案:
参考解析:

小于 90 度的角是锐角
- 对 正确。
- 错 错误。
- 参考答案:
正确
- 您的答案:
参考解析:
试题分析:根据锐角的含义:大于 0°小于 90°的角叫做锐角;进行判断即可.
解:根据锐角的定义:小于 90 度的角是锐角;
甲、乙两数是正整数,如果甲数的 5/6恰好是乙数的1/4 ,则甲、乙两数和的最小值是 13
- 对 正确。
- 错 错误。
- 参考答案:
正确
- 您的答案:
参考解析:

停车场共有 24 辆车,其中有 4 轮车和 3 轮车,这些车共有 86 个轮子,那么 3 轮车有______辆
- 参考答案:10
- 您的答案:
参考解析:
假设 24 辆全部为 4 轮车,则一共有轮子 24×4=96 个,比实际 86 个多了 96-86=10 个,因为1 辆 3 轮车比 1 辆 4 轮车少 4-3=1 个轮子,因此三轮车的数量为 10(辆)。
列式为:(24×4-86)÷(4-3)=10÷1=10(辆)
定 义 一 种 新 运 算 “△” 满 足 : 8△3=8+9+10=27 ,7△4=7+8+9+10=34,6△5=6+7+8+9+10=40,求 1△10.
一部书稿,甲单独打字需 60 天完成,乙单独打字需 50 天完成,已知甲每周日休息,乙每周六、周日休息。如果两人合作,从 2014 年 4 月 21 日(周一)开始打字,那么几月几日可以完成这部书稿?
如图,ABCD 是直角梯形,ACFE 是长方形,已知 BC﹣AD=4cm,CD=6cm,梯形面积是 60cm2,求阴影部分的面积
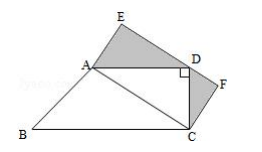
- 参考答案:
答:阴影部分的面积是 24cm2
- 您的答案:
参考解析:
解:BC+AD=(60×2)÷6=20(cm)…①,
BC﹣AD=4cm…②,
由①②,可得
BC=12(cm),AD=8cm;
因为三角形 ACD 的面积等于 AC 的乘以 CF,再除以 2,
所以三角形 ACD 的面积等于长方形 ACFE 的面积的一半,
因此阴影部分的面积等于三角形 ACD 的面积,
则阴影部分的面积=AD×CD÷2=8×6÷2=24(cm2).
成都青年旅行社“五一”推出甲、乙两种优惠方案:
甲:成都一日游,大人每位全票 80 元,小朋友四折
乙:成都一日游,团体 5 人以上(含 5 人)每位六折
(1)李老师带 5 名小朋友游览,选哪种方案省钱?
(2) 李老师和王老师带 4 名小朋友游览,选哪种方案省钱?
(3) 张三、王五两位小朋友及各自的父母 6 人游览,选哪种方案省钱?
- 参考答案:
(1)甲方案省钱 (2)甲乙方案都可以 (3)乙方案省钱.
- 您的答案:
参考解析:
(1)李老师带 5 名小朋友游览,即 1 个大人和 5 个小朋友,共计 6 人
甲方案:1×80+5×80×0.4=240 元
乙方案:(1+5)×80×0.6=288 元
240<288,因此甲方案省钱.
(2)李老师和王老师带 4 名小朋友游览,即 2 个大人和 4 个小朋友,共计 6 人
甲方案:2×80+4×80×0.4=288 元
乙方案:(2+4)×80×0.6=288 元
因此甲乙方案都可以选.
(3)张三、王五两位小朋友及各自的父母 6 人游览,即 4 个大人和 2 个小朋友,共计 6 人
甲方案:4×80+2×80×0.4=384 元
乙方案:(4+2)×80×0.6=288 元
384>288,因此乙方案省钱.
答:(1)甲方案省钱;(2)甲乙方案都可以;(3)乙方案省钱
体育商店买 100 个足球和 50 个排球,共有 5600 元,如果将每个足球加价1/10和每个排球减价1/10,全部售出后共收入 6040 元,问买进时一个足球和排球是多少元?
环绕小山一周的公路长 1920 米,甲、乙两人沿公路竞走,两人同时同地出发,反方向行走,甲比乙走得快,12 分钟后两人相遇.如果两人每分钟多走 16 米,则相遇地点与前次相差 20 米.
(1)求甲乙两人原来的行走速度.
(2)如果甲、乙两人各以原速度同时同地出发,同向行走,则甲在何处第二次追上乙?
- 参考答案:
(1)答:甲原来的速度是 90 米/分,乙原来的速度是 70 米/分;
(2)答:甲在出发点第二次追上乙.
- 您的答案:
参考解析:
解:(1)甲乙原来的速度之和是:1920÷12=160(米),
提高速度之后的速度之和是:160+16+16=192(米),
所以提高速度之后二人相遇的时间是:1920÷192=10(分钟),
设甲原来的速度是 x 米/分,则提高速度后,甲的速度是(x+16)米/分,根据题意可得方程:
12x﹣10(x+16)=20,
12x﹣10x﹣160=20,
2x=180,
x=90,
则乙原来的速度是:160﹣90=70(米/分),
答:甲原来的速度是 90 米/分,乙原来的速度是 70 米/分;
(2)1920×2÷(90﹣70)
=1920×2÷20
=192(分),
192×90÷1920=9,说明正好在出发点.
答:甲在出发点第二次追上乙


