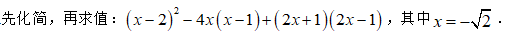下列各数中,是负数的是( )
- A -1
- B 0
- C 0.2
- D 1/2
- 参考答案:A
- 您的答案:
参考解析:
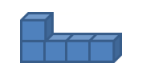
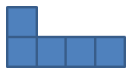
如图所示,该几何体的俯视图是( )
-
A

-
B
-
C

-
D

- 参考答案:C
- 您的答案:
参考解析:
根据俯视图是从上边看的到的视图,可得答案.
【详解】解:从上边可以看到4列,每列都是一个小正方形,故C符合题意;
故选C.
【点睛】本题考查了简单组合体的三视图,从上边看的到的视图是俯视图.掌握俯视图的含义是解题的关键.
下列运算不正确的是( )
-
A
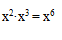
-
B
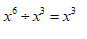
-
C
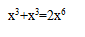
-
D
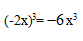
- 参考答案:B
- 您的答案:
参考解析:
如图,数轴上的点A、B分别对应实数a、b,下列结论中正确的是

- A a>b
- B |a|>|b|
- C -a<b
- D a+b>0
- 参考答案:B
- 您的答案:
参考解析:
下列关于x的方程有两个不相等实数根的是( )
-
A
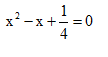
-
B
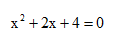
-
C
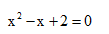
-
D
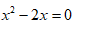
- 参考答案:D
- 您的答案:
参考解析:
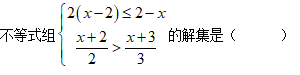
-
A
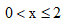
-
B
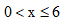
-
C
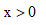
-
D
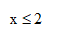
- 参考答案:A
- 您的答案:
参考解析:
在四张背面完全相同的卡片上分别印有正方形、正五边形、正六边形、圆的图案,现将印有图案的一面朝下,混合后从中随机抽取两张,则抽到卡片上印有的图案都是中心对称图形的概率为( )
- A 1/4
- B 1/3
- C 1/2
- D 3/4
- 参考答案:C
- 您的答案:
参考解析:

-
A
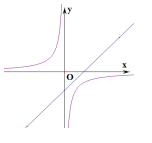
-
B
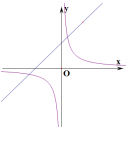
-
C
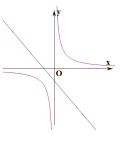
-
D
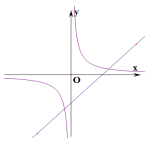
- 参考答案:D
- 您的答案:
参考解析:
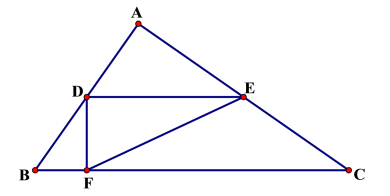
如图,在△ABC中,∠A=90°,D是AB的中点,过点D作BC的平行线,交AC于点E,作BC的垂线交BC于点F,若AB=CE,且△DFE的面积为1,则BC的长为( )
-
A
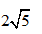
- B 5
-
C
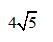
- D 10
- 参考答案:A
- 您的答案:
参考解析:
某林业部门统计某种幼树在一定条件下的移植成活率,结果如下表所示:
移植总数(n) | 200 | 500 | 800 | 2000 | 12000 |
成活数(m) | 187 | 446 | 730 | 1790 | 10836 |
成活的频率 (m/n)
| 0.935 | 0.892 | 0.913 | 0.895 | 0.903 |
- 参考答案:0.9
- 您的答案:
参考解析:
【分析】
由题意根据概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率进行分析即可.
【详解】解:概率是大量重复实验的情况下,频率的稳定值可以作为概率的估计值,即次数越多的频率越接近于概率,
∴这种幼树移植成活率的概率约为0.9.
故答案为:0.9.
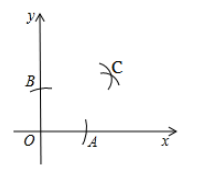
如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取OA、OB,使OA=OB;再分别以点A、B为圆心,以大于1/2AB长为半径作弧,两弧交于点P.若点C的坐标为(a,2a-3),则a的值为________.
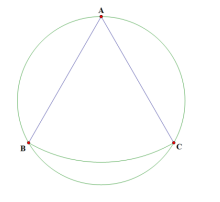
如图,圆的半径是2,扇形BAC的圆心角为60°,若将扇形BAC剪下,围成一个圆锥,则此圆锥的底面圆的半径为_____.
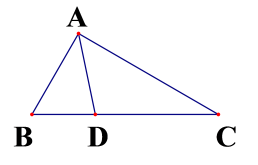
如图,在△ABC中,∠A=90°,∠B=60°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为_____.
如图,四边形ABCD是平行四边形,DE//BF,且分别交对角线AC于点E,F,连接BE,DF.
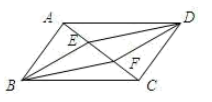
(1)求证:AE=CF;
(2)若BE=DE,求证:四边形EBFD为菱形.
为了解某校九年级学生的体质健康状况,随机抽取了该校九年级学生的10%进行测试,
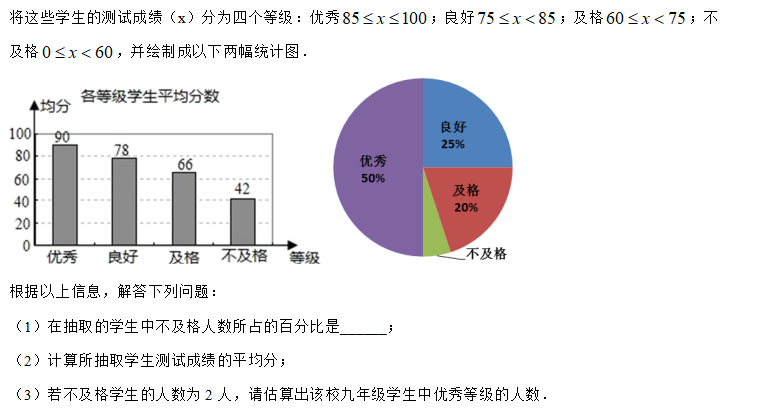
如图,为测量建筑物CD的高度,在点A测得建筑物顶部D点的仰角是22°,再向建筑物CD前进30米到达B点,测得建筑物顶部D点的仰角为58°(A,B,C在同一直线上),求建筑物CD的高度.(结果保留整数)
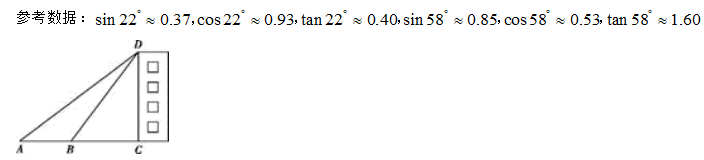
某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
- 参考答案:
【答案】(1)A款保温杯的售价为30元,B款保温杯的售价为40元;(2)进货80个A款保温杯,40个B款保温杯,利润最大,为1440元.
【解析】
【分析】
(1)设:A款保温杯的售价为x元,B款保温杯的售价为(x+10)元;利用数量相等列方程求解即可;(2)设进货A款保温杯m个,B款保温杯(120-m)个,总利润为w,根据题意得出函数关系式,同时列出不等式组得到m的范围,再利用一次函数的性质得到答案.

- 您的答案: