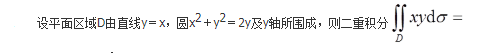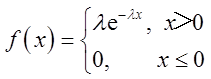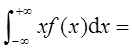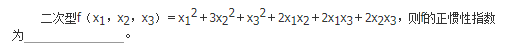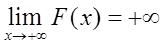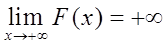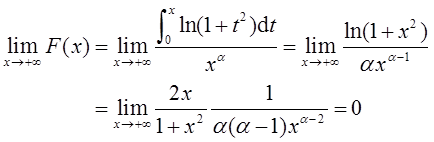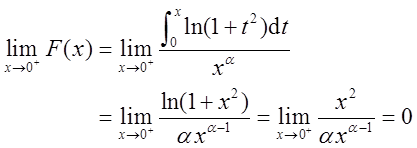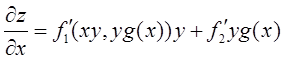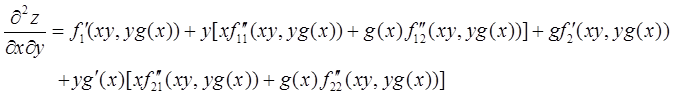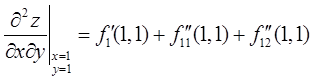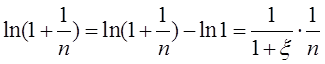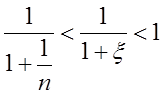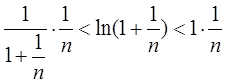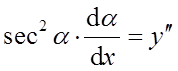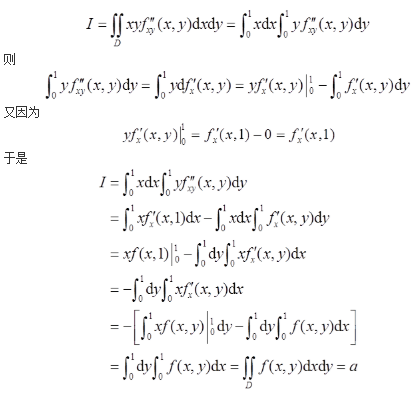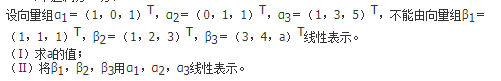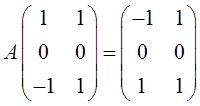设
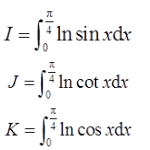
则I,J,K的大小关系为( )。
- A I<J<K
- B I<K<J
- C J<I<K
- D K<J<I
- 参考答案:B
- 您的答案:
参考解析:
在(0,π/4)上,sinx<cosx<1<cotx从而lnsinx<lncosx<lncotx,即
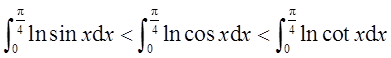
已知当x→0时,函数f(x)=3sinx-sin3x与cxk是等价无穷小,则( )。
- A k=1,c=4
- B k=1,c=-4
- C k=3,c=4
- D k=3,c=-4
- 参考答案:C
- 您的答案:
参考解析:
由题意,f(x)与是cxk等价无穷小,由等价无穷小的定义,有
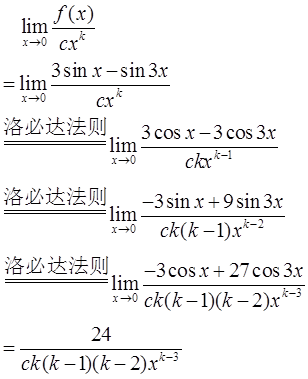
从而k=3,ck(k-1)(k-2)=24;即k=3,c=4。
函数f(x)=ln|(x-1)(x-2)(x-3)|的驻点个数为( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:

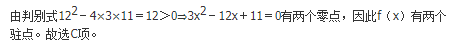
设函数f(x),g(x)均有二阶连续导数,满足f(0)>0,g(0)<0,f′(0)=g′(0)=0,则函数z=f(x)g(y)在点(0,0)处取得极小值的一个充分条件是( )。
- A f″(0)<0,g″(0)>0
- B f″(0)<0,g″(0)<0
- C f″(0)>0,g″(0)>0
- D f″(0)>0,g″(0)<0
- 参考答案:A
- 您的答案:
参考解析:
由z=f(x)g(y)得
?z/?x=f′(x)g(y)
?z/?y=f(x)g′(y)
B=?2z/?x?y=f′(x)g′(y)
A=?2z/?x2=f″(x)g(y)
C=?2z/?y2=f(x)g″(y)
在(0,0)点,A=f″(0)g(0),B=f′(0)g′(0)=0,C=f(0)g″(0)。由
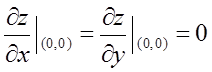
可得,(0,0)是z=f(x)g(y)可能的极值点。若z=f(x)g(y)在(0,0)有极小值。由AC-B2>0且A>0?f″(0)<0,g″(0)>0故选A项。
设函数f(x)在x=0处可导,且f(0)=0,则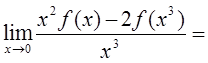 ( )。
( )。
- A -2f′(0)
- B -f′(0)
- C f′(0)
- D 0
- 参考答案:B
- 您的答案:
参考解析:
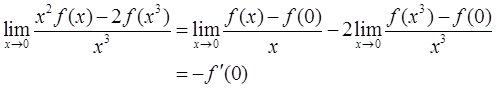
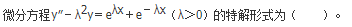
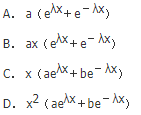
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

设A为3阶矩阵,将A的第2列加到第1列得矩阵B,再交换B的第2行与第3行得单位矩阵。记

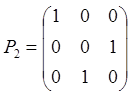
则A=( )。
- A P1P2
- B P1-1P2
- C P2P1
- D P2P1-1
- 参考答案:D
- 您的答案:
参考解析:
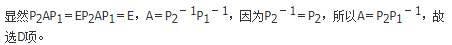
设A=(α1,α2,α3,α4)是4阶矩阵,A*为A的伴随矩阵。若(1,0,1,0)T是方程组Ax=0的一个基础解系,则A*x=0的基础解系可为( )。
- A α1,α3
- B α1,α2
- C α1,α2,α3
- D α2,α3,α4
- 参考答案:D
- 您的答案:
参考解析:
因为Ax=0基础解系含一个线性无关的解向量,所以r(A)=3,于是r(A*)=1,故A*x=0基础解系含3个线性无关的解向量。又A*A=|A|E=0且r(A)=3,所以A的列向量组中含A*x=0的基础解系。
因为(1,0,1,0)T是方程组Ax=0的基础解系,所以α1+α3=0,故α1,α2,α4或α2,α3,α4线性无关,显然α2,α3,α4为A*x=0的一个基础解系,故选D项。
已知函数
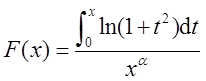
设
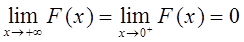
试求α的取值范围。
设函数z=f(xy,yg(x)),其中函数f具有二阶连续偏导数,函数g(x)可导且在x=1处取得极值g(1)=1,求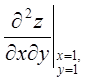
(Ⅰ)证明:对任意的正整数n,都有
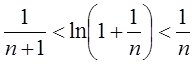
成立;
(Ⅱ)设
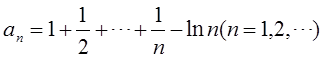
证明数列{an}收敛。
设函数y=y(x)由参数方程
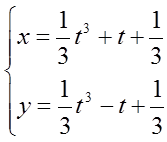
确定,求y=y(x)的极值和曲线y=y(x)的凹凸区间及拐点。
- 参考答案:
- 您的答案:
参考解析:
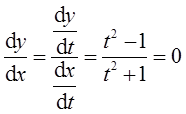
得t=±1,
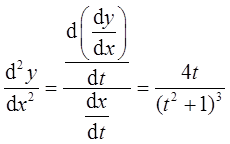
当t=-1时,因为
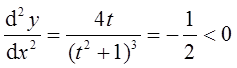
所以当t=-1即x=-1时,函数取极大值y=1。
当t=1时,因为
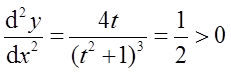
所以当t=1即x=5/3时,函数取极小值y=-1/3。
令
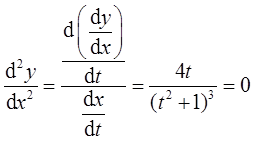
得t=0。
当t<0时,
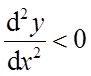
当t>0时,
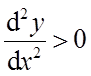
当t<0即x∈(-∞,1/3)时,函数为凸函数,故凸区间为(-∞,1/3);
当t>0即x∈(1/3,+∞)时,函数为凹函数,故凹区间为(1/3,+∞)。
当t=0时,x=1/3,y=1/3,曲线拐点为(1/3,1/3)。
设函数y(x)具有二阶导数,且曲线l:y=y(x)与直线y=x相切于原点,记α为曲线l在点(x,y)处切线的倾角,若
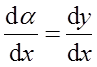
求y(x)的表达式。