曲线y=x2与曲线y=alnx(a≠0)相切,则a=( )。
- A 4e
- B 3e
- C 2e
- D e
- 参考答案:C
- 您的答案:
参考解析:

设函数z=z(x,y)由方程F(y/x,z/x)=0确定,其中F为可微函数,且F2′≠0,则x·(?z/?x)+y·(?z/?y)=( )。
- A x
- B z
- C -x
- D -z
- 参考答案:B
- 您的答案:
参考解析:
由F(y/x,z/x)=0得
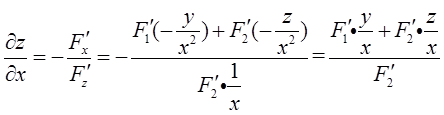
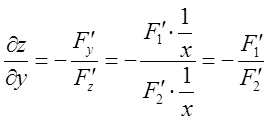
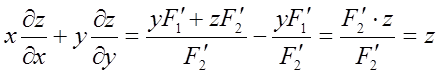
设y1,y2是一阶线性非齐次微分方程y′+p(x)y=q(x)的两个特解,若常数λ,μ使λy1+μy2是该方程的解,λy1-μy2是该方程对应的齐次方程的解,则( )。
- A λ=1/2,μ=1/2
- B λ=-1/2,μ=-1/2
- C λ=2/3,μ=1/3
- D λ=2/3,μ=2/3
- 参考答案:A
- 您的答案:
参考解析:
因λy1-μy2是y′+p(x)y=0的解,故(λy1-μy2)′+p(x)(λy1-μy2)=0。所以λ(y1′+p(x)y1)′-μ(y2′+p(x)y2)=0。而由y1′+p(x)y1=q(x),y2′+p(x)y2=q(x),所以有(λ-μ)q(x)=0。
又因λy1+μy2是非齐次y′+p(x)y=q(x)的解,故(λy1+μy2)′+p(x)(λy1+μy2)=q(x)。所以(λ+μ)q(x)=q(x)。故λ=μ=1/2。
设m,n为正整数,则反常积分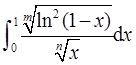 的收敛性( )。
的收敛性( )。
- A 仅与m取值有关
- B 仅与n取值有关
- C 与m,n取值都有关
- D 与m,n取值都无关
- 参考答案:D
- 您的答案:
参考解析:
分析过程如下。根据题目有
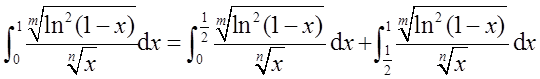
①对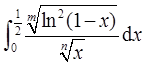 进行讨论:被积函数只在x→0+时无界。因为
进行讨论:被积函数只在x→0+时无界。因为
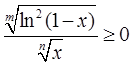
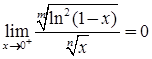
又反常积分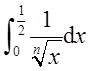 收敛,所以
收敛,所以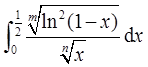 收敛。
收敛。
②对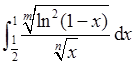 进行讨论:被积函数只在x→1-时无界。因为
进行讨论:被积函数只在x→1-时无界。因为
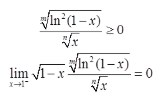
且反常积分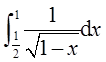 收敛,所以
收敛,所以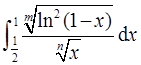 收敛。
收敛。
综上,无论正整数m和n取何值,反常积分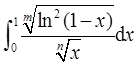 都收敛,故选D。
都收敛,故选D。
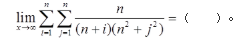
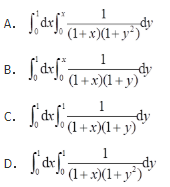
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
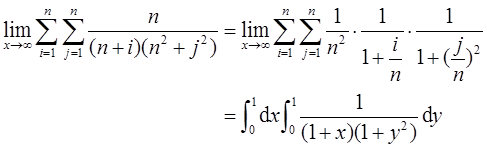
设向量组Ⅰ:α1,α2,…,αr可由向量组Ⅱ:β1,β2,…,βs线性表示,下列命题正确的是( )。
- A 若向量组Ⅰ线性无关,则r≤s
- B 若向量组Ⅰ线性相关,则r>s
- C 若向量组Ⅱ线性无关,则r≤s
- D 若向量组Ⅱ线性相关,则r>s
- 参考答案:A
- 您的答案:
参考解析:
由于向量组Ⅰ能由向量组Ⅱ线性表示,所以r(Ⅰ)≤r(Ⅱ),即r(α1,α2,…,αr)≤r(β1,β2,…,βs)≤s。若向量组Ⅰ线性无关,则r(α1,α2,…,αr)=r,所以r(α1,α2,…,αr)≤r(β1,β2,…,βs)≤s。即r≤s,选A项。
设A为4阶实对称矩阵,且A2+A=O。若A的秩为3,则A相似于( )。
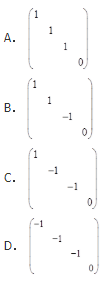
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
设λ为A的特征值,由于A2+A=O,所以λ2+λ=0,即(λ+1)λ=0。这样A的特征值为-1或0。由于A为实对称矩阵,故A可相似对角化,即A~Λ,r(A)=r(Λ)=3。
因此
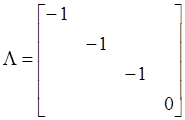
即
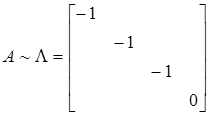
曲线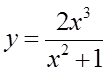
的渐近线方程为
- 参考答案:y=2x
- 您的答案:
参考解析:
3阶常系数线性齐次微分方程y?-2y″+y′-2y=0的通解y=
- 参考答案:C1e2x+C2cosx+C3sinx,其中C1,C2,C3为任意常数
- 您的答案:
参考解析:
函数y=ln(1-2x)在x=0处的n阶导数y(n)(0)=
- 参考答案:-2n·(n-1)!
- 您的答案:
参考解析:
已知一个长方形的长l以2cm/s的速率增加,宽w以3cm/s的速率增加,则当l=12cm,w=5cm时,它的对角线增加的速率为
- 参考答案:3cm/s
- 您的答案:
参考解析:
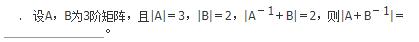
- 参考答案:3
- 您的答案:
参考解析:
求函数 的单调区间与极值.
的单调区间与极值.
- 参考答案:
- 您的答案:
参考解析:
函数f(x)的定义域(-∞,+∞),由于
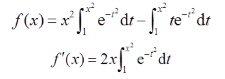
所以驻点为x=0,±1。
列表讨论如下:
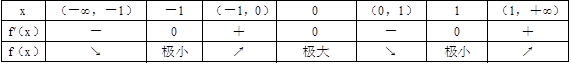
因此,f(x)的单调增区间为(-1,0)及(1,+∞),单调递减区间为(-∞,-1)及(0,1);极小值f(±1)=0,极大值
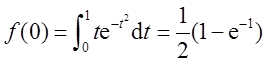
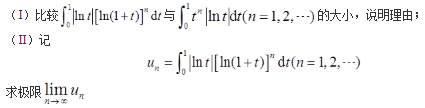
- 参考答案:
- 您的答案:
参考解析:
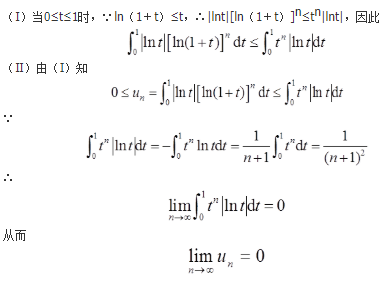
设函数y=f(x)由参数方程
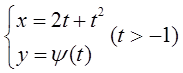
所确定,其中ψ(t)具有2阶导数,且ψ(1)=5/2,ψ′(1)=6,已知
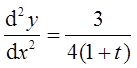
求函数ψ(t)。
- 参考答案:
- 您的答案:
参考解析:

一个高为l的柱体形贮油罐,底面是长轴为2a,短轴为2b的椭圆。现将贮油罐平放,当油罐中油面高度为3b/2时,计算油的质量。(长度单位为m,质量单位为kg,油的密度为常数ρkg/m3)
- 参考答案:
- 您的答案:
参考解析:
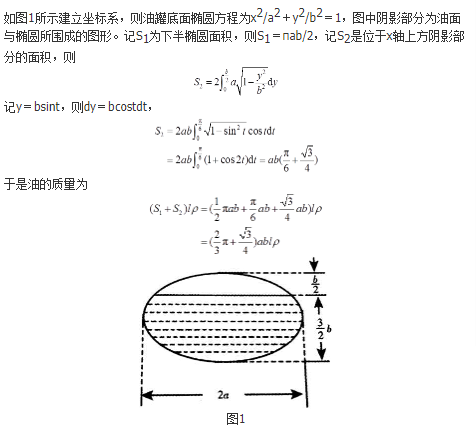

- 参考答案:
- 您的答案:
参考解析:
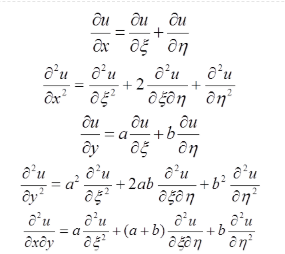
将以上各式代入原等式
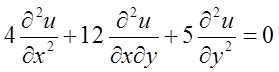
得
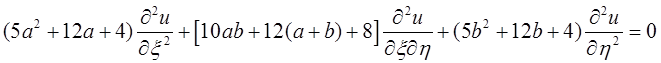
由题意,令
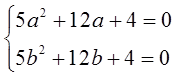
解得
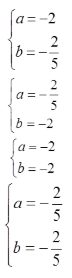
由10ab+12(a+b)+8≠0,舍去
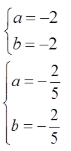
故a=-2,b=-2/5,或a=-2/5,b=-2。
计算二重积分
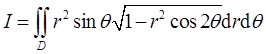
其中D={(r,θ)∣0≤r≤secθ,0≤θ≤π/4}。
- 参考答案:
- 您的答案:
参考解析:
由题设可知
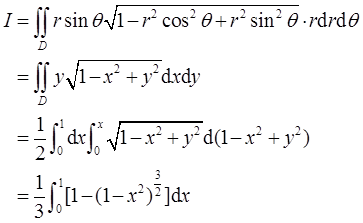
令x=sint,则dx=costdt,0<t<π/2,进一步可得

设函数f(x)在闭区间[0,1]上连续,在开区间(0,1)内可导,且f(0)=0,f(1)=1/3,证明:存在ξ∈(0,1/2),η∈(1/2,1),使得f′(ξ)+f′(η)=ξ2+η2。
- 参考答案:
- 您的答案:
参考解析:
证明:设函数F(x)=f(x)-x3/3,由题意知F(0)=0,F(1)=0。
在[0,1/2]和[1/2,1]上分别应用拉格朗日中值定理,有
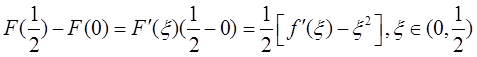
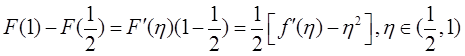
二式相加得:
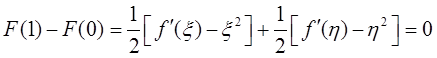
即f′(ξ)+f′(η)=ξ2+η2。
设
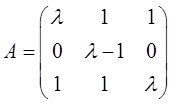
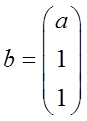
已知线性方程组Ax=b存在2个不同的解。
(Ⅰ)求λ、a;
(Ⅱ)求方程组Ax=b的通解。
- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)设η1,η2为Ax=b的2个不同的解,则η1-η2是Ax=0的一个非零解,故|A|=(λ-1)2(λ+1)=0,于是λ=1或λ=-1。
当λ=1时,因为r(A)≠r(A,b),所以Ax=b无解,舍去。
当λ=-1时,对Ax=b的增广矩阵施以初等变换,有
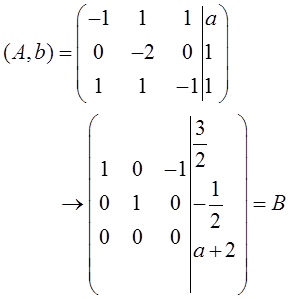
∵Ax=b有解,∴a=-2。
(Ⅱ)当λ=-1,a=-2时,
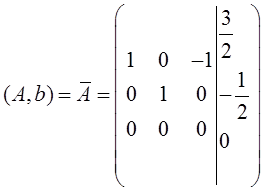
所以Ax=b的通解为
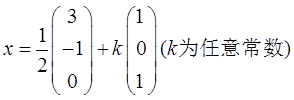
设
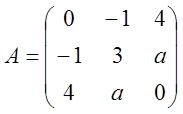
正交矩阵Q使得QTAQ为对角矩阵,若Q的第一列为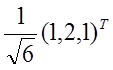 ,求a、Q。
,求a、Q。
- 参考答案:
- 您的答案:
参考解析:

