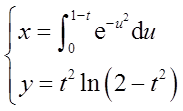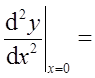设函数z=f(x,y)的全微分为dz=xdx+ydy,则点(0,0)( )。
- A 不是f(x,y)的连续点
- B 不是f(x,y)的极值点
- C 是f(x,y)的极大值点
- D 是f(x,y)的极小值点
- 参考答案:D
- 您的答案:
参考解析:
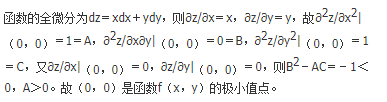
若f″(x)不变号,且曲线y=f(x)在点(1,1)上的曲率圆为x2+y2=2,则函数f(x)在区间(1,2)内( )。
- A 有极值点,无零点
- B 无极值点,有零点
- C 有极值点,有零点
- D 无极值点,无零点
- 参考答案:B
- 您的答案:
参考解析:
由题意可知,f(x)是一个凸函数,即f″(x)<0,且在点(1,1)处的曲率
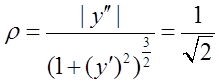
而f′(1)=-1,由此可得,f″(1)=-2。在[1,2]上,f′(x)≤f′(1)=-1<0,即f(x)单调减少,没有极值点。对于f(2)-f(1)=f′(ξ)<-1,ξ∈(1,2)(拉格朗日中值定理)。
又因为f(1)=1>0,且f(2)-f(1)<-1,所以f(2)<0,由零点定理知,在[1,2]上,f(x)有零点。故应选B项。
函数
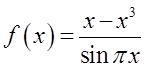
的可去间断点的个数为( )。
- A 1
- B 2
- C 3
- D 无穷多个
- 参考答案:C
- 您的答案:
参考解析:
由于
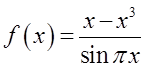
则当x取任何整数时,f(x)均无意义。
故f(x)的间断点有无穷多个,但可去间断点为极限存在的点,故应是x-x3=0的解x1,2,3=0,±1。而
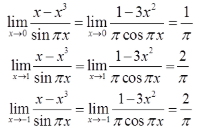
故可去间断点为3个,即0,±1。
当x→0时,f(x)=x-sinax与g(x)=x2ln(1-bx)是等价无穷小,则( )。
- A a=1,b=-1/6
- B a=1,b=1/6
- C a=-1,b=-1/6
- D a=-1,b=1/6
- 参考答案:A
- 您的答案:
参考解析:
当x→0时,有ln(1-x)~x,sinx~x,结合等价无穷小和洛必达法则,可得
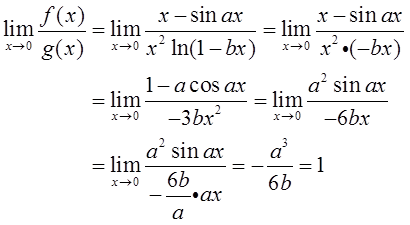
∴a3=-6b,故排除BC两项。另外,存在,蕴含了1-acosax→0(x→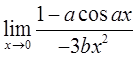 0),故a=1。排除D项。所以本题选A项。
0),故a=1。排除D项。所以本题选A项。
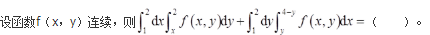
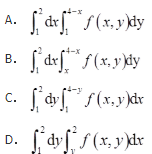
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

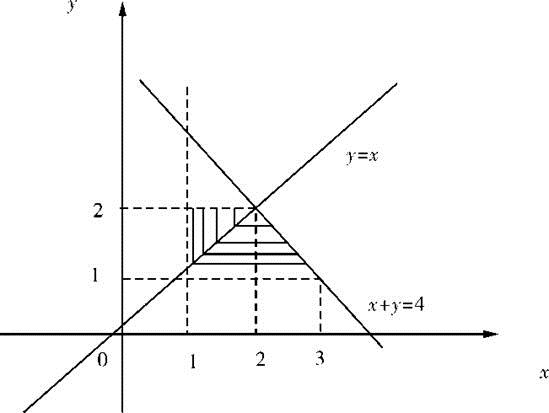
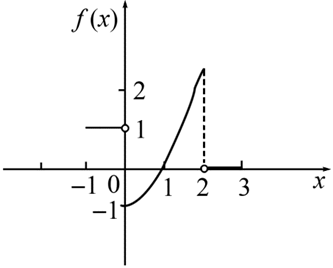
设函数y=f(x)在区间[-1,3]上的图形如图2所示。
则函数
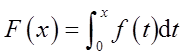
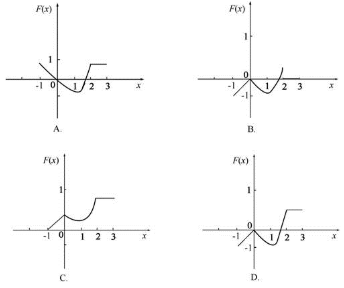
的图形为( )。
- A A
- B B
- C C
- D D
- 参考答案:D
- 您的答案:
参考解析:
由y=f(x)的图形可见,其图像与x轴及y轴、x=x0所围的图形的代数面积为所求函数F(x),从而可得出几个方面的特征:①x∈[0,1]时,F(x)≤0,且单调递减;②x∈[1,2]时,F(x)单调递增;③x∈[2,3]时,F(x)为常函数;④x∈[-1,0]时,F(x)≤0为线性函数,单调递增;⑤F(x)为连续函数。结合这些特点,可见D项正确。
设A,B均为2阶矩阵,A*,B*分别为A,B的伴随矩阵,若|A|=2,|B|=3,则分块矩阵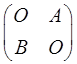 的伴随矩阵为( )。
的伴随矩阵为( )。
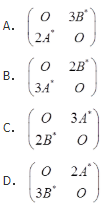
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
分块矩阵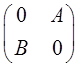 的行列式
的行列式
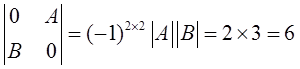
即分块矩阵可逆。
根据CC*=|C|E,C*=|C|C-1,C-1=C*/|C|,可得
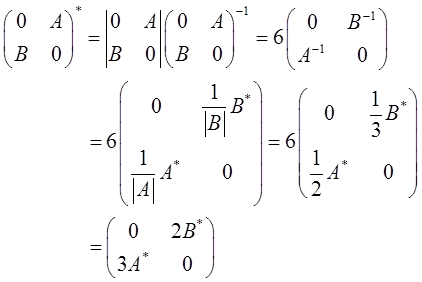
设A,P均为3阶矩阵,PT为P的转置矩阵,且
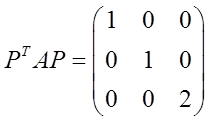
若P=(α1,α2,α3),Q=(α1+α2,α2,α3),则QTAQ为( )。
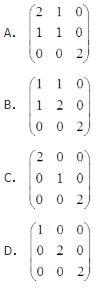
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
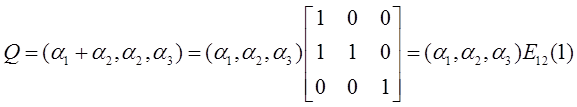
即Q=PE12(1),则
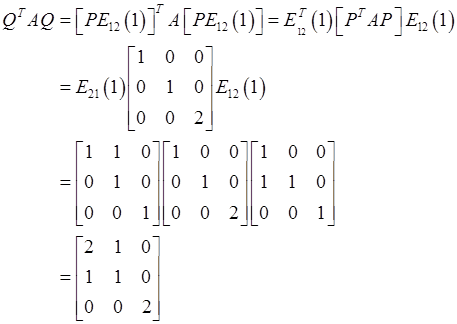
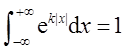 ,则k=
,则k=