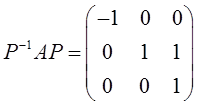设函数f(x)在(-∞,+∞)内单调有界,{xn}为数列,下列命题正确的是( )。
- A 若{xn}收敛,则{f(xn)}收敛
- B 若{xn}单调,则{f(xn)}收敛
- C 若{f(xn)}收敛,则{xn}收敛
- D 若{f(xn)}单调,则{xn}收敛
- 参考答案:B
- 您的答案:
参考解析:
由题意知,若{xn}单调,则{f(xn)}单调有界,则{f(xn)}一定存在极限,即{f(xn)}收敛。
设f(x)=x2(x-1)(x-2),则f′(x)的零点个数为( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:D
- 您的答案:
参考解析:
f′(x)=4x3+3x2-4x=x(4x2+3x-4)。令f′(x)=0,可得f′(x)有三个零点。
如图1所示,曲线方程为y=f(x),函数在区间[0,a]上有连续导数,则定积分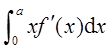 在几何上表示( )。
在几何上表示( )。
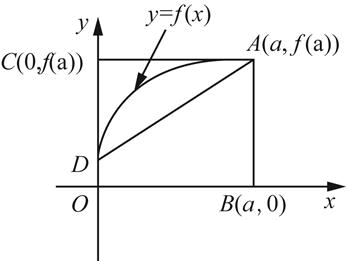
- A 曲边梯形ABOD面积
- B 梯形ABOD的面积
- C 曲边三角形ACD面积
- D 三角形ACD面积
- 参考答案:C
- 您的答案:
参考解析:
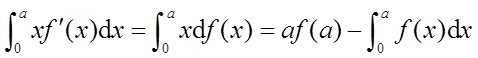
其中af(a)是矩形面积,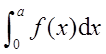 为曲边梯形的面积,所以
为曲边梯形的面积,所以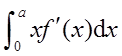 为曲边三角形ACD的面积。
为曲边三角形ACD的面积。
在下列微分方程中,以y=C1ex+C2cos2x+C3sin2x(C1,C2,C3为任意的常数)为通解的是( )。
- A y?+y″-4y′-4y=0
- B y?+y″+4y′+4y=0
- C y?-y″-4y′+4y=0
- D y?-y″+4y′-4y=0
- 参考答案:D
- 您的答案:
参考解析:
由y=C1ex+C2cos2x+C3sin2x,可知其特征根为λ1=1,λ2,3=±2i,故对应的特征值方程为
(λ-1)(λ+2i)(λ-2i)=(λ-1)(λ2+4)=λ3-λ2+4λ-4
所以所求微分方程为y?-y″+4y′-4y=0。
判定函数
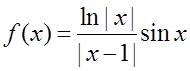
间断点的情况( )。
- A 有一个可去间断点,一个跳跃间断点
- B 有一个可去间断点,一个无穷间断点
- C 有两个跳跃间断点
- D 有两个无穷间断点
- 参考答案:A
- 您的答案:
参考解析:
函数可能的间断点有x=0,x=1两个。
在x=0时,
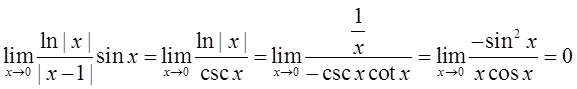
故x=0是可去间断点。
在x=1时,
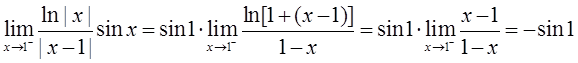
故x=1是跳跃间断点。
设函数f(x)连续,
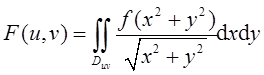
其中区域Duv如图2阴影部分所示,则?F/?u=( )。
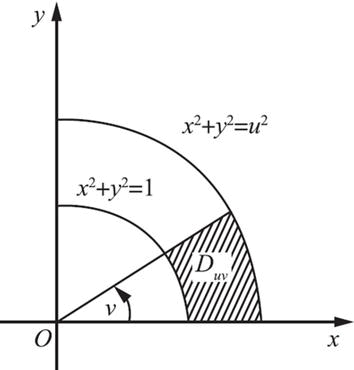
- A vf(u2)
- B vf(u)
- C vf(u2)/u
- D vf(u)/u
- 参考答案:A
- 您的答案:
参考解析:
利用极坐标,得
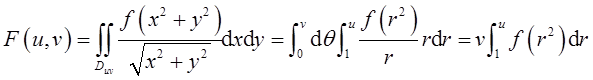
所以?F/?u=vf(u2)。
设A为n阶非零矩阵,E为n阶单位矩阵。若A3=O,则下列结论正确的是( )。
- A E-A不可逆,则E+A不可逆
- B E-A不可逆,则E+A可逆
- C E-A可逆,则E+A可逆
- D E-A可逆,则E+A不可逆
- 参考答案:C
- 您的答案:
参考解析:
(E-A)(E+A+A2)=E-A3=E,(E+A)(E-A+A2)=E+A3=E。故E-A,E+A均可逆。
设
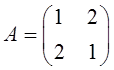
则在实数域上,与A合同的矩阵为( )。
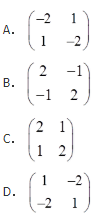
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
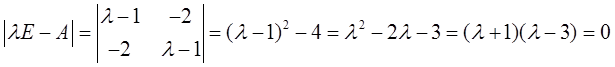
则λ1=-1,λ2=3,记
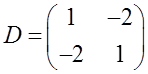
则
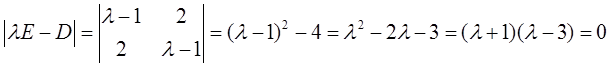
则λ1=-1,λ2=3,矩阵A和矩阵D的正负惯性指数相同,故选D项。
已知函数f(x)连续,且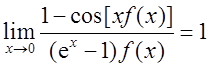
则f(0)=
。
- 参考答案:2
- 您的答案:
参考解析:
微分方程(y+x2e-x)dx-xdy=0的通解是____。
- 参考答案:y=x(C-e-x)
- 您的答案:
参考解析:
曲线sinxy+ln(y-x)=x在点(0,1)的切线方程为______。
- 参考答案:y=x+1
- 您的答案:
参考解析:
曲线y=(x-5)x2/3的拐点坐标为___。
- 参考答案:(-1,-6)
- 您的答案:
参考解析:
设3阶矩阵A的特征值为2,3,λ。若行列式|2A|=-48,则λ=____。
- 参考答案:-1
- 您的答案:
参考解析:
求极限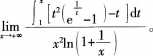
- 参考答案:
- 您的答案:
参考解析:
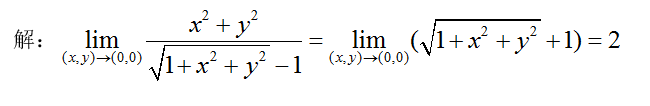
计算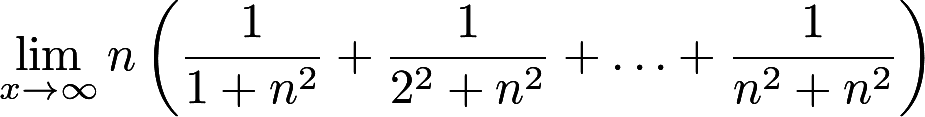
- 参考答案:
- 您的答案:
参考解析:
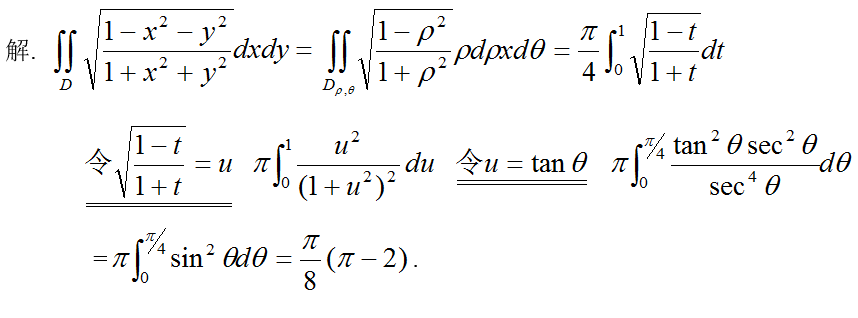
设函数y=y(x)由参数方程
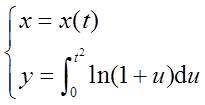
确定,其中x=x(t)是初值问题
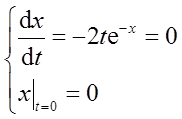
的解,求d2y/dx2。
- 参考答案:
- 您的答案:
参考解析:
由dx/dt-2te-x=0,得exdx=2tdt,积分得ex=t2+C。
由条件x|t=0=0,得C=1,即ex=t2+1,故x=ln(1+t2)。
方程组
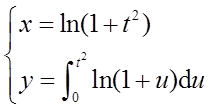
两端同时对t求导得
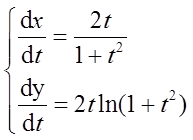
所以dy/dx=(dy/dt)/(dx/dt)=(1+t2)ln(1+t2)。
从而
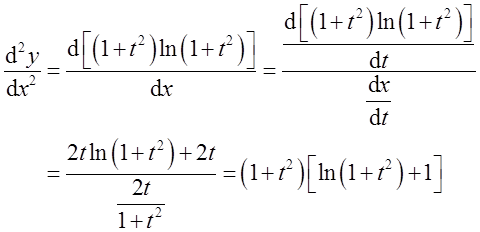
计算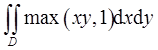 ,其中D={(x,y)|0≤x≤2,0≤y≤2}。
,其中D={(x,y)|0≤x≤2,0≤y≤2}。
- 参考答案:
- 您的答案:
参考解析:
曲线xy=1将区域D分成如图3所示的两个区域D1和D2。则有
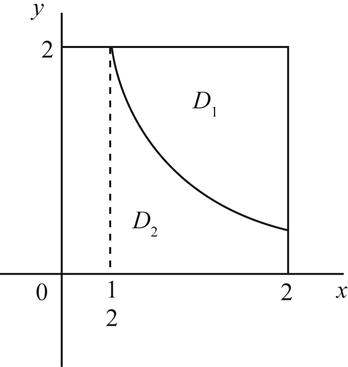
图3
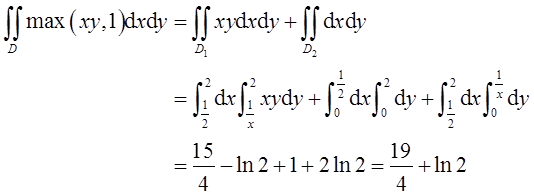
设f(x)是区间[0,+∞)上具有连续导数的单调增加函数,且f(0)=1。对任意的t∈[0,+∞),直线x=0,x=t,,曲线y=f(x)以及x轴所围成的曲边梯形绕x轴旋转一周生成一旋转体,若该旋转体的侧面面积在数值上等于其体积的2倍,求函数f(x)的表达式。
- 参考答案:
- 您的答案:
参考解析:
根据题意,因为旋转体体积
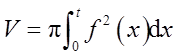
侧面积
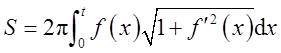
所以
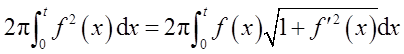
上式两边同时对t求导得
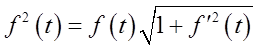
解得
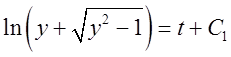
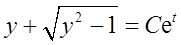
由y(0)=1,得C=1;所以
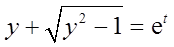
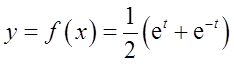
(Ⅰ)证明积分中值定理:若函数f(x)在闭区间[a,b]上连续,则至少存在一点η∈[a,b],使得
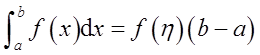
(Ⅱ)若函数φ(x)具有二阶导数,且满足φ(2)>φ(1),
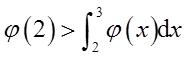
则至少存在一点ξ∈(1,3),使得φ″(ξ)<0。
- 参考答案:
- 您的答案:
参考解析:
证明:(Ⅰ)若函数f(x)在闭区间[a,b]上连续,则必存在最大值M和最小值m,即m≤f(x)≤M,x∈[a,b]。
于是有
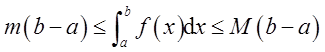
即
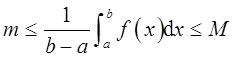
根据闭区间上连续函数的介值定理,在[a,b]上至少存在一点η∈[a,b],使得
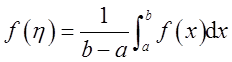
因此而得证。
(Ⅱ)根据(Ⅰ)中结论可得,存在η∈[2,3],使得
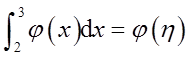
由
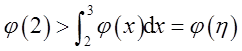
知η∈[2,3]。
由φ(2)>φ(1),利用微分中值定理,存在ξ1∈(1,2),使得
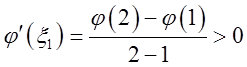
由φ(2)>φ(η),利用微分中值定理,存在ξ2∈(2,η),使得
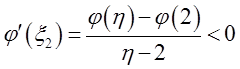
存在ξ∈(ξ1,ξ2)?(1,3),使得
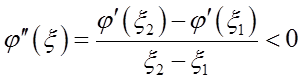
求函数u=x2+y2+z2在约束条件z=x2+y2和x+y+z=4下的最大值和最小值。
- 参考答案:
- 您的答案:
参考解析:
作拉格朗日函数
F(x,y,z)=x2+y2+z2+λ(x2+y2-z)+μ(x+y+z-4)
令
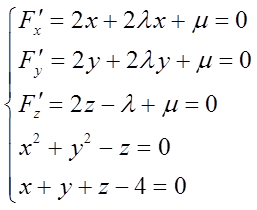
解得(x1,y1,z1)=(1,1,2),(x2,y2,z2)=(-2,-2,8)。
故所求得最大值为72,最小值为6。
设n元线性方程组Ax=b,其中
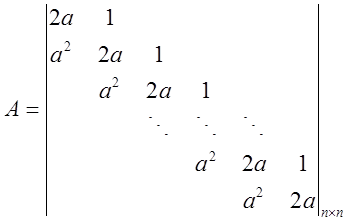
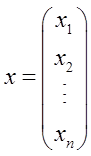
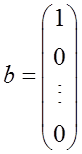
(Ⅰ)证明行列式|A|=(n+1)an;
(Ⅱ)当a为何值时,该方程组有唯一解,并求x1;
(Ⅲ)当a为何值时,该方程组有无穷多解,并求其通解。
- 参考答案:
- 您的答案:
参考解析:
证明:(Ⅰ)方法一:数学归纳法
记
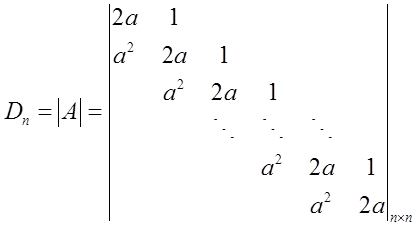
以下用数学归纳法证明Dn=(n+1)an。
当n=1时,D1=2a,结论成立;
当n=2时,
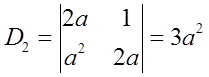
结论成立;
假设结论对小于n的情况成立。将Dn按第一行展开得
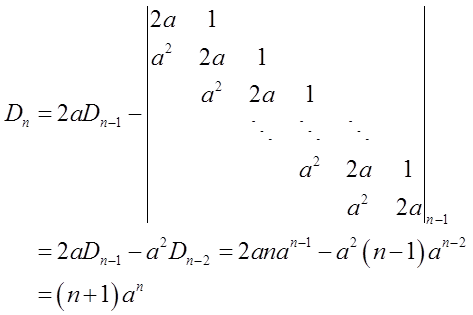
故|A|=(n+1)an。
方法二:消元法
记
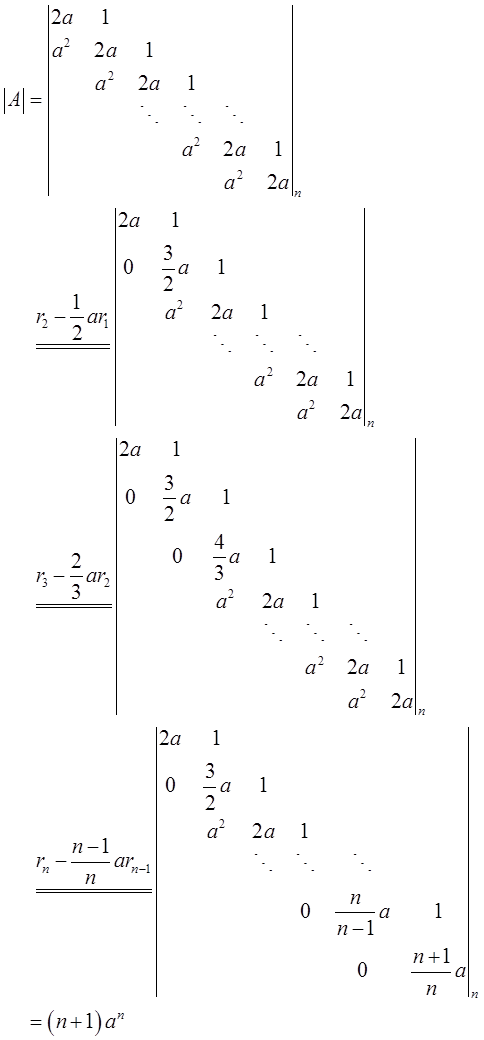
(Ⅱ)当a≠0时,方程组系数行列式Dn≠0,故方程组有唯一解。由克莱姆法则,将Dn得第一列换成b,得行列式为
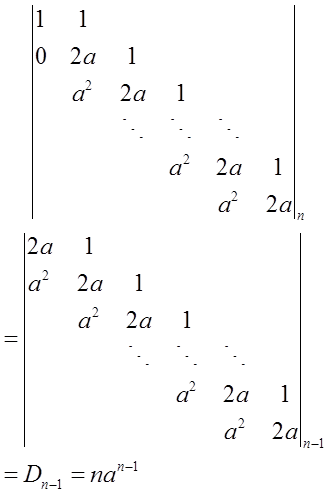
所以,当a≠0时,有唯一解
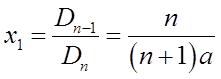
(Ⅲ)当a=0时,方程组为
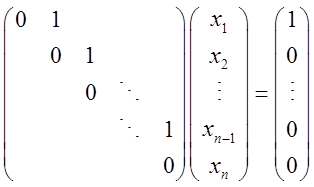
此时方程组系数矩阵得秩和增广矩阵的秩均为n-1,所以方程组有无穷多组解,其通解为x=(0,1,0,…,0)T+k(1,0,…,0)T,其中k为任意常数。
设A为3阶矩阵,α1,α2为A的分别属于-1,1的特征向量,向量α3满足Aα3=α2+α3。
(Ⅰ)证明α1,α2,α3线性无关;
(Ⅱ)令P=(α1,α2,α3),求P-1AP。
- 参考答案:
- 您的答案:
参考解析:
证明:(Ⅰ)设存在数k1,k2,k3,使得k1α1+k2α2+k3α3=0①。
由已知条件知Aα1=-α1,Aα2=α2。用矩阵A分别乘式①的左右两边,得-k1α1+k2α2+k3(α2+α3)=0②。
式①-②得2k1α1-k3α2=0。
由于α1,α2为A的分别属于-1,1的特征向量,所以α1,α2线性无关,即k1=k3=0,代入①得k2α2=0。
因为α2是A的特征向量,α2≠0,得k2=0,即k1=k2=k3=0,所以α1,α2,α3线性无关。
(Ⅱ)由题意有
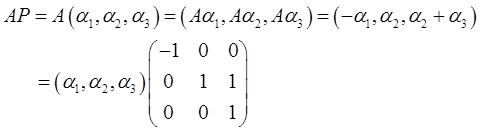
因为α1,α2,α3线性无关,所以矩阵P可逆,得