设A是4阶矩阵,A*为A的伴随矩阵,若线性方程组Ax=0的基础解系中只有2个向量,则r(A*)=( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:A
- 您的答案:
参考解析:
伴随矩阵的秩为
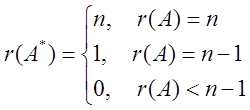
由于r(A)=n-2<n-1,所以r(A*)=0。故选A。
已知平面区域D={(x,y)∣∣x∣+∣y∣≤π/2},记
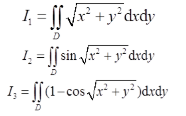
则( )。
- A I3<I2<I1
- B I2<I1<I3
- C I1<I2<I3
- D I2<I3<I1
- 参考答案:A
- 您的答案:
参考解析:

当x→0时,若x-tanx与xk是同阶无穷小,则k=( )。
- A 1
- B 2
- C 3
- D 4
- 参考答案:C
- 您的答案:
参考解析:

曲线y=xsinx+2cosx(-π/2<x<2π)的拐点是( )。
- A (0,2)
- B (π,-2)
- C (π/2,π/2)
- D (3π/2,-3π/2)
- 参考答案:B
- 您的答案:
参考解析:
由y=xsinx+2cosx计算y″得,y″=cosx-xsinx-cosx=-xsinx,令y″=0得x=0,x=π。在x=0的两侧,y″不变号,即y″(0-)y″(0+)>0,所以(0,2)不是拐点;在x=π的两侧,y″变号,即y″(π-)y″(π+)<0,所以(π,-2)是拐点。
下列反常积分发散的是( )。
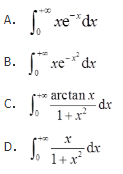
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:


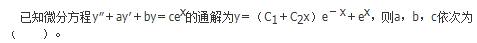
- A 1,0,1
- B 1,0,2
- C 2,1,3
- D 2,1,4
- 参考答案:D
- 您的答案:
参考解析:

设函数f(x),g(x)的2阶导函数在x=a处连续,则
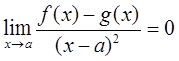
是两条曲线y=f(x),y=g(x)在x=a对应的点处相切及曲率相等的( )。
- A 充分不必要条件
- B 充分必要条件
- C 必要不充分条件
- D 既不充分也不必要条件
- 参考答案:A
- 您的答案:
参考解析:
①充分性
在x=a处,由泰勒公式得
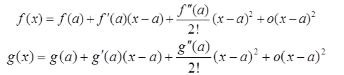
代入
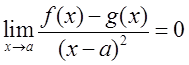
可得f(a)=g(a),f′(a)=g′(a),f″(a)=g″(a),因此两条曲线在x=a处相切且斜率相等。
②必要性
必要性不成立。例如f(x)=(x-a)2,g(x)=-(x-a)2,它们在点a相切且具有相同的曲率,但
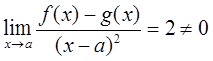
故选A。

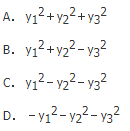
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

曲线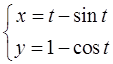
在t=3π/2对应点处的切线在y轴上的截距为
- 参考答案:3π/2+2
- 您的答案:
参考解析:
曲线y=lncosx(0≤x≤π/6)的弧长为
- 参考答案:(ln3)/2
- 您的答案:
参考解析:
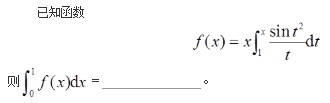
- 参考答案:(cos1-1)/4
- 您的答案:
参考解析:
已知矩阵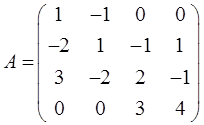
Aij表示|A|中(i,j)元的代数余子式,则A11-A12=
- 参考答案:-4
- 您的答案:
参考解析:
求不定积分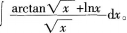
- 参考答案:
- 您的答案:
参考解析:
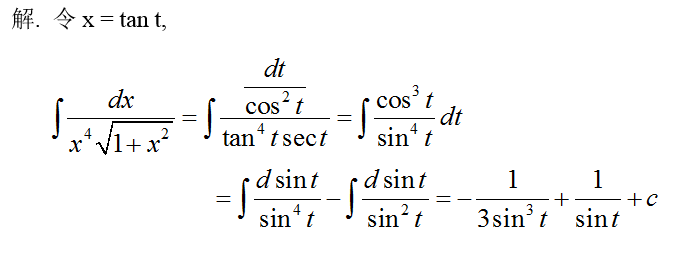
已知函数
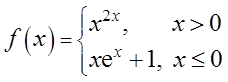
求f′(x),并求f(x)的极值。
- 参考答案:
- 您的答案:
参考解析:

设函数y(x)是微分方程
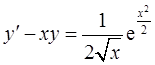
满足条件
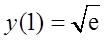
的特解。
(Ⅰ)求y(x);
(Ⅱ)设平面区域D={(x,y)|1≤x≤2,0≤y≤y(x)},求D绕x轴旋转所得旋转体的体积。
- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)用一阶线性微分方程通解公式,可得
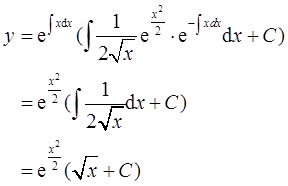
由

得C=0,所以

(Ⅱ)结合(Ⅰ)中求出的函数y(x),且D={(x,y)|1≤x≤2,0≤y≤y(x)},可得旋转体体积为

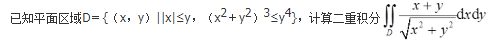
- 参考答案:
- 您的答案:
参考解析:

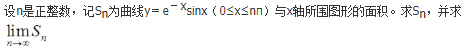
- 参考答案:
- 您的答案:
参考解析:

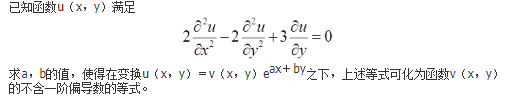
- 参考答案:
- 您的答案:
参考解析:

已知函数f(x)在[0,1]上具有2阶导数,且f(0)=0,f(1)=1,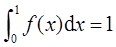 ,证明:
,证明:
(Ⅰ)存在ξ∈(0,1),使得f′(ξ)=0;
(Ⅱ)存在η∈(0,1),使得f″(η)<-2。
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:



- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)相似的矩阵有相同的特征值,因此特征值之和相同,又因为矩阵特征值之和等于矩阵的迹(矩阵对角线元素之和),所以有Σaii=Σbii,|A|=|B|,即
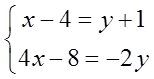
求解得到x=3,y=-2。
(Ⅱ)矩阵B的特征多项式f(λ)=|λE-B|=(λ-2)(λ+1)(λ+2),因此B的特征值为2,-1,-2。A与B相似,因此A的特征值也为2,-1,-2。
下面分别求A和B的特征向量:


