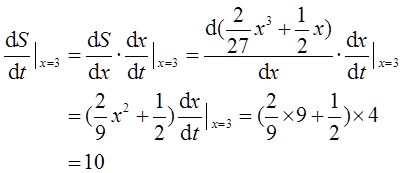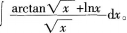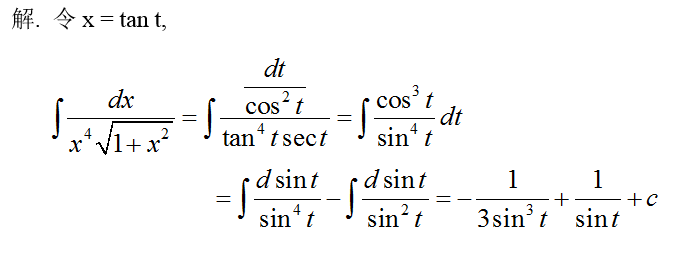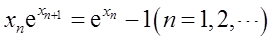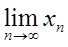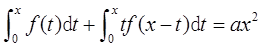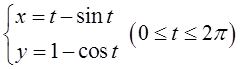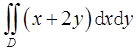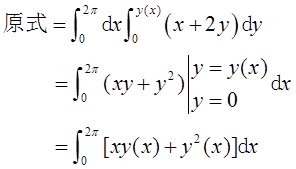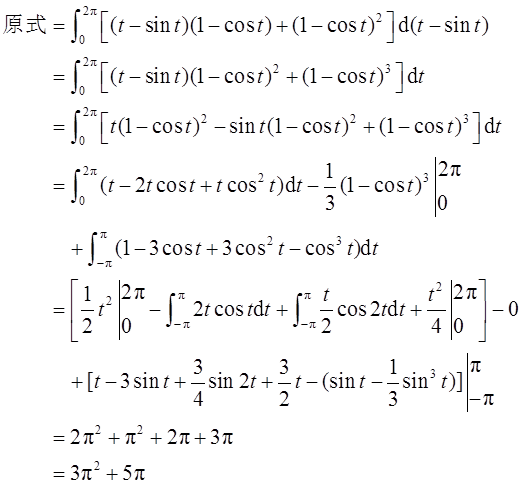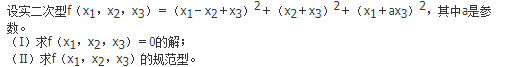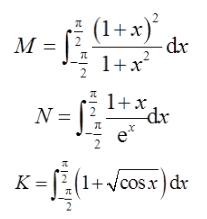 则( )。
则( )。
- A M>N>K
- B M>K>N
- C K>M>N
- D K>N>M
- 参考答案:C
- 您的答案:
参考解析:

下列函数中,在x=0处不可导的是( )。
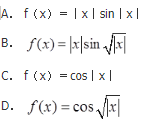
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
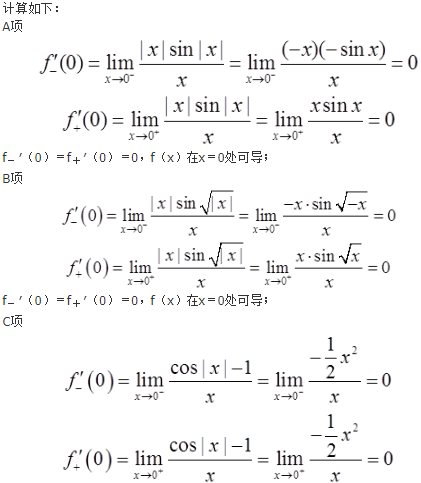

设函数f(x)在[0,1]上二阶可导,且
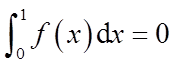
则( )。
- A 当f′(x)<0时,f(1/2)<0
- B 当f″(x)<0时,f(1/2)<0
- C 当f′(x)>0时,f(1/2)<0
- D 当f″(x)>0时,f(1/2)<0
- 参考答案:D
- 您的答案:
参考解析:


设A、B为n阶矩阵,记r(X)为矩阵X的秩,(X,Y)表示分块矩阵,则( )。
- A r(A,AB)=r(A)
- B r(A,BA)=r(A)
- C r(A,B)=max{r(A),r(B)}
- D r(A,B)=r(A^T,B^T)
- 参考答案:A
- 您的答案:
参考解析:
令AB=C,分块列阵为
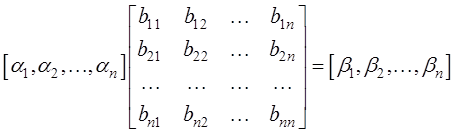
即β1,β2,…,βn,可由α1,α2,…,αn线性表出,矩阵的秩就是列向量组的秩。故r(A,AB)=r(α1,α2,…,αn,β1,β2,…,βn)=r(α1,α2,…,αn)=r(A)。
设函数
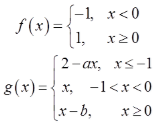
若f(x)+g(x)在R上连续,则( )。
- A a=3,b=1
- B a=3,b=2
- C a=-3,b=1
- D a=-3,b=2
- 参考答案:D
- 您的答案:
参考解析:
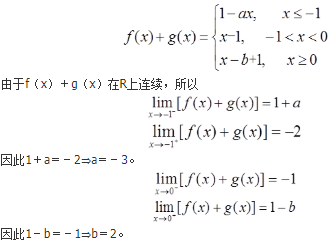
若
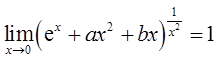
则( )。
- A a=1/2,b=?1
- B a=-1/2,b=?1
- C a=1/2,b=1
- D a=-1/2,b=1
- 参考答案:B
- 您的答案:
参考解析:
方法一:由重要极限可得
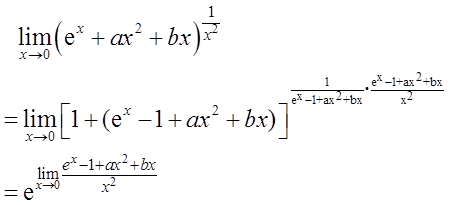

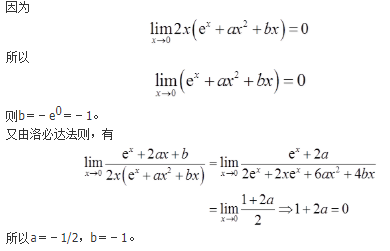
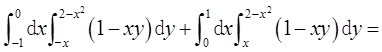
- A 5/3
- B 5/6
- C 7/3
- D 7/6
- 参考答案:C
- 您的答案:
参考解析:
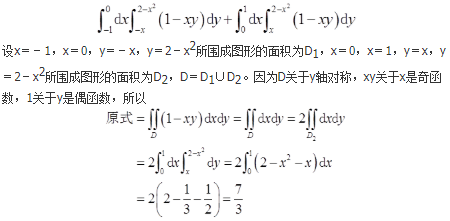

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
题设矩阵记为X,4个选项矩阵分别记为A、B、C、D,则矩阵X、A、B、C、D的三重特征值为1。
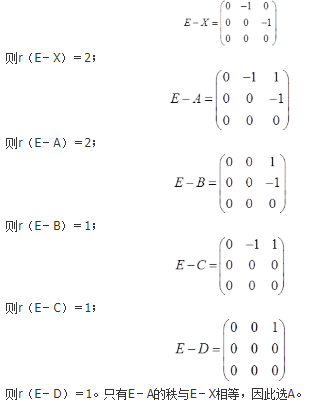
设A为3阶矩阵,α1,α2,α3为线性无关的向量组。若Aα1=2α1+α2+α3,Aα2=α2+2α3,Aα3=-α2+α3,则A的实特征值为
将长为2m的钢丝分为三段,依次围成成圆、正方形和正三角形,三个图形的面积之和是否存在最小值若存在,求出最小值。
- 参考答案:
- 您的答案:
参考解析:
设圆的半径为x,正方形边长为y,正三角形边长为z,则有2πx+4y+3z=2,其中x≥0,y≥0,z≥0。三个图形面积之和为
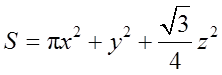
利用拉格朗日数乘法,建拉格朗日函数
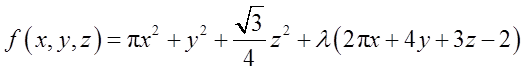
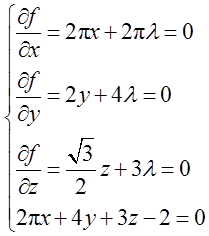
求解上述方程得到,驻点为
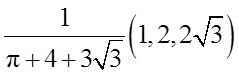
此时三个图形总面积最小,最小面积为
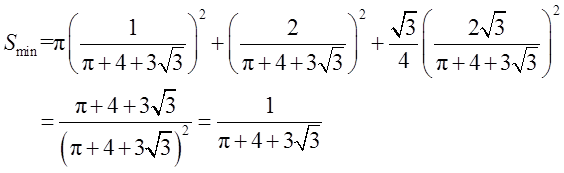
已知曲线L:y=4x2/9(x≥0),点O(0,0),点A(0,1),设P是L上的动点,S是直线OA与直线AP及曲线L所围成图形的面积,若P运动到点(3,4)时沿x轴正向的速度是4,求此时S关于时间t的变化率。
- 参考答案:
- 您的答案:
参考解析:
设点P(x,y),为使S不恒为0,则直线OA与AP不能共线,即x≠0,此时直线AP的方程为:Y=(4x/9-1/x)X+1(x≠0)。
设S所成面积为区域D,D={(X,Y)|4X2/9≤Y≤(4x/9-1/x)X+1,0≤X≤x},则

当x=3时,
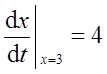
因此