已知函数f(x,y)=ex/(x-y),则( )。
- A fx′-fy′=0
- B fx′+fy′=0
- C fx′-fy′=f
- D fx′+fy′=f
- 参考答案:D
- 您的答案:
参考解析:
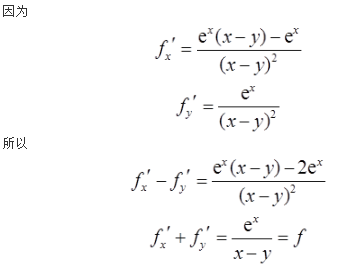
设A,B是可逆矩阵,且A与B相似,,则下列结论错误的是( )。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

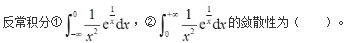
- A ①收敛,②收敛
- B ①收敛,②发散
- C ①发散,②收敛
- D ①发散,②发散
- 参考答案:B
- 您的答案:
参考解析:

设函数fi(x)(i=1,2)具有二阶连续导数,且fi″(x0)<0(i=1,2),若两条曲线y=fi(x)(i=1,2)在点(x0,y0)处具有公切线y=g(x),且在该点处曲线y=f1(x)的曲率大于曲线y=f2(x)的曲率,则在x0的某个邻域内,有( )。
- A f1(x)≤f2(x)≤g(x)
- B f2(x)≤f1(x)≤g(x)
- C f1(x)≤g(x)≤f2(x)
- D f2(x)≤g(x)≤f1(x)
- 参考答案:A
- 您的答案:
参考解析:
由题可知,f1(x0)=f2(x0)=g(x0),f1′(x0)=f2′(x0)=g′(x0),且根据曲率大小关系有f1″(x0)<f2″(x0),g″(x0)=0。
令F(x)=f1(x)-f2(x),则F(x0)=0,F′(x0)=f1′(x0)-f2′(x0)=0,F″(x0)=f1″(x0)-f1″(x0)<0。所以,F(x0)=0为F(x)的一个极大值,即在x0的某个邻域内F(x)≤0,也即f1(x)≤f2(x)。
同理设G(x)=fi(x)-g(x)(i=1,2),可得在x0的某个邻域内G(x)≤0,也即fi(x)≤g(x)。
综上,在x0的某个邻域内,f1(x)≤f2(x)≤g(x)。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
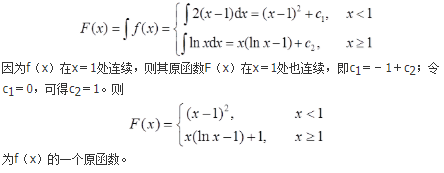
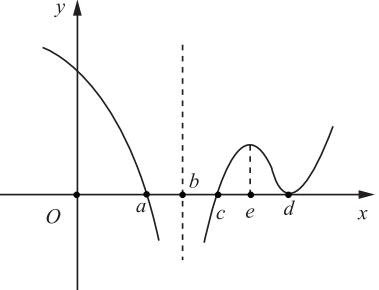
设函数f(x)在(-∞,+∞)内连续,其导函数的图形如图1所示,则( )。
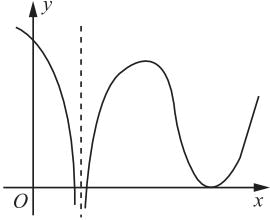
- A 函数f(x)有2个极值点,曲线y=f(x)有2个拐点
- B 函数f(x)有2个极值点,曲线y=f(x)有3个拐点
- C 函数f(x)有3个极值点,曲线y=f(x)有1个拐点
- D 函数f(x)有3个极值点,曲线y=f(x)有2个拐点
- 参考答案:B
- 您的答案:
参考解析:
如图2所示,f′(x)在a,c,d三点取值为0,有可能为f(x)的极值点。a点:当x<a时,f′(x)>0;当x>a时,f′(x)<0,所以a点为极大值点。c点:当x<c时,f′(x)<0;当x>c时,f′(x)>0,所以c点为极小值点。d点:当x<d时,f′(x)>0;当x>d时,f′(x)>0,所以d点不是极值点。所以f(x)有2个极值点。
图中,b,e,d有可能为f(x)的拐点。b点:当x<b时,f′(x)递减,f″(x)<0;当b<x<e时,f′(x)递增,f″(x)>0所以b点为拐点。e点:当b<x<e时,f′(x)递增,f″(x)>0;当e<x<d时,f′(x)递减,f″(x)<0,所以e点为拐点。d点:当e<x<d时,f′(x)递减,f″(x)<0,当x>d时,f′(x)递增,f″(x)>0,所以d点为拐点。所以f(x)有3个拐点。
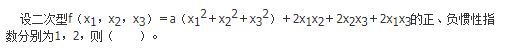
- A a>1
- B a<-2
- C -2<a<1
- D a=1或a=-2
- 参考答案:C
- 您的答案:
参考解析:

曲线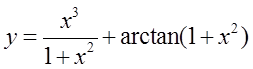
的斜渐近线方程为
- 参考答案:y=x+π/2
- 您的答案:
参考解析:
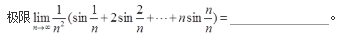
- 参考答案:sin1-cos1
- 您的答案:
参考解析:
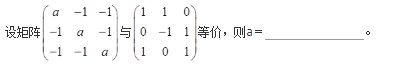
- 参考答案:2
- 您的答案:
参考解析:
设函数
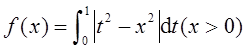
求f′(x)并求f(x)的最小值。
- 参考答案:
- 您的答案:
参考解析:
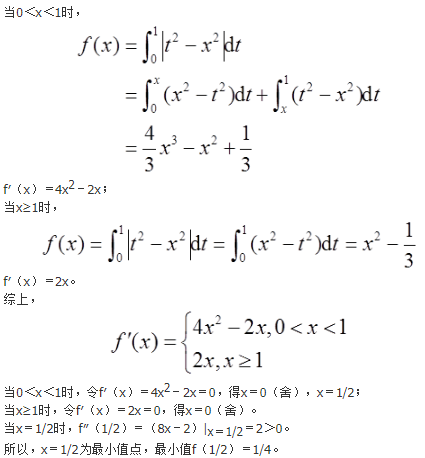
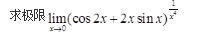
- 参考答案:
- 您的答案:
参考解析:
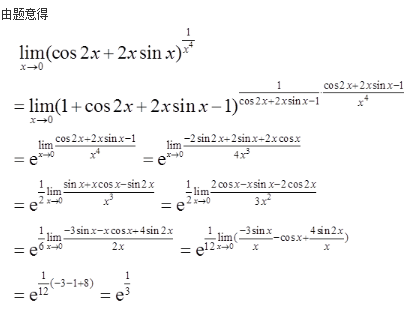
已知函数z=z(x,y)由方程(x2+y2)z+lnz+2(x+y+1)=0确定,求z=z(x,y)的极值。
- 参考答案:
- 您的答案:
参考解析:


设D是由直线y=1,y=x,y=-x围成的有界区域,计算二重积分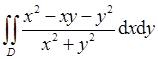
- 参考答案:
- 您的答案:
参考解析:
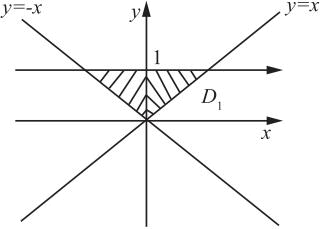
由题可画出积分区域D,如图3中阴影部分所示,可见D关于y轴对称。
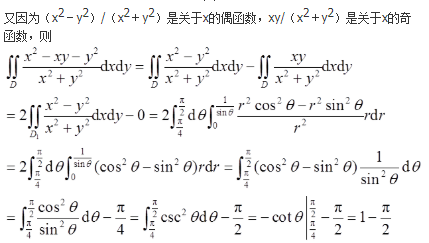

- 参考答案:
- 您的答案:
参考解析:
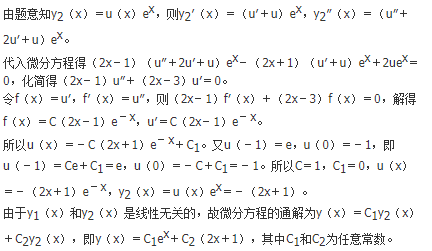
设D是由曲线
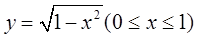
与
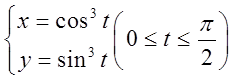
围成的平面区域,求D绕x轴旋转一周所得旋转体的体积和表面积。
- 参考答案:
- 您的答案:
参考解析:
由题可画出D如图4所示。
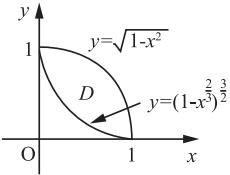
图4
则D绕x轴旋转一周所得旋转体的体积为
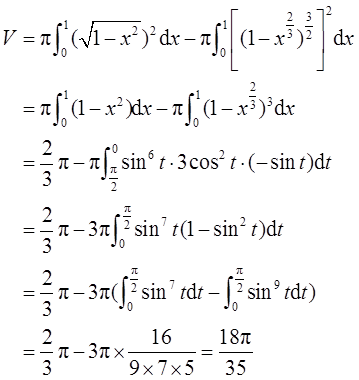
又因
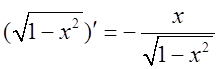
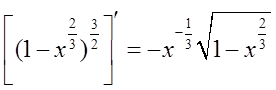
则D绕x轴旋转一周所得旋转体的表面积为
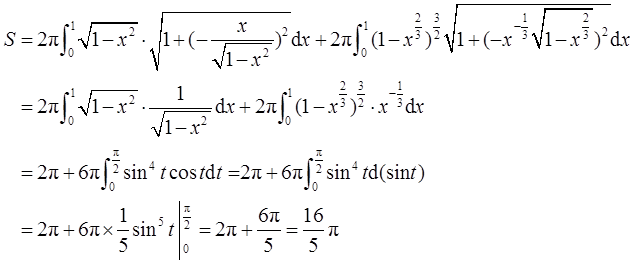
已知f(x)在[0,3π/2]上连续,在(0,3π/2)内是函数cosx/(2x-3π)的一个原函数f(0)=0。
(Ⅰ)求f(x)在区间[0,3π/2]上的平均值;
(Ⅱ)证明f(x)在区间(0,3π/2)内存在唯一零点。
- 参考答案:
- 您的答案:
参考解析:

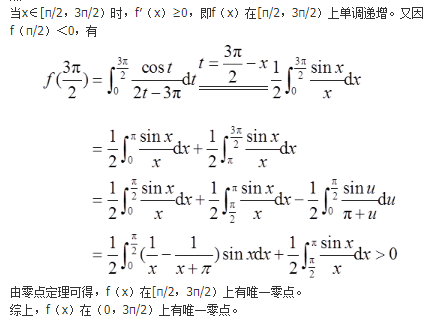

- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)方程组Ax=β无解,于是有r(A)<r(A,β)≤3,所以|A|=0,则
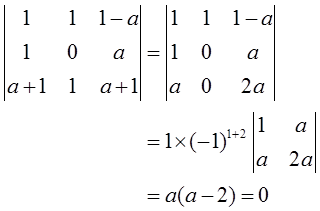
所以a=0或a=2。
当a=0时,有
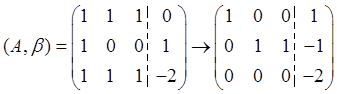
可得r(A)≠r(A,β),此时Ax=β无解。
当a=2时,有
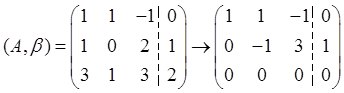
可得r(A)=r(A,β)=2<3,此时Ax=β有解,故a≠2。
综上,a=0。
(Ⅱ)由(Ⅰ)可知a=0,则


- 参考答案:
- 您的答案:
参考解析:



