下列反常积分收敛的是( )
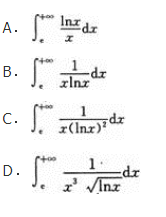
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
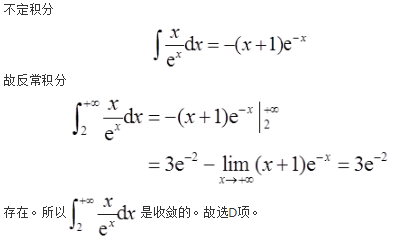
设函数
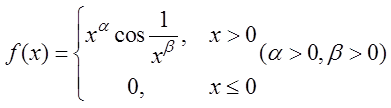
若f′(x)在x=0处连续,则( )。
- A α-β>1
- B 0<α-β≤1
- C α-β>2
- D 0<α-β≤2
- 参考答案:A
- 您的答案:
参考解析:
当x<0时,f′(x)=0,f-′(0)=0。当x>0时,有
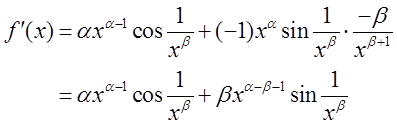
运用单侧极限的定义,有
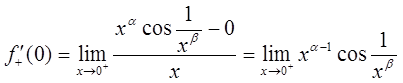
∵f′(x)在x=0处连续,∴
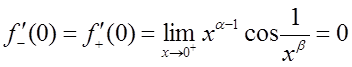
得到α-1>0。
又
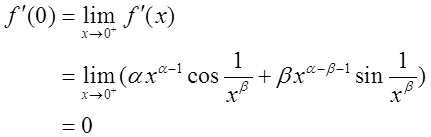
综上可得α-β-1>0,故答案选A项。
设函数f(u,v)满足f(x+y,y/x)=x2-y2,则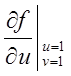 与
与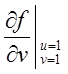 依次是( )。
依次是( )。
- A 1/2,0
- B 0,1/2
- C -1/2,0
- D 0,-1/2
- 参考答案:D
- 您的答案:
参考解析:
令u=x+y,v=y/x,则x=u/(1+v),y=uv/(1+v)。将上式代入f(x+y,y/x)=x2-y2,可以得到f(x+y,y/x)关于u,v的表达式,即
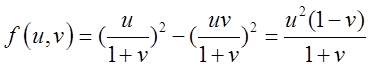
∵
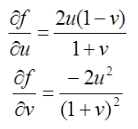
∴
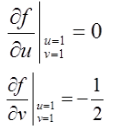
故答案选D项。
函数
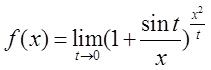
在(-∞,+∞)内( )。
- A 连续
- B 有可去间断点
- C 有跳跃间断点
- D 有无穷间断点
- 参考答案:B
- 您的答案:
参考解析:
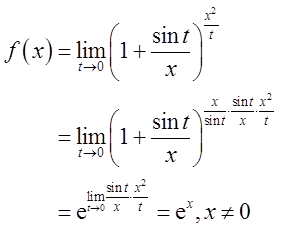
∴f(x)在x=0点左右极限都存在且f(0+)=f(0-)=1,又由于f(x)在x=0无定义,根据间断点定义及性质判断,f(x)有可去间断点x=0。故选B项。
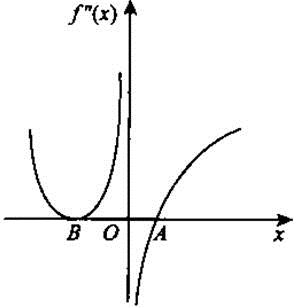
设函数f(x)在(-∞,+∞)连续,其2阶导函数f″(x)的图形如图1所示,则曲线y=f(x)的拐点个数( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:
函数f(x)在(-∞,+∞)内连续,观察图1可知,函数f(x)在除去点x=0外处处二阶可导。如图1所示,虽然f″(0)不存在,但在点x=0两侧f″(x)异号,因此(0,f(0))是y=f(x)的拐点。
A点处二阶导数为0,且A点两侧f″(x)异号,根据拐点的定义知,A点为曲线的拐点。B点处虽然二阶导数也为0,但是B点两侧f″(x)都是大于0,因此,B点不是拐点。
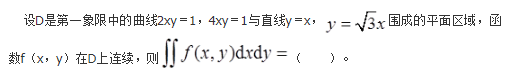
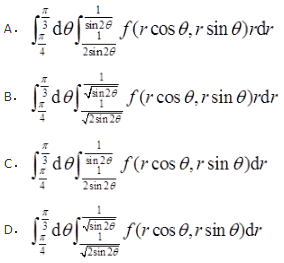
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
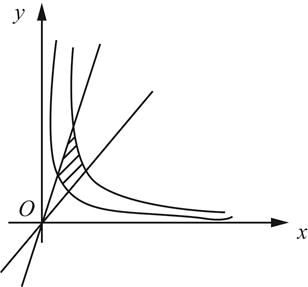
平面区域D的图形为图2中阴影部分。
作极坐标变换,令
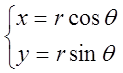
则该二重积分区域变为
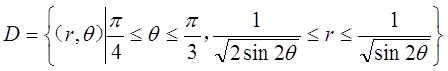
所以
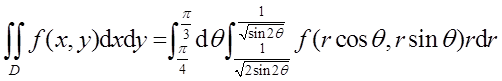
故答案选B项。
设矩阵
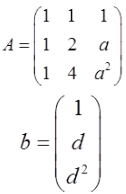
若集合Ω={1,2},则线性方程Ax=b有无穷多个解的充分必要条件为( )。
- A a?Ω,d?Ω
- B a?Ω,d∈Ω
- C a∈Ω,d?Ω
- D a∈Ω,d∈Ω
- 参考答案:D
- 您的答案:
参考解析:
Ax=b的增广矩阵,即
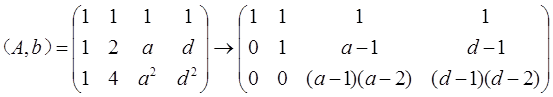
∵线性方程Ax=b有无穷多个解的充要条件是r(A)=r(A,b)<3。∴a=1或a=2同时d=1或d=2。故答案选D项。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

设函数f(x)连续,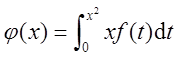
若φ(1)=1,φ′(1)=5,则f(1)=
- 参考答案:2
- 您的答案:
参考解析:

- 参考答案:n(n-1)(ln2)n-2
- 您的答案:
参考解析:
设函数y=f(x)是微分方程y″+y′-2y=0的解,且在x=0处y(x)取得极值3,则y(x)=
- 参考答案:e-2x+2ex
- 您的答案:
参考解析:
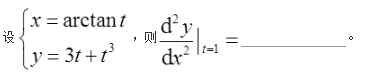
- 参考答案:48
- 您的答案:
参考解析:
设3阶矩阵A的特征值为2,-2,1,B=A2-A+E,其中E为3阶单位矩阵,则行列式|B|=
- 参考答案:21
- 您的答案:
参考解析:
已知函数
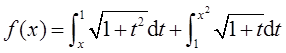
求f(x)零点的个数。
- 参考答案:
- 您的答案:
参考解析:


设函数f(x)=x+aln(1+x)+bxsinx,g(x)=kx3,若f(x)与g(x)在x→0是等价无穷小,求a,b,k的值。
- 参考答案:
- 您的答案:
参考解析:


设A>0,D是由曲线段y=Asinx(0≤x≤π/2)及直线y=0,x=π/2所围成的平面区域,V1,V2分别是D绕x轴与y轴旋转所成旋转体的体积,若V1=V2,求A的值。
- 参考答案:
- 您的答案:
参考解析:
由旋转体的体积公式,得(下式中的f(x)即为y)
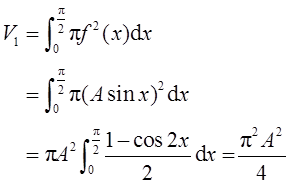
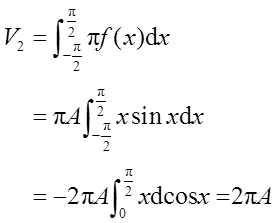
由V1=V2求得A=8/π。
已知函数f(x,y)满足fxy″=2(y+1)ex,fx′(x,0)=(x+1)ex,f(0,y)=y2+2y,求f(x,y)的极值。
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:

已知高温物体置于低温介质中,任一时刻物体温度对时间的变化率与该时刻物体和介质的温差成正比,现将一初始温度为120℃的物体在20℃的恒温介质中冷却,30min后,该物体温度降至30℃,若要物体的温度继续降至21℃,还需要冷却多长时间?
- 参考答案:
- 您的答案:
参考解析:
设t时刻物体的温度为x(t)(t单位:小时),比例常数为k(>0),介质温度为m,则dx/dt=k(x-m),从而x(t)=Cekt+m,x(0)=120,m=20,所以C=100。则t时刻物体温度方程为x(t)=100ekt+20。
∵x(1/2)=30,∴k=-(ln10)/30。∴当x=21时,t=60。故还需要冷却30min。
已知函数f(x)在区间[a,+∞)上具有2阶导数,f(a)=0,f′(x)>0,f″(x)>0,设b>a,曲线y=f(x)在点(b,f(b))处的切线与x轴的交点是(x0,0),证明:a<x0<b。
- 参考答案:
- 您的答案:
参考解析:

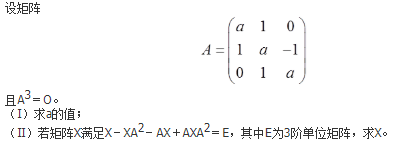
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:

