设函数
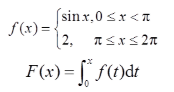
则( )。
- A x=π是函数F(x)的跳跃间断点
- B x=π是函数F(x)的可去间断点
- C F(x)在x=π处连续但不可导
- D F(x)在x=π处可导
- 参考答案:C
- 您的答案:
参考解析:
由定积分的几何意义知,F(π-0)=F(π)=F(π+0),所以F(x)在x=π处连续。而
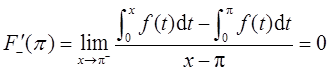
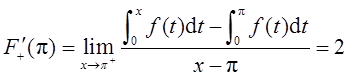
∵F-′(π)≠F+′(π),∴F(x)在x=π处不可导。故F(x)在x=π处连续但不可导。
设
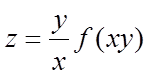
其中函数f可微,则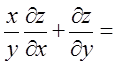 ( )。
( )。
- A 2yf′(xy)
- B -2yf′(xy)
- C 2f(xy)/x
- D -2f(xy)/x
- 参考答案:A
- 您的答案:
参考解析:
由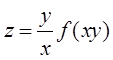 有
有
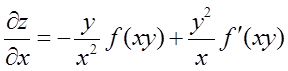
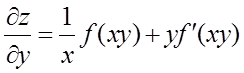
所以
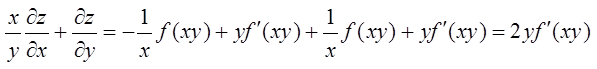
设cosx-1=xsinα(x),其中|α(x)|<π/2,则当x→0时,α(x)是( )。
- A 比x高阶的无穷小
- B 比x低阶的无穷小
- C 与x同阶但不等价的无穷小
- D 与x等价的无穷小
- 参考答案:C
- 您的答案:
参考解析:
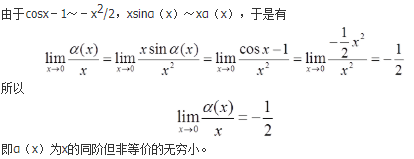
设函数y=f(x)由方程cos(xy)+lny-x=1确定,则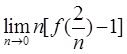 =( )。
=( )。
- A 2
- B 1
- C -1
- D -2
- 参考答案:A
- 您的答案:
参考解析:
由方程cos(xy)+lny-x=1,可解出当x=0时,y=1。在方程两端对x求导,有
{图
}∴
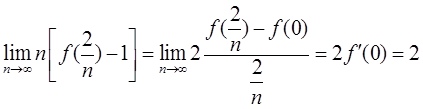
设函数
若反常积分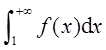 收敛,则( )。
收敛,则( )。
- A α<-2
- B α>2
- C -2<α<0
- D 0<α<2
- 参考答案:D
- 您的答案:
参考解析:
考虑积分
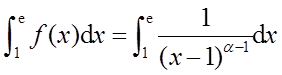
当α-1≤0,即α≤1时,为普通积分,积分自然存在;当α-1>0时,为无界函数的反常积分。且当α-1<1,即α<2时收敛,当α-1≥1,即α≥2时发散。
无穷区间上的反常积分
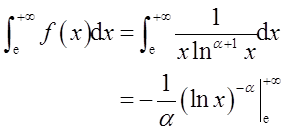
当α>0时,此反常积分收敛,α≤0时发散。由以上分析知,若反常积分收敛,则有0<α<2,因此选择D项。
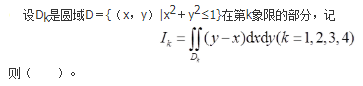
- A I1>0
- B I2>0
- C I3>0
- D I4>0
- 参考答案:B
- 您的答案:
参考解析:

设A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )。
- A 矩阵C的行向量组与矩阵A的行向量组等价
- B 矩阵C的列向量组与矩阵A的列向量组等价
- C 矩阵C的行向量组与矩阵B的行向量组等价
- D 矩阵C的列向量组与矩阵B的列向量组等价
- 参考答案:B
- 您的答案:
参考解析:
A(β1,β2,…,βn)=(γ1,γ2,…,γn),Aβi=γi(1≤i≤n),即C的列向量组可由A的列向量组线性表示。∵B可逆,∴A=CB-1,A的列向量组可由C的列向量组线性表示。矩阵C的列向量组与矩阵A的列向量组能相互线性表示,所以矩阵C的列向量组与矩阵A的列向量组等价。
矩阵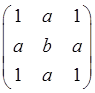 与
与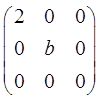 相似的充分必要条件为( )。
相似的充分必要条件为( )。
- A a=0,b=2
- B a=0,b为任意常数
- C a=2,b=0
- D a=2,b为任意常数
- 参考答案:B
- 您的答案:
参考解析:
由于A和B相似,则A和B的特征值相同。∴A和B的特征值为λ1=0,λ2=b,λ3=2。∴
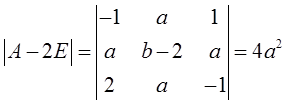
∴a=0。且R(A)=R(B),
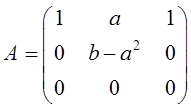
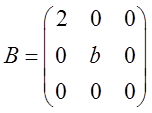
当a=0,b为任意常数时,有R(A)=R(B)。反之当b为任意常数,a=0时,有A和B相似。
设A=(aij)是3阶非零矩阵,|A|为A的行列式,Aij为aij的代数余子式,若aij+Aij=0(i,j=1,2,3),则|A|=
- 参考答案:-1
- 您的答案:
参考解析:
设封闭曲线L的极坐标方程为r=cos3θ(-π/6≤θ≤π/6),则L所围平面图形的面积是
- 参考答案:π/12
- 您的答案:
参考解析:
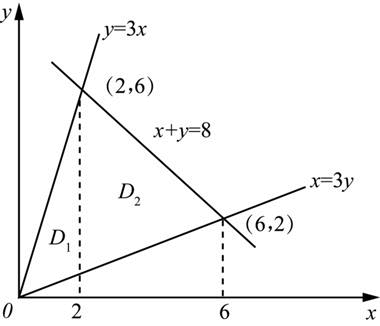
设平面内区域D由直线x=3y,y=3x及x+y=8围成,计算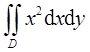
- 参考答案:
- 您的答案:
参考解析:
直线x+y=8与直线y=3x和x=3y分别交于点(2,6)和(6,2),直线x=2将区域D分为D1和D2两部分(如图1所示),则有
说明:说明:13-1
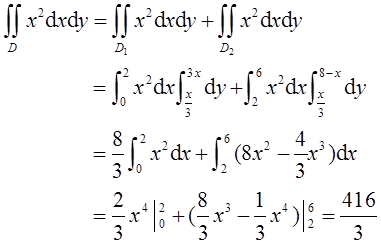
设
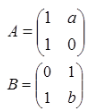
当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。
- 参考答案:
- 您的答案:
参考解析:


当x→0时,1-cosx·cos2x·cos3x与axn为等价无穷小,求n与a的值。
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:
设奇函数f(x)在[-1,1]上具有二阶导数,且f(1)=1,证明:
(Ⅰ)存在ξ∈(0,1),使得f′(ξ)=1;
(Ⅱ)存在η∈(-1,1),使得f″(η)+f′(η)=1。
- 参考答案:
- 您的答案:
参考解析:
证明:(Ⅰ)∵f(x)为奇函数,∴f(-x)=-f(x),于是f(0)=0。
令φ(x)=f(x)-x,运用罗尔中值定理,∵φ(0)=0,φ(1)=0,φ(0)=φ(1),∴?ξ∈(0,1)使φ′(ξ)=0。而φ′(x)=f′(x)-1,∴f′(ξ)=1。
(Ⅱ)∵f(x)为奇函数,∴f(-x)=-f(x),?-f′(x)=-f′(x),即f′(x)为偶函数。
又∵f′(x)为偶函数,∴f′(-ξ)=1。
令h(x)=ex[f′(x)-1]。∵h(-ξ)=h(ξ)=0,∴?η∈(-ξ,ξ)?(-1,1),使h′(η)=0。而h′(x)=ex[f′(x)-1]+exf″(x)=ex[f′(x)+f″(x)-1],且ex≠0。∴f″(η)+f′(η)=1。
求曲线x3-xy+y3=1(x≥0,y≥0)上的点到坐标原点的最长距离与最短距离。
- 参考答案:
- 您的答案:
参考解析:

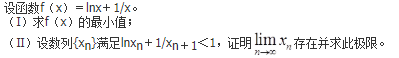
- 参考答案:
- 您的答案:
参考解析:
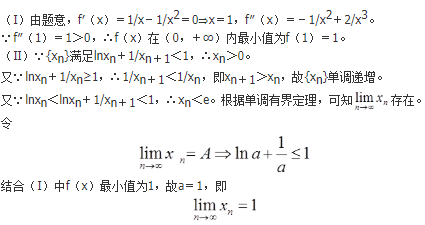
设曲线L的方程为y=x2/4-lnx/2(1≤x≤e)。
(Ⅰ)求L的弧长;
(Ⅱ)设D是由曲线L,直线x=1,x=e及x轴所围平面图形,求D的形心的横坐标。
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:

