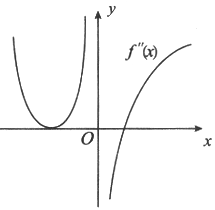
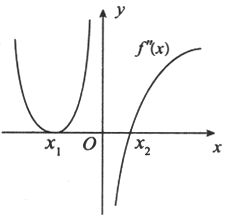
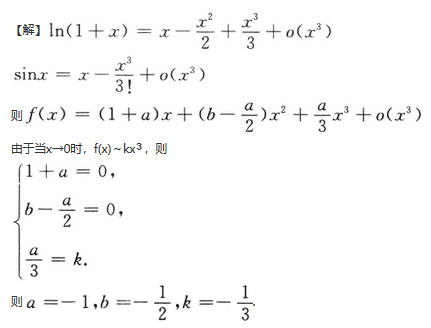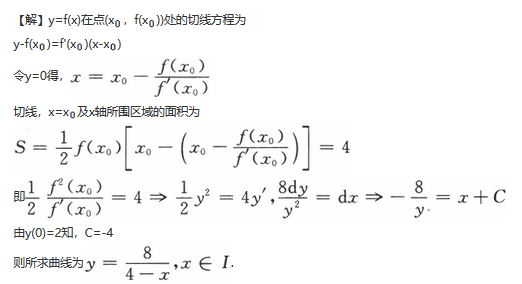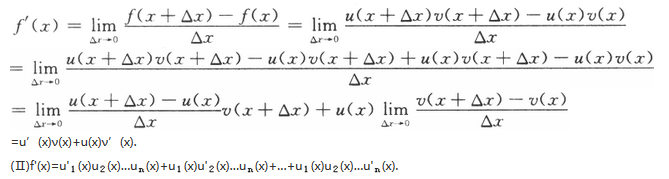设函数f(x)在(-∞,+∞)内连续,其二阶导函数f"(x)的图形如图所示,则曲线y=f(x)的拐点个数为
- A A0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:
由如图知f"(x1)=f"(x2)=0,f"(0)不存在,其余点上二阶导数f"(x)存在且非零,则曲线y=f(x)最多三个拐点,但在x=x1的两侧二阶导数不变号.因此,不是拐点,而在x=0和x=x2的两侧二阶导数变号,则曲线y=f(x)有两个拐点,故应选(C).
设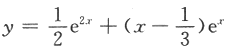 是二阶常系数非齐次线性微分方程
是二阶常系数非齐次线性微分方程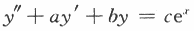 的一个特解,则
的一个特解,则
- A Aa=-3,b=2,c=-1
- B a=3,b=2,c=-1
- C a=-3,b=2,c=1
- D a=3,b=2,c=1
- 参考答案:A
- 您的答案:
参考解析:

【评注】其实,我们可看出齐次线性微分方程的特征根为1和2,非齐次线性微分方程的一个特解可为y=xe^x,进一步求得a,b,c.

- A A收敛点,收敛点
- B 收敛点,发散点
- C 发散点,收敛点
- D 发散点,发散点
- 参考答案:B
- 您的答案:
参考解析:

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
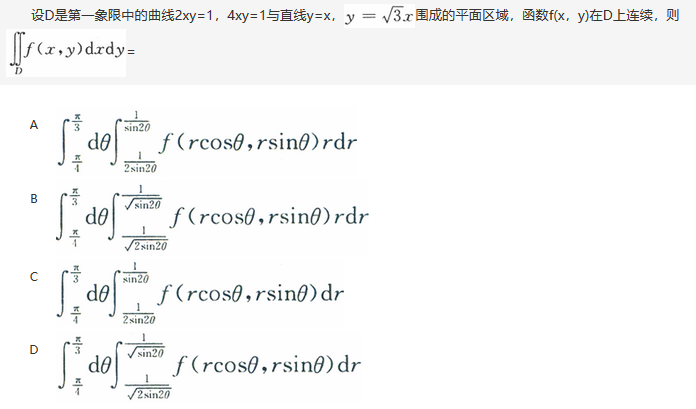
画出积分区域,用极坐标把二重积分化为二次积分. 曲线2xy=1,4xy=1的极坐标方程分别为
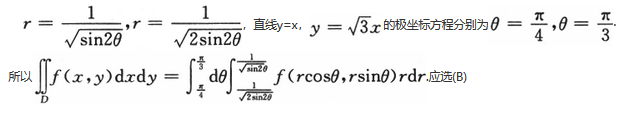

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

若A,B为任意两个随机事件,则
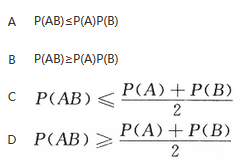
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

设随机变量X,Y不相关,且EX=2,EY=1,DX=3,则E[X(X+Y-2)]=
- A A-3
- B 3
- C -5
- D 5
- 参考答案:D
- 您的答案:
参考解析:
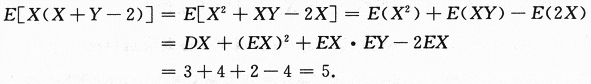
设函数f(x)=x+aln(1+x)+bxsinx,g(x)=kx^3,若f(x)与g(x)在x→0是等价无穷小,求a,b,k值.
设函数f(x)在定义域I上的导数大于零,若对任意的x0∈I,曲线y=f(x)在点(x0,f(x0))处的切线与直线x=x0及x轴所围成区域的面积恒为4,且f(0)=2,求f(x)的表达式.
已知函数f(x,y)=x+y+xy,曲线C:x^2+y^2+xy=3,求f(x,y)在曲线C上的最大方向导数.
- 参考答案:
- 您的答案:
参考解析:
【分析】函数在一点处沿梯度方向的方向导数最大,进而转化为条件最值问题
函数f(x,y)=x+y+xy在点(x,y)处的最大方向导数为
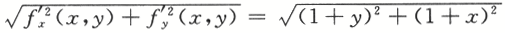
构造拉格朗日函数
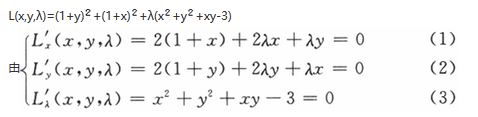
(2)-(1)得(y-x)(2+λ)=0
若y=x,则y=x=±1,若λ=-2,则x=-1,y=2或x=2,y=-1.
把两个点坐标代入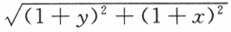 中,f(x,y)在曲线C上的最大方向导数为3.
中,f(x,y)在曲线C上的最大方向导数为3.
【评注】此题有一定新意,关键是转化为求条件极值问题.
(Ⅰ)设函数u(x),ν(x)可导,利用导数定义证明[u(x)ν(x)]’=u’(x)ν(x)+u(x)ν’(x);
(Ⅱ)设函数u1(x),u2(x),…,un(x)可导,f(x)=u1(x)u2(x)…un(x),写出f(x)的求导公式.
设随机变量X的概率密度为
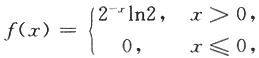
对X进行独立重复的观测,直到第2个大于3的观测值出现时停止,记Y为观测次数.
(Ⅰ)求Y的概率分布;
(Ⅱ)求EY.
- 参考答案:
- 您的答案:
参考解析:
【分析】令A={对X进行一次观测得到的值大于3}.

【评注】本题类似于我们在2000年出的几何分布考题.从建模到用幂级数在其收敛区间内可逐项求导求和会有不少考生感到困难,本题要比2000年的难一些.
设总体X的概率密度为
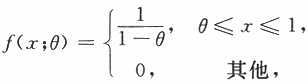
其中θ为未知参数,X1,X2,…,Xn,为来自该总体的简单随机样本.
(Ⅰ)求θ的矩估计量;
(Ⅱ)求θ的最大似然估计量.
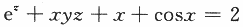 确定,则
确定,则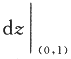 =_________.
=_________.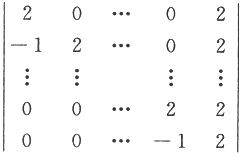 =_________.
=_________.