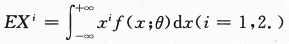下列曲线中有渐近线的是
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:

设函数f(x)具有二阶导数,g(x)=f(0)(1-x)+f(1)x,则在区间[0,1]上
- A A当f'(x)≥0时,f(x)≥g(x)
- B 当f'(x)≥0时,f(x)≤g(x)
- C 当f"(x)≥0时,f(x)≥g(x)
- D 当f"(x)≥0时,f(x)≤g(x)
- 参考答案:D
- 您的答案:
参考解析:
由于g(0)=f(0),g(1)=f(1),则直线y=f(0)(1-x)+f(1)x过点(0,f(0))和(1,f(1)),当f"(x)≥0时,曲线y=f(x)在区间[0,1]上是凹的,曲线y=f(x)应位于过两个端点(0,f(0))和(1,f(1))的弦y=f(0)(1-x)+f(1)x的下方,即f(x)≤g(x)故应选(D).
(方法二)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F'(x)=f'(x)+f(0)-f(1),F"(x)=f"(x).当f"(x)≥0时,F"(x)≥0,则曲线y=F(x)在区间[0,1]上是凹的.又F(0)=F(1)=0,从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).
(方法三)令F(x)=f(x)-g(x)=f(x)-f(0)(1-x)-f(1)x,
则 F(x)=f(x)[(1-x)+x]-f(0)(1-x)-f(1)x
=(1-x)[f(x)-f(0)]-x[f(1)-f(x)]
=x(1-x)f'(ξ)-x(1-x)f'(η) (ξ∈(0,x),η∈(x,1))
=x(1-x)[f'(ξ)-f'(η)]
当f"(x)≥0时,f'(x)单调增,f'(ξ)≤f'(η),从而,当x∈[0,1]时F(x)≤0,即f(x)≤g(x),故应选(D).

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
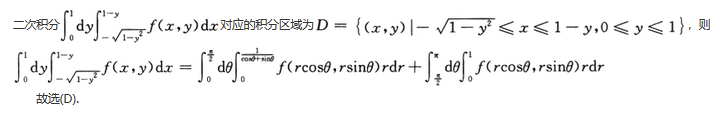
若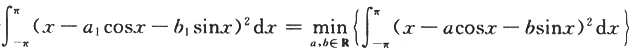 ,则a1cosx+b1sinx=
,则a1cosx+b1sinx=
- A A2sinx
- B 2cosx
- C 2πsinx
- D 2πcosx
- 参考答案:A
- 您的答案:
参考解析:



- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
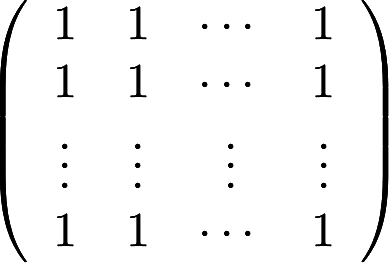
数字型行列式,有较多的0且有规律,应当有拉普拉斯公式的构思.

设α1,α2,α3均为三维向量,则对任意常数k,l,向量组α1+kα3,α2+lα3线性无关是向量组α1,α2,α3线性无关的
- A A必要非充分条件
- B 充分非必要条件
- C 充分必要条件
- D 既非充分也非必要条件
- 参考答案:A
- 您的答案:
参考解析:

设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=
- A A0.1
- B 0.2
- C 0.3
- D 0.4
- 参考答案:B
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
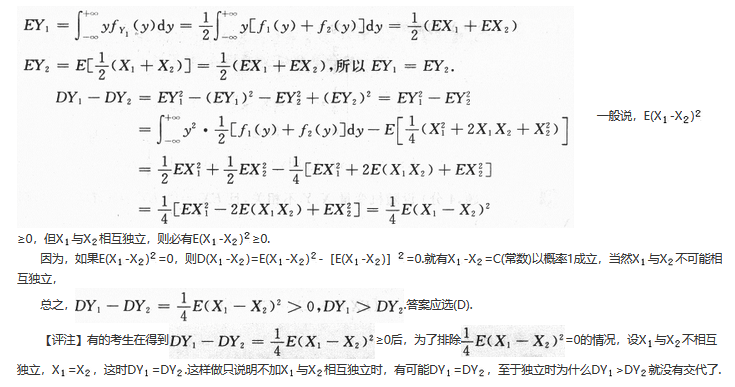
曲面z=x(1-siny)+y^2(1-sinx)在点(1,0,1)处的切平面方程为________.
设f(x)是周期为4的可导奇函数,且f'(x)=2(x-1),x∈[0,2],则f(7)=________.
微分方程xy’+y(lnx-lny)=0满足条件y(1)=e^3的解为y=________.
设函数f(u)具有二阶连续导数,z=f(e^xcosy)满足
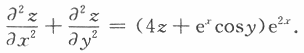
若f(0)=0,f'(0)=0,求f(u)的表达式.
设∑为曲面z=x^2+y^2(z≤1)的上侧,计算曲面积分
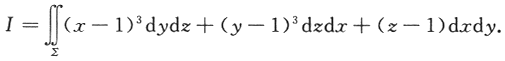
设A=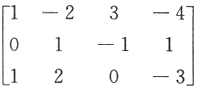 ,E为三阶单位矩阵.
,E为三阶单位矩阵.
(Ⅰ)求方程组Ax=0的一个基础解系;
(Ⅱ)求满足AB=E的所有矩阵B.
设随机变量X的概率分布为P{X=1}=P{X=2}=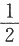 ,在给定X=i的条件下,随机变量Y服从均匀分布U(0,i)(i=1,2).
,在给定X=i的条件下,随机变量Y服从均匀分布U(0,i)(i=1,2).
(Ⅰ)求Y的分布函数FY(y);
(Ⅱ)求EY.
设总体X的分布函数为

其中θ是未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
(Ⅰ)求EX与EX^2;
(Ⅱ)求θ的最大似然估计量.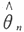
(Ⅲ)是否存在实数a,使得对任何ε>0,都有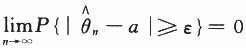 ?
?

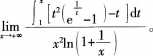
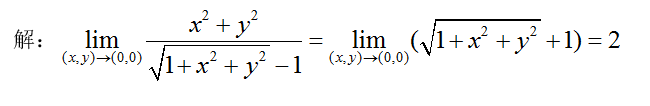
 与
与 相似
相似

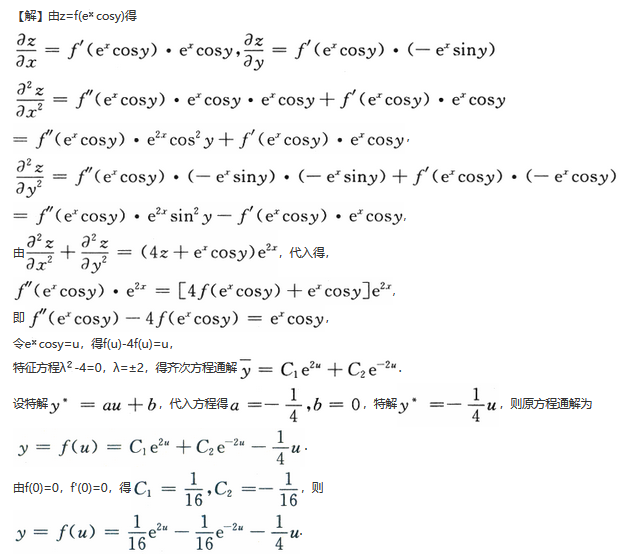

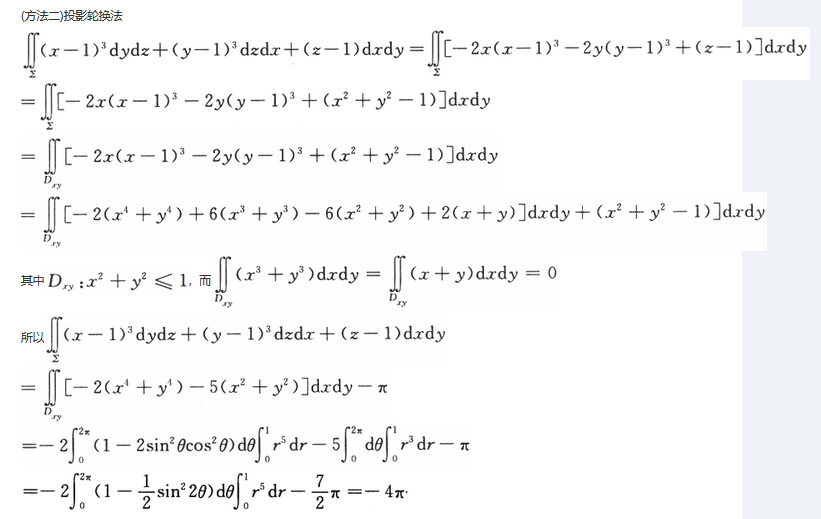


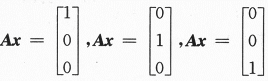 三个方程组的求解问题.
三个方程组的求解问题.