
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:

曲面x^2+cos(xy)+yz+x=0在点(0,1,-1)处的切平面方程为
- A Ax-y+z=-2
- B x+y+z=0
- C x-2y+z=-3
- D x-y-z=0
- 参考答案:A
- 您的答案:
参考解析:
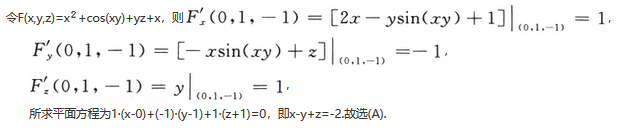

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:

设A,B,C均为n阶矩阵,若AB=C,且B可逆,则
- A A矩阵C的行向量组与矩阵A的行向量组等价
- B 矩阵C的列向量组与矩阵A的列向量组等价
- C 矩阵C的行向量组与矩阵B的行向量组等价
- D 矩阵C的列向量组与矩阵B的列向量组等价
- 参考答案:B
- 您的答案:
参考解析:
对矩阵A,C分别按列分块,记A=(α1,α2,…,αn),C=(γ,γ,…,γ). 由AB=C有
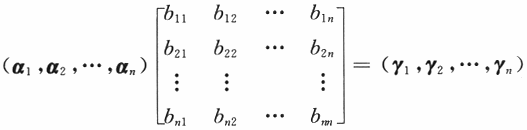
可见
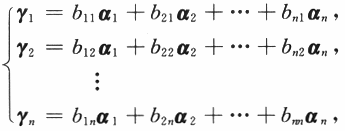
即C的列向量组可以由A的列向量组线性表出.
因为B可逆,有CB^-1=A.类似地,A的列向量组也可由C的列向量组线性表出,因此选(B).
矩阵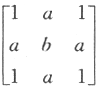 与
与 相似的充分必要条件为
相似的充分必要条件为
- A Aa=0,b=2
- B a=0,b为任意常数
- C a=2,b=0
- D a=2,6为任意常数
- 参考答案:B
- 您的答案:
参考解析:
两个实对称矩阵相似的充分必要条件是有相同的特征值.
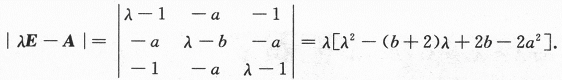
因为
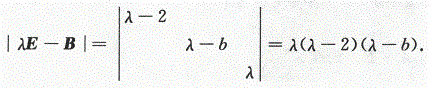
由λ=2必是A的特征值,即|2E-A|=2[2^2-2(b+2)+2b-2a^2]=0,故必有a=0.
由λ=b必是A的特征值,即|bE-A|=b[b^2-(b+2)b+2b]=0,b可为任意常数.
所以选(B).

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
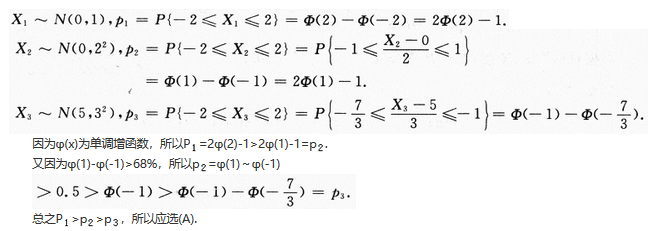
设随机变量X~t(n),Y~F(1,n),给定a(0
- A Aa
- B 1-a
- C 2a
- D 1-2a
- 参考答案:C
- 您的答案:
参考解析:
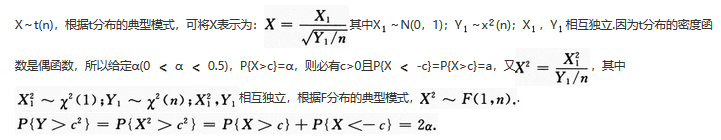
设函数y=f(x)由方程 确定,则
确定,则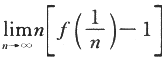 =________.
=________.
- 参考答案:1、1
- 您的答案:
参考解析:
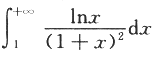 ________.
________.
- 参考答案:1、LN2.
- 您的答案:
参考解析:
设A=(aij)是三阶非零矩阵,|A|为A的行列式,Aij为aij的代数余子式,若aij+Aij=0(i,j=1,2,3),则|A|=________.
- 参考答案:1、-1.
- 您的答案:
参考解析:
求函数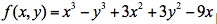 的极值
的极值
- 参考答案:
- 您的答案:
参考解析:






设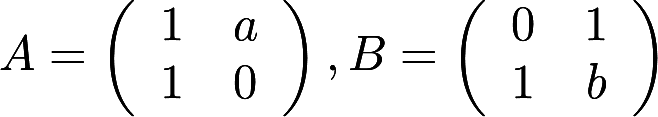 ,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C
,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C
- 参考答案:
- 您的答案:
参考解析:
由题意可知矩阵C为2×2阶矩阵,故可设


求所有矩阵C,即求出方程组①的通解。对方程组①的增广矩阵进行行初等变换:
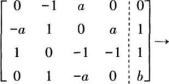
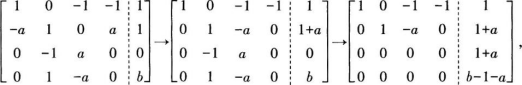
由于方程组①有解,故有1+

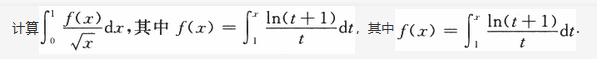
- 参考答案:
- 您的答案:
参考解析:

设数列{an}满足条件:a0=3,a1=1,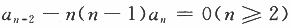 ,S(x)是幂级数
,S(x)是幂级数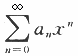 的和函数.
的和函数.
(Ⅰ)证明:S"(x)-S(x)=0;
(Ⅱ)求S(x)的表达式.
- 参考答案:
- 您的答案:
参考解析:
【分析】利用幂级数可逐项求导的性质,验证(Ⅰ)成立;解微分方程求出S(x),注意初值条件的使用.

设奇函数f(x)在[-1,1]上具有二阶导数,且f(1)=1,证明:
(Ⅰ)存在ξ∈(0,1),使得f'(ξ)=1;
(Ⅱ)存在η∈(-1,1),使得f"(η)+f'(η)=1.
- 参考答案:
- 您的答案:
参考解析:
【证明】(Ⅰ)因为f(x)是区间[-1,1]上的奇函数,所以f(0)=0.
因为函数f(x)在区间[0,1]上可导,根据拉格朗日中值定理,存在ξ∈(0,1),使得
f(1)-f(0)=f'(ξ).
又因为f(1)=1,所以f'(ξ)=1.
(Ⅱ)【证明】(方法一)因为f(x)是奇函数,所以f'(x)是偶函数,故f'(-ξ)=f'(ξ)=1.
令F(x)=[f'(x)-1]e^x,则F(x)可导,且F(-ξ)=F(ξ)=0.
根据罗尔定理,存在
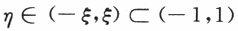
使得F'(η)=0.
由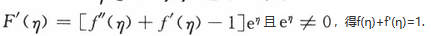
(方法二)因为f(x)是[-1,1]上的奇函数,所以f'(x)是偶函数,
令F(x)=f'(x)+f(x)-x,则F(x)在[-1,1]上可导,且
F(1)=f'(1)+f(1)-1=f'(1)
F(-1)=f'(-1)+f(-1)+1=f'(1)-f(1)+1=f'(1)
由罗尔定理可知,存在η∈(-1,1),使得F'(η)=0.
由F'(x)=f(x)+f'(x)-1,知
f(η)+f'(η)-1=0,f(η)+f'(η)=1.
(方法三)因为f(x)是[-1,1]上的奇函数,所以f'(x)是偶函数,f(x)是奇函数,由(Ⅰ)知,存在ξ∈(0,1),使得f'(ξ)=1.
令F(x)=f'(x)+f(x)-x,则F'(x)=f(x)+f'(x)-1,
F'(ξ)=f(ξ)+f'(ξ)-1=f(ξ)
F'(-ξ)=f(-ξ)+f'(-ξ)-1=-f(ξ)
当f(ξ)=0时,f(ξ)+f'(ξ)-1=0,即f(ξ)+f'(ξ)=1.结论得证.
当f(ξ)≠0时,F'(ξ)F'(-ξ)=-[f(ξ)]^2<0,
根据导函数的介值性,存在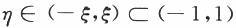 ,使得F'(η)=0.即f(η)+f'(η)-1=0
,使得F'(η)=0.即f(η)+f'(η)-1=0
故f(η)+f'(η)=1.
【评注】本题是一道微分中值定理的证明题,其难点在于(Ⅱ)中辅助函数的构造.欲证f(η)+f'(η)=1,只要证f(η)+(f'(η)-1)=0,即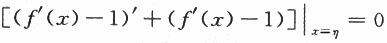 ,因此,应考虑辅助函数F(x)=[f'(x)-1]e^x;另一种思路是欲证f(η)+f'(η)=1,只要证f(η)+f'(η)-1=0,因此,应考虑辅助函数F(x)=f'(x)+f(x)-x.
,因此,应考虑辅助函数F(x)=[f'(x)-1]e^x;另一种思路是欲证f(η)+f'(η)=1,只要证f(η)+f'(η)-1=0,因此,应考虑辅助函数F(x)=f'(x)+f(x)-x.
方法三中用到达布定理即(导函数的的介值性),这个定理不是<考试大纲》要求的考试内容,部分考生给出了此种解法,只要书写正确,不影响得分.
设直线L过A(1,0,0),B(0,1,1)两点,将L绕z轴旋转一周得到曲面∑,∑与平面z=0,z=2所围成的立体为Ω.
(Ⅰ)求曲面∑的方程;
(Ⅱ)求Ω的形心坐标.
- 参考答案:
- 您的答案:
参考解析:
【分析】利用定义求旋转曲面∑的方程;利用三重积分求Ω的形心坐标.


- 参考答案:
- 您的答案:
参考解析:

设随机变量X的概率密度为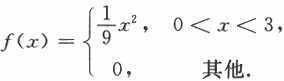 令随机变量
令随机变量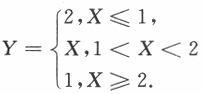 ,
,
(Ⅰ)求Y的分布函数;
(Ⅱ)求概率P{X≤Y}.
- 参考答案:
- 您的答案:
参考解析:
【分析】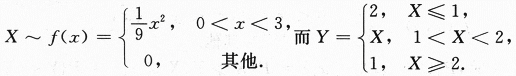
Y是随机变量X的函数,只是这函数是分段表示的,这样得到的Y可能是非连续型,也非离散型,
【解】(Ⅰ)设Y的分布函数为FYy),显然P{1≤Y≤2}=1,所以,
当y<1时,FY(y)=P{Y≤y)=0;
当1≤y<2时,FY(y)=P{Y≤y}=P{Y<1}+P{Y=1}+P{1 当2≤y时,FY(y)=P{Y≤y}=P{Y≤2}=1. 总之,Y的分布函数为 (Ⅱ)因为Y=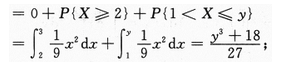
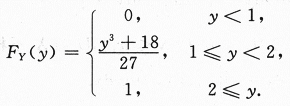
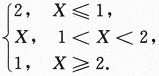
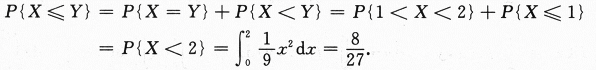
设总体X的概率密度为
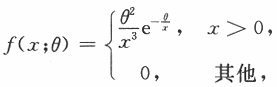
其中θ为未知参数且大于零.X1,X2,…,Xn为来自总体X的简单随机样本.
(Ⅰ)求θ的矩估计量;
(Ⅱ)求θ的最大似然估计量.
- 参考答案:
- 您的答案:
参考解析:

