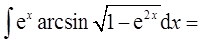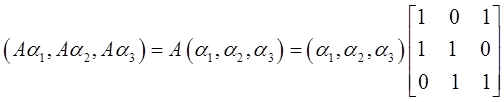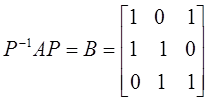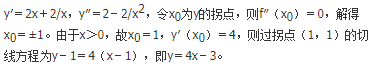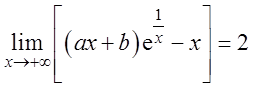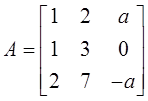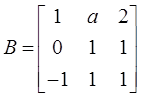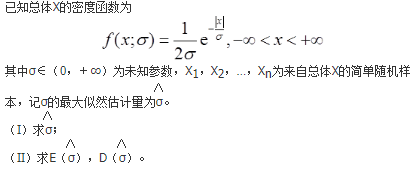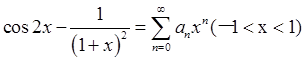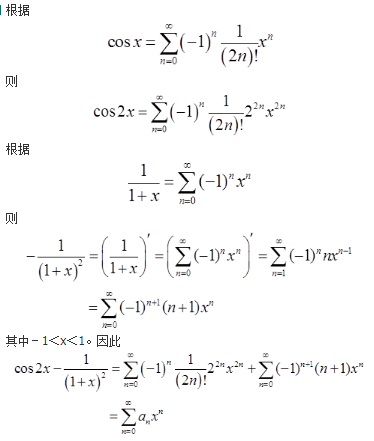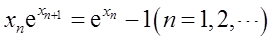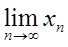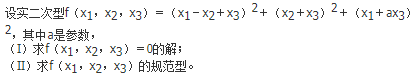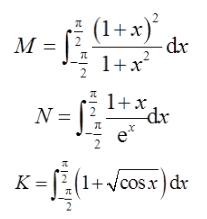 则( )。
则( )。
- A M>N>K
- B M>K>N
- C K>M>N
- D K>N>M
- 参考答案:C
- 您的答案:
参考解析:

设某产品的成本函数C(Q)可导,其中Q为产量,若产量为Q0时平均成本最小,则( )。

- A C′(Q0)=0
- B C′(Q0)=C(Q0)
- C C′(Q0)=Q0C(Q0)
- D Q0C′(Q0)=C(Q0)
- 参考答案:D
- 您的答案:
参考解析:

下列函数中,在x=0处不可导的是( )。
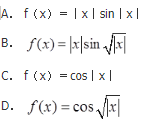
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
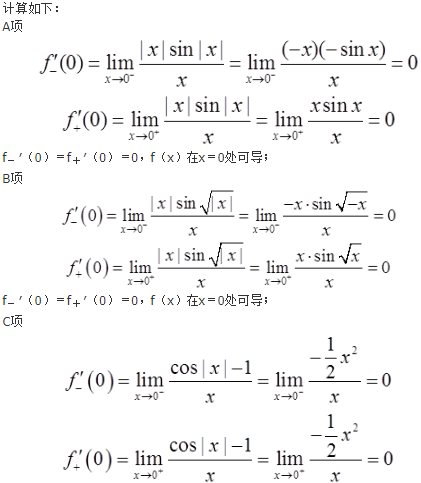

设函数f(x)在[0,1]上二阶可导,且
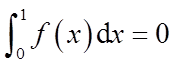
则( )。
- A 当f′(x)<0时,f(1/2)<0
- B 当f″(x)<0时,f(1/2)<0
- C 当f′(x)>0时,f(1/2)<0
- D 当f″(x)>0时,f(1/2)<0
- 参考答案:D
- 您的答案:
参考解析:


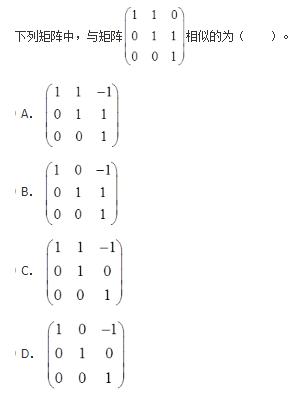
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:
题设矩阵记为X,4个选项矩阵分别记为A、B、C、D。矩阵X、A、B、C、D的三重特征值为1。
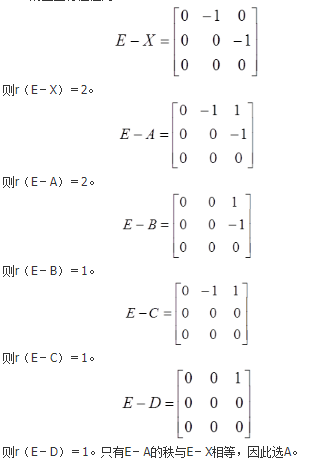
设A、B为n阶矩阵,记r(X)为矩阵X的秩,(X,Y)表示分块矩阵,则( )。
- A r(A,AB)=r(A)
- B r(A,BA)=r(A)
- C r(A,B)=max{r(A),r(B)}
- D r(A,B)=r(A^T,B^T)
- 参考答案:A
- 您的答案:
参考解析:
令AB=C,分块列阵为
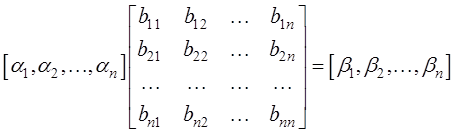
即β1,β2,…,βn,可由α1,α2,…,αn线性表出,矩阵的秩就是列向量组的秩。故r(A,AB)=r(α1,α2,…,αn,β1,β2,…,βn)=r(α1,α2,…,αn)=r(A)。
设随机变量X的概率密度f(x)满足f(1+x)=f(1-x),且

则P{X<0}=( )。
- A 0.2
- B 0.3
- C 0.4
- D 0.5
- 参考答案:A
- 您的答案:
参考解析:
由f(1+x)=f(1-x),知f(x)的图像关于x=1对称,利用特殊值法:将f(x)看成随机变量X~N(1,σ^2)的概率密度,根据正态分布的对称性,P{X<0}=0.2。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:

设A为3阶矩阵,α1,α2,α3为线性无关的向量组。若Aα1=α1+α2,Aα2=α2+α3,Aα3=α1+α3,则|A|=
设随机变量X与Y相互独立,X的概率分布为P{X=1}=P{X=-1}=1/2,Y服从参数为λ的泊松分布,令Z=XY。
(Ⅰ)求Cov(X,Z);
(Ⅱ)求Z的概率分布。
将长为2m的钢丝分为三段,依次围成成圆、正方形和正三角形,三个图形的面积之和是否存在最小值若存在,求出最小值。
- 参考答案:
- 您的答案:
参考解析:
设圆的半径为x,正方形边长为y,正三角形边长为z,则有2πx+4y+3z=2,其中x≥0,y≥0,z≥0。三个图形面积之和为
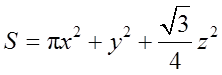
利用拉格朗日数乘法,建拉格朗日函数
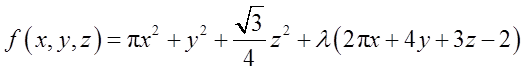
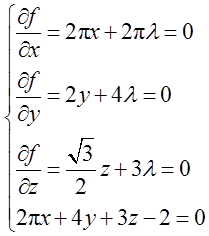
求解上述方程得到,驻点为
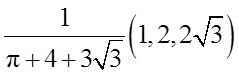
此时三个图形总面积最小,最小面积为
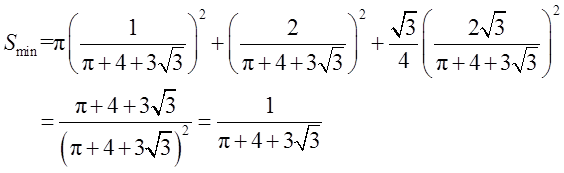
设函数f(x)满足f(x+Δx)-f(x)=2xf(x)Δx+ο(Δx)(Δx→0),且f(0)=2,则f(1)=