设函数f(x)可导,且f(x)f′(x)>0,则( )。
- A f(1)>f(-1)
- B f(1)<f(-1)
- C |f(1)|>|f(-1)|
- D |f(1)|<|f(-1)|
- 参考答案:C
- 您的答案:
参考解析:

若级数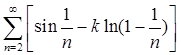 收敛,则k=( )。
收敛,则k=( )。
- A 1
- B 2
- C -1
- D -2
- 参考答案:C
- 您的答案:
参考解析:
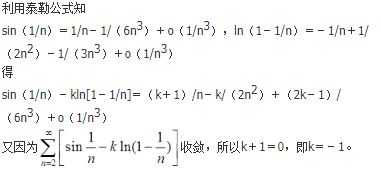
若函数
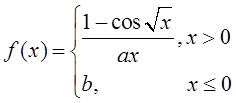
在x=0处连续,则( )。
- A ab=1/2
- B ab=-1/2
- C ab=0
- D ab=2
- 参考答案:A
- 您的答案:
参考解析:
二元函数z=xy(3-x-y)的极值点是( )。
- A (0,0)
- B (0,3)
- C (3,0)
- D (1,1)
- 参考答案:D
- 您的答案:
参考解析:

设α为n维单位列向量,E为n阶单位矩阵,则( )。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

已知矩阵
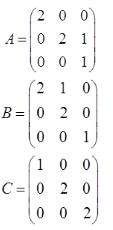
则( )。
- A A与C相似,B与C相似
- B A与C相似,B与C不相似
- C A与C不相似,B与C相似
- D A与C不相似,B与C不相似
- 参考答案:B
- 您的答案:
参考解析:
计算知A、B的特征值均为2、2、1,A有3个线性无关的特征向量,B只有2个,观察知C为对角矩阵,因此A与C相似,B与C不相似。
设A,B,C为三个随机事件,且A与C相互独立,B与C相互独立,则A∪B与C相互独立的充分必要条件是( )。
- A A与B相互独立
- B A与B互不相容
- C AB与C相互独立
- D AB与C互不相容
- 参考答案:C
- 您的答案:
参考解析:
由P((A∪B)∩C)=P(A∪B)P(C),P((A∪B)∩C)=P(AC∪BC)=P(AC)+P(BC)-P(AC∩BC)=P(AC)+P(BC)-P(ABC),而P(A∪B)P(C)=[P(A)+P(B)-P(AB)]P(C)=P(A)P(C)+P(B)P(C)-P(AB)P(C),可得P(ABC)=P(AB)P(C)。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
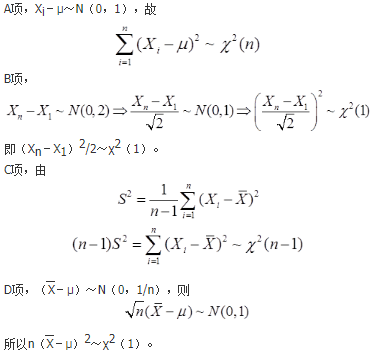
求极限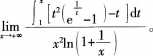
- 参考答案:
- 您的答案:
参考解析:
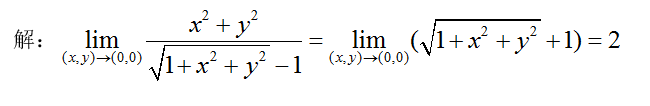
求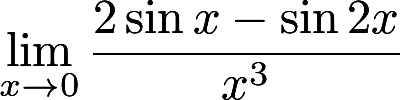
- 参考答案:
- 您的答案:
参考解析:

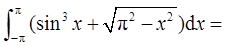
- 参考答案:
- 您的答案:
参考解析:
由对称区间上定积分的性质及定积分的几何意义可知
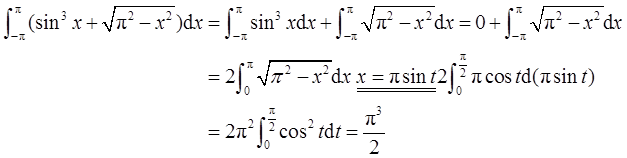

- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:
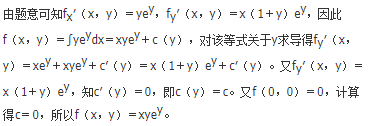
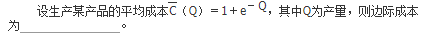
- 参考答案:
- 您的答案:
参考解析:
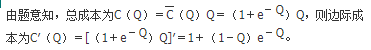

- 参考答案:
- 您的答案:
参考解析:
积分区域如图1所示,选用直角坐标计算该积分,先对y积分,后对x积分得
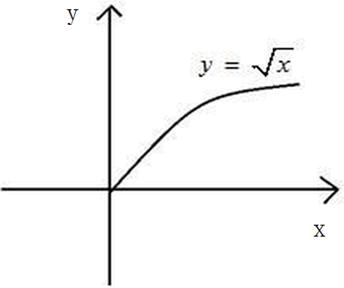
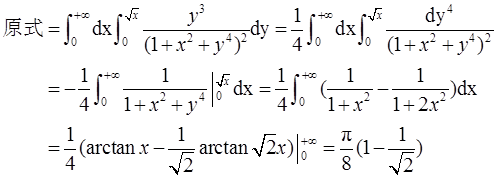

- 参考答案:
- 您的答案:
参考解析:


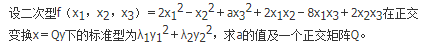
- 参考答案:
- 您的答案:
参考解析:



设随机变量X,Y相互独立,且X的概率分布为P(X=0)=P(X=2)=1/2,Y的概率密度为
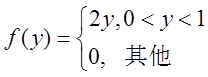
(Ⅰ)求P(Y≤EY);
(Ⅱ)求Z=X+Y的概率密度。
- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)计算得
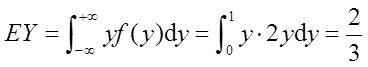
则

(Ⅱ)Z的分布函数为FZ(z)=P{Z≤z}=P{X+Y≤z,X=0}+P{X+Y≤z,X=2}=P{X=0,Y≤z}+P{X=2,Y+2≤z}=[P{Y≤z}+P{Y≤z-2}]/2=[FY(z)+FY(z-2)]/2。
故Z的概率密度函数为
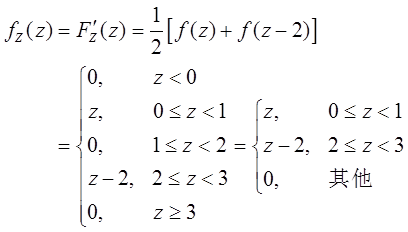
已知方程1/ln(1+x)-1/x=k在区间(0,1)内有实根,确定常数k的取值范围。
- 参考答案:
- 您的答案:
参考解析:

设3阶矩阵A=(α1,α2,α3)有3个不同的特征值,且α3=α1+2α2。
(Ⅰ)证明r(A)=2;
(Ⅱ)若β=α1+α2+α3,求方程组Ax=β的通解。
- 参考答案:
- 您的答案:
参考解析:


- 参考答案:
- 您的答案:
参考解析:


设随机变量X的概率分布为P{X=-2}=1/2,P{X=1}=a,P{X=3}=b,若EX=0,则DX=
- 参考答案:9/2
- 您的答案:
参考解析:
设矩阵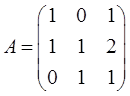
α1、α2、α3为线性无关的3维列向量组,则向量组Aα1、Aα2、Aα3的秩为
- 参考答案:2
- 您的答案:
