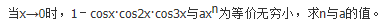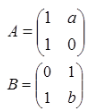- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:

当x→0时,用ο(x)表示比x的高阶无穷小,则下列式子中错误的是( )。
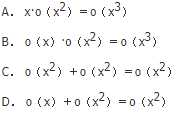
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:

设函数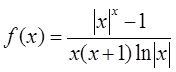 的可去间断点个数为( )。
的可去间断点个数为( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:


- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:B
- 您的答案:
参考解析:
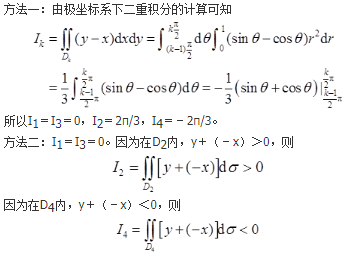
设矩阵A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )。
- A 矩阵C的行向量组与矩阵A的行向量组等价
- B 矩阵C的列向量组与矩阵A的列向量组等价
- C 矩阵C的行向量组与矩阵B的行向量组等价
- D 矩阵C的列向量组与矩阵B的列向量组等价
- 参考答案:B
- 您的答案:
参考解析:
把矩阵A,C列分块如下:A=(α1,α2,…,αn),C=(γ1,γ2,…,γn),由于AB=C,则可知γi=bi1α1+bi2α2+…+binαn(i=1,2,…,n),得到矩阵C的列向量组可用矩阵A的列向量组线性表示,同时由于B可逆,即A=CB-1,同理可知矩阵A的列向量组可用矩阵C的列向量组线性表示,所以矩阵C的列向量组与矩阵A的列向量组等价。
矩阵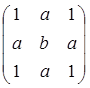 和
和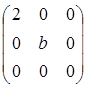 相似的充分必要条件为( )。
相似的充分必要条件为( )。
- A a=0,b=2
- B a=0,b为任意常数
- C a=2,b=0
- D a=2,b为任意常数
- 参考答案:B
- 您的答案:
参考解析:
注意矩阵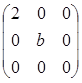 是对角矩阵,所以矩阵
是对角矩阵,所以矩阵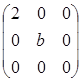 与矩阵相似的充分必要条件是两个矩阵的特征值对应相等。
与矩阵相似的充分必要条件是两个矩阵的特征值对应相等。
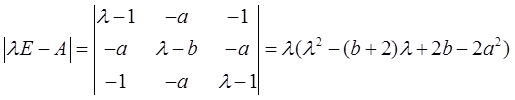
故可知2b-2a2=2b,即a=0,b为任意常数。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:A
- 您的答案:
参考解析:

设随机变量X和Y相互独立,且X和Y的概率分布分别如表1和表2所示。
表1

表2
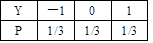
则P{X+Y=2}=( )。
- A 1/12
- B 1/8
- C 1/6
- D 1/2
- 参考答案:C
- 您的答案:
参考解析:
由题意知,P{X+Y=2}=P{X=1,Y=1}+P{X=2,Y=0}+P{X=3,Y=-1}=(1/4)×(1/3)+(1/8)×(1/3)+(1/8)×(1/3)=1/6。
设A=(aij)是三阶非零矩阵,|A|为A的行列式,Aij为aij的代数余子式,若aij+Aij=0(i,j=1,2,3),则|A|=
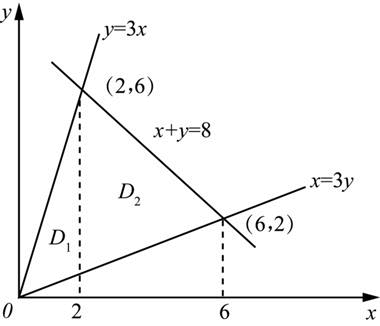
设平面内区域D由直线x=3y,y=3x及x+y=8围成,计算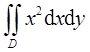
- 参考答案:
- 您的答案:
参考解析:
直线x+y=8与直线y=3x和x=3y分别交于点(2,6)和(6,2),直线x=2将区域D分为D1和D2两部分(如图1所示),则有
说明:说明:13-1
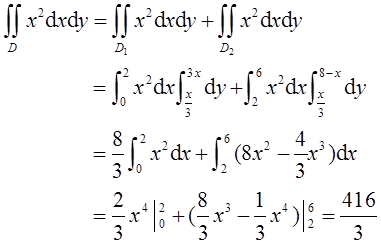
设生产某产品的固定成本为6000元,可变成本为20元/件,价格函数为P=60-Q/1000,(P是单价,单位:元;Q是销量,单位:件),已知产销平衡,求:
(Ⅰ)该商品的边际利润;
(Ⅱ)当P=50时的边际利润,并解释其经济意义;
(Ⅲ)使得利润最大的定价P。
- 参考答案:
- 您的答案:
参考解析:
(Ⅰ)设利润为y,则y=PQ-(6000+20Q)=40Q-Q2/1000-6000,边际利润为y′=40-Q/500。
(Ⅱ)当P=50时,Q=10000,边际利润为20,其经济意义为:当P=50时,每增加1件的销量可以增加20元的利润。
(Ⅲ)利润最大化的条件是边际收益等于边际成本。令y′=0,得Q=20000,P=60-20000/1000=40(元)。
设总体X的概率密度为
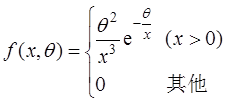
其中θ为未知参数且大于零,X1,X2,…Xn为来自总体X的简单随机样本。
(Ⅰ)求θ的矩估计量;
(Ⅱ)求θ的最大似然估计量。