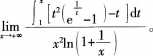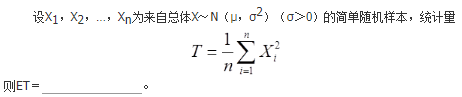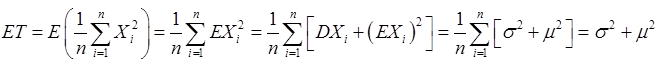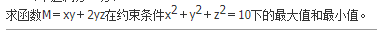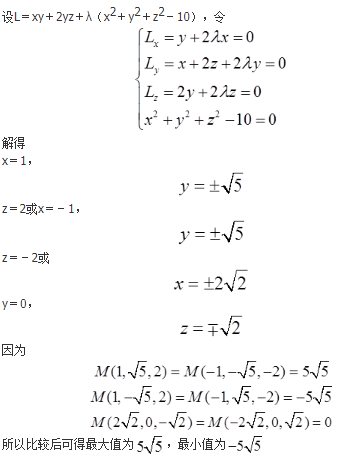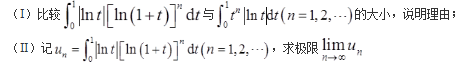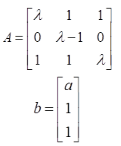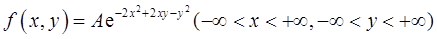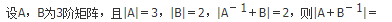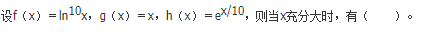
- A g(x)<h(x)<f(x)
- B h(x)<g(x)<f(x)
- C f(x)<g(x)<h(x)
- D g(x)<f(x)<h(x)
- 参考答案:C
- 您的答案:
参考解析:
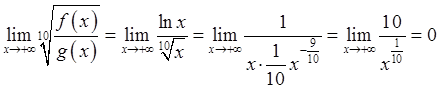
于是,当x充分大时,f(x)<g(x);

于是,当x充分大时,g(x)<h(x)。故选C项。
设向量组(Ⅰ)α1,α2,…αr,可由向量组(Ⅱ)β1,β2,…βs线性表示,则( )。
- A 若向量组(Ⅰ)线性无关,则r≤s
- B 若向量组(Ⅰ)线性相关,则r>s
- C 若向量组(Ⅱ)线性无关,则r≤s
- D 若向量组(Ⅱ)线性相关,则r>s
- 参考答案:A
- 您的答案:
参考解析:
向量组(Ⅰ)α1,α2,…αr,可由向量组(Ⅱ)β1,β2,…βs线性表示,则
r(α1,α2,…αr)≤r(β1,β2,…βs)≤s
对选项A,若向量组(Ⅰ)线性无关,则r(α1,α2,…αr)=r,故r≤s,即选A项。
若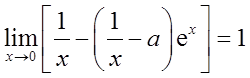 则a等于( )。
则a等于( )。
- A 0
- B 1
- C 2
- D 3
- 参考答案:C
- 您的答案:
参考解析:
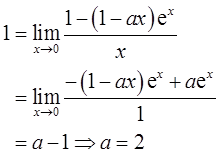
设y1,y2为一阶非齐次线性微分方程y′+p(x)y=q(x)的两个特解,若存在λ,μ使λy1+μy2为该方程的解,λy1-μy2为该方程对应齐次微分方程的解,则( )。
- A λ=1/2,μ=1/2
- B λ=-1/2,μ=-1/2
- C λ=2/3,μ=1/3
- D λ=2/3,μ=2/3
- 参考答案:A
- 您的答案:
参考解析:
因为y1,y2为一阶非齐次线性微分方程y′+p(x)y=q(x)的两个特解,所以
y1′+p(x)y1=q(x),y2′+p(x)y2=q(x)①
λy1+μy2为该方程的解,则(λy1+μy2)′+p(x)(λy1+μy2)=q(x)。将①代入上式可得λ+μ=1②,λy1-μy2为该方程对应齐次微分方程的解,则(λy1-μy2)′+p(x)(λy1-μy2)=0。将①代入上式可得λ-μ=0③,由②和③可得λ=μ=1/2,故选A项。
设函数f(x),g(x)具有二阶导数,且g″(x)<0,g(x0)=a是g(x)的极值,则f(g(x))在x0取到极大值的一个充分条件是( )。
- A f′(a)<0
- B f′(a)>0
- C f″(a)<0
- D f″(a)>0
- 参考答案:B
- 您的答案:
参考解析:
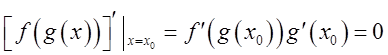
即x=x0是f(g(x))的驻点。
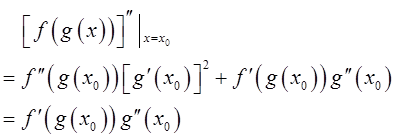
若想要f(g(x))在x0取到极大值,只要f′(g(x0))g″(x0)<0,即f′(g(x0))>0,于是f′(a)>0是一个充分条件,故选B项。

- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:C
- 您的答案:
参考解析:
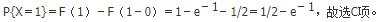
设A为四阶实对称矩阵,且A2+A=O,若A的秩为3,则A相似于( )。
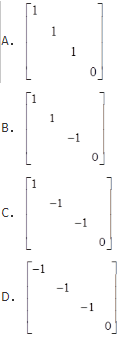
- A 见图A
- B 见图B
- C 见图C
- D 见图D
- 参考答案:D
- 您的答案:
参考解析:
因为A为4阶实对称矩阵,所以A必可相似对角化,且A的特征值全为实数。设λ为A的特征值,则λ2+λ=0λ=0或λ=-1。又A的秩为3,则A的特征值为-1,-1,-1,0,故选D项。
设f1(x)是标准正态分布的概率密度函数,f2(x)是[-1,3]上均匀分布的概率密度,且
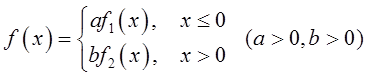
为概率密度,则a,b应满足( )。
- A 2a+3b=4
- B 3a+2b=4
- C a+b=1
- D a+b=2
- 参考答案:A
- 您的答案:
参考解析:
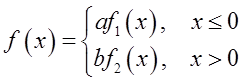
所以
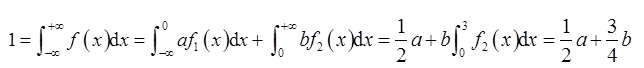
于是2a+3b=4,故选A项。
箱中装有6个球,其中红、白、黑球的个数分别为1,2,3个,现从箱中随机地取出2个球,记X为取出的红球个数,Y为取出的白球个数。
(Ⅰ)求随机变量(X,Y)的概率分布;
(Ⅱ)求Cov(X,Y)。

- 参考答案:
- 您的答案:
参考解析:

(Ⅱ)f(x)在闭区间[2,3]上连续,从而在该区间存在最大值M和最小值m,于是m≤f(2)≤M,m≤f(3)≤Mm≤[f(2)+f(3)]/2≤M。
由介值定理可得存在ζ∈[2,3],使得f(ζ)=[f(2)+f(3)]/2,于是f(0)=f(η)=f(ζ),η∈(0,2),ζ∈[2,3]。函数f(x)在[0,η],[η,ζ]均满足罗尔定理,所以存在ξ1∈(0,η),ξ2∈(η,ζ),使得f′(ξ1)=f′(ξ2)=0。函数f′(x)在[ξ1,ξ2]满足罗尔定理,故存在ξ∈(ξ1,ξ2)(0,3),使得f″(ξ)=0。