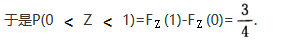设X,Y相互独立且都服从(0,2)上的均匀分布,令Z=min{X,Y},则P(0
正确答案及解析
正确答案
解析
由X,Y在(0,2)上服从均匀分布得 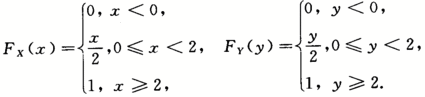
因为x,Y相互独立,所以
Fz(z)=P(Z≤z)=1-P(Z>z)=1-P(min{X,Y)}>z)=1-P(X>z,Y>z)
=1-P(X>z)P(Y>z)=1=【1-P(X≤z)】【1-P(Y≤z)】
=1-【1-Fx(z)】【1-FY(z)】,
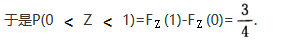
设X,Y相互独立且都服从(0,2)上的均匀分布,令Z=min{X,Y},则P(0
由X,Y在(0,2)上服从均匀分布得 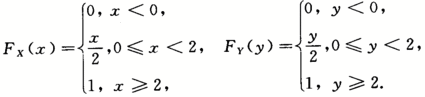
因为x,Y相互独立,所以
Fz(z)=P(Z≤z)=1-P(Z>z)=1-P(min{X,Y)}>z)=1-P(X>z,Y>z)
=1-P(X>z)P(Y>z)=1=【1-P(X≤z)】【1-P(Y≤z)】
=1-【1-Fx(z)】【1-FY(z)】,