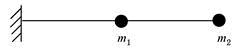
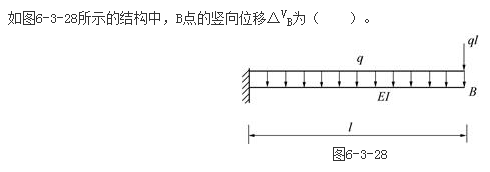
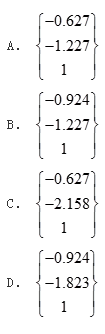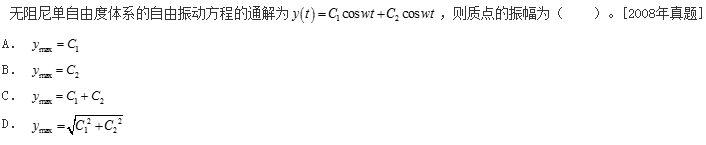无向图G=(V,E),其中V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是()。
- A.a,b,e,c,d,f
- B.a,c,f,e,b,d
- C.a,e,b,c,f,d
- D.a,e,d,f,c,b
正确答案及解析
正确答案
C
解析
假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点v,并将其标记为已访问过:然后依次从v出发搜索v的每个邻接点w。若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。