f(x)=2x3-9x2+12x-3的单调增加区间为()。
- A.(1,2)
- B.(-∞,1)
- C.(0,+∞)
- D.(-∞,1)与(2,+∞)
正确答案及解析
正确答案
D
解析
由f'(x)=6x2-18x+12=6(x-1)(x-2)
当x<1,f'(x)>0,所以f(x)在(-∞,1)上单调增加,
当1<x<2,f'(x)<0,所以f(x)在(1,2)上单调下降,
当x>2,f'(x)>0,所以f(x)在(2,+∞)上单调增加
包含此试题的试卷
你可能感兴趣的试题
设A、B、C为三个事件,则A、B、C中至少有两个发生可表示为:
-
- A.AUBUC
- B.A(BUC)
- C.ABUACUBC <img src='http://tp.mxqe.com/data/830/13984487_0.jpg' alt='军队文职数学1,专项练习,军队文职招聘《数学1》高数' title='军队文职数学1,专项练习,军队文职招聘《数学1》高数'>
- 查看答案

-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案
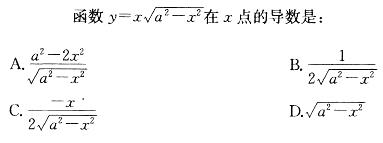
-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案
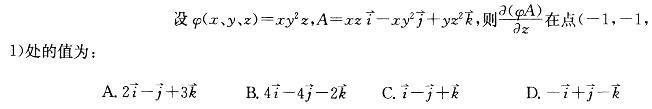
-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案
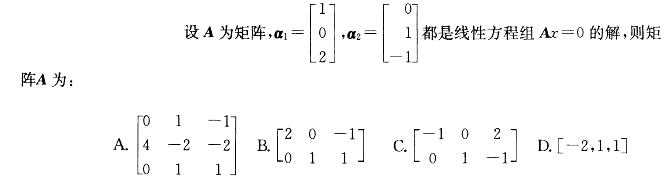
-
- A.见图A
- B.见图B
- C.见图C
- D.见图D
- 查看答案