教学设计。
《义务教育数学课程标准(2011年版)》在课程内容中要求:创新意识的培养是现代数学教育的根本任务,应体现在数学教与学的过程之中,学生自己发现问题和提出问题是创新的基础;独立思考、学会思考是创新的核心;归纳概括得到猜想和规律,并加以验证是创新的重要方法。
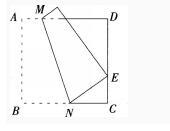
素材:如图所示,将正方形纸片ABCD折叠,使B点落在CD边上一点E(不与C,D重合),压平后得到折痕删。
(1)试根据点E在CD上的位置变化,设置适当条件,编制一道数学题目;(不要求解答)
(2)依据上述素材和要求,试以提出问题为主线进行“探究式”解题教学,撰写一份培养学生观察与发现,归纳与推理能力的教学过程设计。(只需写出教学过程,突出探究的方法与问题即可)
正确答案及解析
正确答案
解析
(1)本题具有开放性,题目设置合理即可,下面是几个示例: 设正方形纸片ABCD边长为2,
 (2)导入:
(2)导入:
采用练习导人法.利用一个简单的练习题引入本节课内容。
新课讲授:
根据导入的例题,提出问题:在之前学习的三角形知识中,有哪些常用的性质和定理?
预设:①全等三角形判定定理,②相似三角形判定定理,③等腰三角形性质,④勾股定理……
找学生回答并追问,明确具体的性质和定理内容。
在复习之前的知识之后,结合(1)中②③进行“探究式”解题教学。
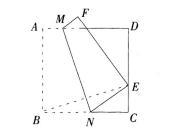
给出例题:如图所示,已知正方形纸片ABCD边长为2,将正方形纸片ABCD折叠,使曰点落在CD边上一点E(不与C,D重合),压平后得到折痕MN,A点落在点F处。
问题1:根据条件,能够获得哪些结论?
学生七嘴八舌地说着,教师提问后总结

问题6:求E在什么位置时,△ENC的面积取得最大值?
之前的几个问题都是为了解决问题6做铺垫的,在前五个问题的基础上研究问题6,几何问题已经转化成函数求最值问题.即求函数 的最大值。
计算部分留给学生。教师对本节课做小结:同学们,我们在学习数学的过程中要善于独立思考,学会在已知条件的基础上归纳概括得出猜想和规律,发现问题、提出问题并想办法去解决问题。要大胆的去尝试,把看起来难的问题。细化成若干个可以解决的小问题,在不断探究不断深入的过程中就会自然而然地解决问题。
作业:已知正方形ABCD边长为2,将正方形纸片ABCD折叠,使B点落在CD边上一点E(不与C,D重合),

包含此试题的试卷
你可能感兴趣的试题
“有为才有位,有位更有为”,这一看法给我们的启示是( )
-
- A.实践决定认识,认识对发展具有推动作用
- B.实现人生价值必须先要实现人的自我价值
- C.人生真正价值在于社会价值与自我价值的统一
- D.要发挥主观能动性,要不断积累自我价值
- 查看答案
历史唯物主义认为人的价值在于( )
-
- A.个人的自我创造和自我实现
- B.个人的自我选择和自由发展
- C.个人主体性的增强和摆脱社会的制约
- D.个人对社会的贡献和社会对个人的尊重
- 查看答案
对立统一规律揭示了事物发展的( )。
-
- A.辩证形式
- B.趋势和道路
- C.不同状态
- D.源泉和动力
- 查看答案
矛盾的普遍性与特殊性的关系是( )
-
- A.一般与个别的关系
- B.整体与局部的关系
- C.绝对与相对的关系
- D.可以相互转化的关系
- 查看答案
在认识过程中具有更为重要意义的飞跃是指()
-
- A.从外在形象到内在本质的飞跃
- B.从个性认识到共性认识的飞跃
- C.从肯定阶段到否定阶段的飞跃
- D.从理性认识到实践的飞跃
- 查看答案