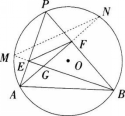
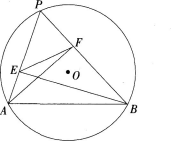
如图,点P为⊙O上一动点,PA,PB为⊙O的两条弦,BE,AF分别垂直于PA,PB,垂足分别为E,F,若∠P=60°,⊙O的半径为4,则EF的长( )。

- A.见图A
- B.见图B
- C.见图C
- D.见图D
正确答案及解析
正确答案
C
解析
BE,AF的交点记为G,G即是△ABC垂心,则G点关于AP,BP两条边的对称点M,N都在△ABC外接圆⊙O上。(三角形的垂心关于三边的对称点都在三角形的外接圆上。)则EF是△GMN平行于 MN边的中位线,则EF∥MN,所以∠FEB=∠M=∠FAB。 又因为G为垂心,所以∠PEF+∠FEB=∠FAB+∠PBA=90°,所以∠PEF=∠PBA。所以△PEF∽△PBA,于是