依据以下要求和素材,撰写侧重培养能力的教学过程设计(只要求写出教学过程)。
素材:教师用多媒体呈现一条射线绕着它的端点旋转,得到许多大小不一样的角,提出这样的问题:同学们,你们能帮这些角分一分吗?好,我们就一起来分一分。
正确答案及解析
正确答案
解析
一、创设情境,导入新课
课件出示一些实际生活中角的图片
提问:能不能从这些图片中找到角呢?
引导学生从图片中找到角,并通过多媒体呈现这些角。
提问:同学们,能对以上的这些角进行分类吗?
学生按照自己的标准进行分类。
教师:同学们都有自己的分类方法,那么今天就跟老师一起来学习老师使用的角的分类方法吧。
二、讲授新课
1、认识直角
拿出一些直角三角形纸片,让学生量一量最大的角的度数。
学生操作后回答:
板书直角的定义:1直角=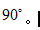
提问:同学们,说一说身边都有哪些角是直角?
2、认识锐角和钝角
拿出一把折扇,一边不动,一边围绕顶点旋转,旋转到折扇两边成90°时,继续旋转,直到两条边成一条直线。
我们把小于的角叫钝角。
用大屏幕呈现一些角,让学生观察哪些角是锐角,哪些角是钝角。
3.认识平角
用折扇再次进行旋转,当折扇的两条边在一条直线上时,提问:这是不是一个角?这个角是多少度?
当角的两边成一条直线,这样的角叫平角,平角是180°。
给学生一个能够活动的量角器,让学生转出一个平角
3.认识周角
继续旋转折扇,当两条边重合时,提问:这是角吗?这个角是多少度?
当角的两条边重合时,就形成了一个周角,周角为360°。
让学生继续用活动的量角器转出一个周角。
提问:那么直角、平角、周角之间有什么关系呢?
1个周角=2个平角=4个直角。
提问:同学们,能将以上所学的角按度数大小进行排序吗?
学生分组讨论,找小组代表回答,其他小组进行点评。
三、巩固练习,内化提高
1.选一选,把小面的角的度数分别填在适当的括号里。
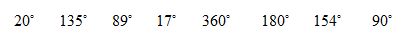
锐角( ),直角( ),钝角( ),周角( )
2.判断对错
①大于90度的角叫钝角。 ( )
②平角的一半是直角。 ( )
③两个锐角的和一定是钝角。 ( )
学生独立练习,对于基础差的学生,给予适当的指导。
四、回顾整理,反思提升
老师提问,学生作答。
(1)本节课学习了锐角、直角、钝角、直角、平角、周角;
(2)锐角<直角<钝角<直角<平角<周角;
(3)1个周角=2个平角=4个直角。
五、作业布置
1、课后习题43页做一做第1题;
2、回家自己画10个不同的角,并对这些角进行分类。
你可能感兴趣的试题
“有为才有位,有位更有为”,这一看法给我们的启示是( )
-
- A.实践决定认识,认识对发展具有推动作用
- B.实现人生价值必须先要实现人的自我价值
- C.人生真正价值在于社会价值与自我价值的统一
- D.要发挥主观能动性,要不断积累自我价值
- 查看答案
历史唯物主义认为人的价值在于( )
-
- A.个人的自我创造和自我实现
- B.个人的自我选择和自由发展
- C.个人主体性的增强和摆脱社会的制约
- D.个人对社会的贡献和社会对个人的尊重
- 查看答案
对立统一规律揭示了事物发展的( )。
-
- A.辩证形式
- B.趋势和道路
- C.不同状态
- D.源泉和动力
- 查看答案
矛盾的普遍性与特殊性的关系是( )
-
- A.一般与个别的关系
- B.整体与局部的关系
- C.绝对与相对的关系
- D.可以相互转化的关系
- 查看答案
在认识过程中具有更为重要意义的飞跃是指()
-
- A.从外在形象到内在本质的飞跃
- B.从个性认识到共性认识的飞跃
- C.从肯定阶段到否定阶段的飞跃
- D.从理性认识到实践的飞跃
- 查看答案