1.阅读下面案例，回答问题：两位教师上“圆的认识”一课。教师-名校题库网

题目详情

全站导航

首页试卷试题资讯

试卷导航

建筑工程职业资格公务员财会类医卫类外语类计算机类学历类

试题导航

建筑工程职业资格公务员财会类医卫类外语类计算机类学历类

1.阅读下面案例，回答问题：

两位教师上“圆的认识”一课。

教师A：

在教学“半径和直径关系”时，组织学生动手测量、指一指、标一标，然后引导学生发现“在同一圆中，圆的半径是直径的一半”。

教师B：

师：通过自学，你知道半径和直径的关系吗？

生1：在同一圆里，所有的半径都是直径的一半。

生2：在同一圆里，所有的直径是半径的2倍。

生3：如果用字母表示，则是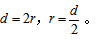小学教师招聘,押题密卷,2021年教师招聘考试《小学数学》押题密卷7

师：这是同学们通过自学获得的，你们能用什么方法证明这一结论是正确的。

生1：我可以用尺子测量一下直径和半径的长度，然后考查它们之间的关系。

师：那我们一起用这一方法检测一下。

……

师：还有其他方法吗？

生2：通过折纸，我能看出它们的关系。

……

（1）两个案例的主要共同点是什么？

（2）结合案例，谈谈教师A和教师B是否真正了解学生的起点？并说明理由。

（3）预测两位教师采用的教学方法所达到的教学效果？并说明在数学教学实践中，你会采用怎样的教学方法来进行教学？

正确答案及解析

正确答案

解析

（1）共同点：两个案例都注重学生的实践操作。教师A组织学生动手测量、指一指、标一标，通过动手操作来理解直径和半径的特征及联系。教师B启发学生自主思考探究的方法，利用尺子测量或折纸的方法来探究直径和半径的关系。两个案例都注重学生动手操作能力方面的培养。

（2）案例中A教师和B教师没有真正的了解学生的起点，A教师是基于学生在学习了三角形、平行四边形、长方形、正方形的基础之上来学习圆，并运用了一贯的动手测量、指一指、标一标的探究思路，然后引导学生发现结论。学生在此过程中没有收获新的思想方法，是一种吃不饱的状态。“认识圆”是六年级的课程内容，学生已有了一定的抽象思维能力，因此，在教学过程中，不仅要注重学生几何直观能力的培养，更应注重学生抽象思维能力的培养。教学过程是教师的教与学生学的互动过程，教师是教学活动的组织者引导者合作者，A教师先让学生自学“半径和直径关系”，然后让学生汇报，没有教师的层层引导，没有考虑到学生的基础知识水平，即学生的知识起点；B教师让学生自学，这高估了学生的基础，虽然学生之前已经学习了三角形、平行四边形、长方形、正方形的知识，但是与圆的知识还有很大的区别，自学起来相对比较难，所以在学习过程中，学习基础差的学生自学起来是比较吃力的，需要教师的引导和帮助，因此B教师也没有真正了解学生。

（3）第一位老师的教学效果，学生通过学习本节课掌握了基本知识和基本技能，也调动了学生的积极性，学生自主参与到教学活动中，激发了学生的学习兴趣。但是在教学过程中，缺乏对学生基本思想方法的培养，学生的抽象思维能力没有得到很好的发展。第二位老师为学生创设了一次比较成功的数学活动，我们可以预测这样的活动一定能让学生感受到数学的无穷魅力。

在数学教学实践中，我会注重培养学生的基本知识、基本技能、基本思想、基本活动经验。一方面承接了学生原有的认知经验，学生感受到数学很简单、很日常、很好玩，有信心、有兴趣去学习。另一方面，学生通过多感官的活动，探究这些亲切有趣的现象背后的原理，丰富了学生的几何直观，提高了学生的抽象思维能力。