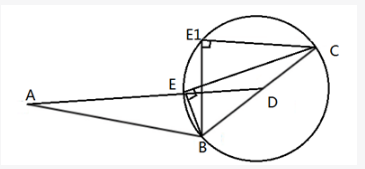
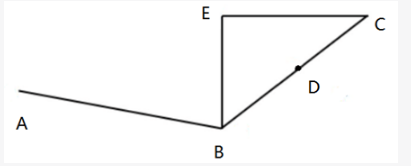
人行道ABC,BC长286cm,D为BC中点。AD直线距离为324cm,过B点做直线BE,过C点做垂线与BE交于E点,问AE最小距离为多少?
- A.38cm
- B.168cm
- C.176cm
- D.181cm
正确答案及解析
正确答案
D
解析
第一步,本题考查几何问题,属于平面几何类。
第二步,如图所示,E点的轨迹应该是一个以BC为直径、D为圆心的半圆。最短的距离为AD连线交圆于E点的AE,此距离为324-ED。在直角三角形BEC中DE是斜边的中线,距离是斜边的一半即286÷2=143cm,则最短距离为324-143=181cm。