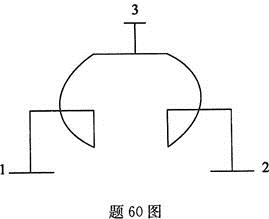
如图所示，分裂电抗器中间抽头3接电源，两个分支1和2接相等的两组负荷，两个分支的自感电抗相同，均为Xk，耦合系数K取0.5，下列表达哪项正确（ ）
- A.正常运行时，电抗器的电抗值为0.25Xk
- B.当分支1出现短路时，电抗器的电抗值为2Xk
- C.当分支1出现短路时，电抗器的电抗值为1.5Xk
- D.正常运行时，电抗器的电抗值为Xk；当分支1出现短路时，电抗器的电抗值为3Xk
正确答案及解析
正确答案
A
解析
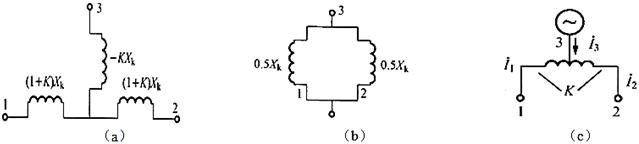
由题图知分裂电抗器的结构相当于两支电抗器连接在一起，线圈的每半段为一分支，其电感为L，单只自感抗Xk＝ωL，分裂电抗器的等值电路如题解图（a）所示。两个分支1、2的自感均为L，自感抗Xk＝ωL，互感耦合系数为K，则两个分支的互感为M＝KL，互感抗Xk＝ωLK＝0.5ωL＝Xk/2。
①正常运行时的等值电路如题解图（b）所示。功率方向从3至分支1、2，两个分支功率相等。正常运行时，当两分支正常负荷电流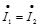
时，两分支线圈相互去磁使两分支线圈的磁通量减小一半，即感应电动势减小一半，使每分支等效电抗仅为自感抗的一半。分裂电抗器相当于一个电抗值为0.25Xk普通电抗器。
如题解图（c）所示，各分支等效电抗为：
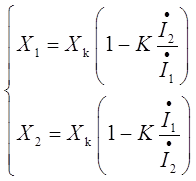
②当分支1出现短路时，由于I1≥I2，则X1≈Xk；当分支2出现短路时，由于I2≥I1，则X2≈Xk。分裂电抗器各分支的短路电抗等于正常运行电抗的2倍，解决了限制短路电流与限制正常电压降的矛盾。
因此，正常情况过渡到短路情况，电抗值增加4倍。
包含此试题的试卷
你可能感兴趣的试题
-
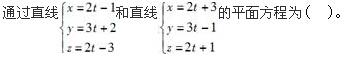
- A.x-z-2=0
- B.x+z=0
- C.x-2y+z=0
- D.x+y+z=1
- 查看答案
-
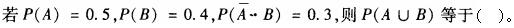
- A.0.6
- B.0.7
- C.0.8
- D.0.9
- 查看答案
微分方程y″+2y=0的通解是( )。
-
- A.y=Asin2x
- B.y=Acosx
- C.<img src='http://tp.mxqe.com/data/36/11311800_0.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- D.<img src='http://tp.mxqe.com/data/36/11311800_0_1.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- 查看答案
-
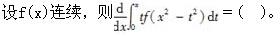
- A.<img src='http://tp.mxqe.com/data/36/11311799_0_1.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- B.<img src='http://tp.mxqe.com/data/36/11311799_0_2.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- C.<img src='http://tp.mxqe.com/data/36/11311799_0_3.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- D.<img src='http://tp.mxqe.com/data/36/11311799_0_4.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- 查看答案
-
- A.用洛必达法则后，求得极限为0
- B.<img src='http://tp.mxqe.com/data/36/11311798_0_1.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- C.<img src='http://tp.mxqe.com/data/36/11311798_0_2.jpg' alt='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学' title='电气工程师公共基础,章节练习,内部冲刺,第一部分工程科学基础,第一章高等数学'>
- D.因为不能用洛必达法则，故极限不存在
- 查看答案