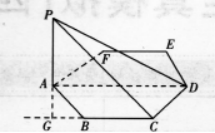
已知正六边形ABCDEF的边长为a，PA为过点A而垂直于正六边形所在平面M的垂线，且PA=a，求：
(I)点P到AB、BC、CD各边的距离；
(II)PD与平面M所成的角．
正确答案及解析
正确答案
解析
(I)如图所示，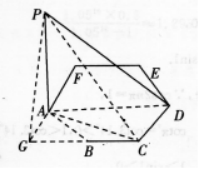
24题答案图
∵PA上平面M，∴PA上BC，
∴点P到AB的距离为a．过A作BC的垂线交CB的延长线于G，连结PG，
∴BC上平面APG，即PG⊥AB，
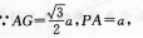
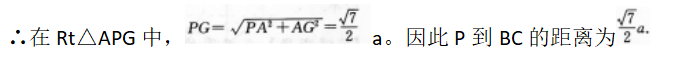
∵PA上平面M，
∴AC是PC在平面M上的射影，
又∵AD是正六边形ABCDEF外接圆的直径，
∴∠ACD=90o．
因此AC⊥CD，所以CD⊥平面ACP，即PC是P到CD的距离，
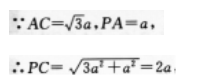
因此P到CD的距离为2a．
(Ⅱ)设PD与DA所夹的角为口，在Rt△PAD中，
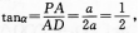
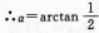(VI)为PD与平面M所夹的角．
