在三棱锥A-BCD中,AC⊥底面BCD,BD⊥DC,BD=DC,AC=a,∠ABC=30°,则点C到平面ABD的距离是( )
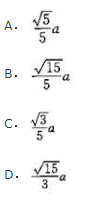
- A.见图A
- B.见图B
- C.见图C
- D.见图D
正确答案及解析
正确答案
B
解析
先证明BD⊥平面ACD,可得△ABD是直角三角形,分别计算△ABD和△BCD的面积,作等积变换VA-BCD=VC-ABD;可求得点C到平面ABD的距离.
在三棱锥A-BCD中,AC⊥底面BCD,BD⊥DC,BD=DC,AC=a,∠ABC=30°,则点C到平面ABD的距离是( )
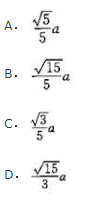
先证明BD⊥平面ACD,可得△ABD是直角三角形,分别计算△ABD和△BCD的面积,作等积变换VA-BCD=VC-ABD;可求得点C到平面ABD的距离.