已知离散型随机变量X的概率分布为
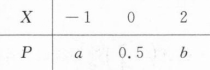
且E（X）=0．
（1）求a，b；
（2）求E[X（X+1）]．
正确答案及解析
正确答案
解析
（1）由概率的性质可知a+0．5+b=1，
又E（X）=0，得-1×a+0×0．5+2×b=0，
故有a=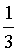
，b=
．
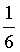（2）E[X（X+1）]=E（X2+X）=E（X2）+E（X），
而E（X2）=D（X）+[E（X）]2
=
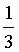·（-1-0）2+
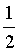·（0-0）2+
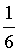·（2-0）2
=1。
因此E[X（X+1）]=1+0=1．
已知离散型随机变量X的概率分布为
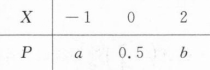
且E（X）=0．
（1）求a，b；
（2）求E[X（X+1）]．
（1）由概率的性质可知a+0．5+b=1，
又E（X）=0，得-1×a+0×0．5+2×b=0，
故有a=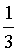，b=．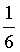
（2）E[X（X+1）]=E（X2+X）=E（X2）+E（X），
而E（X2）=D（X）+[E（X）]2
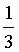=·（-1-0）2+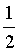·（0-0）2+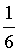·（2-0）2
=1。
因此E[X（X+1）]=1+0=1．