f(1)=1,f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出,n>1时,有向量的递推关系式:
(f(n+1),f(n))=(f(n),f(n-1))A
其中A是2*2矩阵( )。从而,(f(n+1),f(n)=(f(2),f(1))*( )
- A.An-1
- B.An
- C.An+1
- D.An+2
正确答案及解析
正确答案
A
解析
此题考查菲波那契(Fibonacci)数列及数学代数知识,根据矩阵乘法运算法则,有
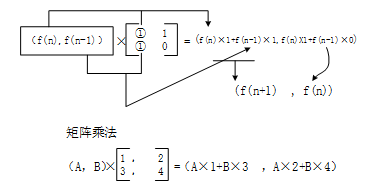
从运算规则中可以看出,矩阵A与数列项形成相差为1的关系,因此是n-1
包含此试题的试卷
你可能感兴趣的试题
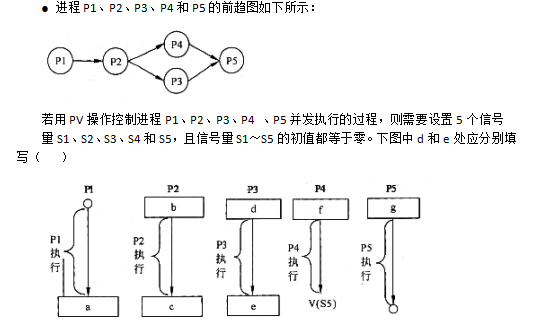
-
- A.V(S2)和P(S4)
- B.P(S2)和V(S4)
- C.P(S2)和P(S4)
- D.V(S2)和V(S4)
- 查看答案
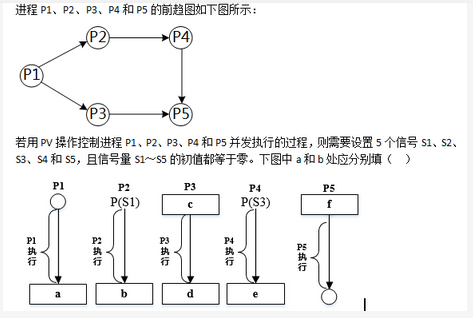
-
- A.V(S1)P(S2)和V(S3)
- B.P(S1)V(S2)和V(S3)
- C.V(S1)V(S2)和V(S3)
- D.P(S1)P(S2)和V(S3)
- 查看答案
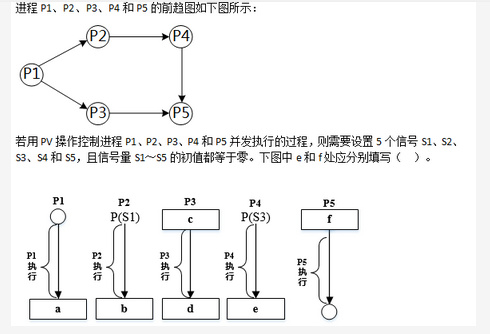
-
- A.P(S4)和V(S4)V(S5)
- B.V(S5)和P(S4)P(S5)
- C.V(S3)和V(S4)V(S5)
- D.P(S3)和P(S4)V(P5)
- 查看答案
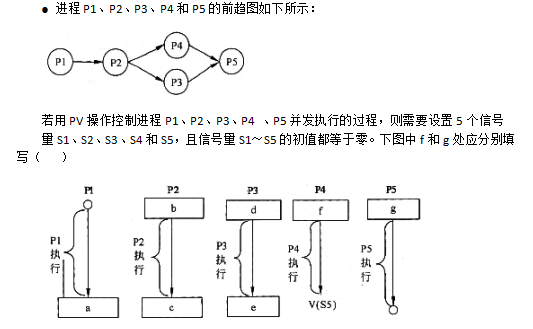
-
- A.P(S3)和V(S4)V(S5)
- B.V(S3)和P(S4)P(S5)
- C.P(S3)和P(S4)P(S5)
- D.V(S3)和V(S4)V(S5)
- 查看答案
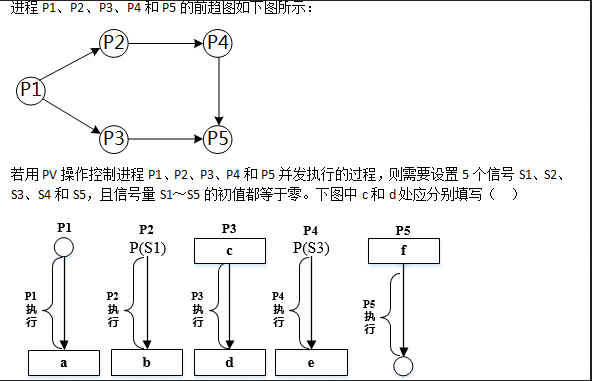
-
- A.P(S2)和P(S4)
- B.P(S2)和V(S4)
- C.V(S2)和P(S4)
- D.V(S2)和V(S4)
- 查看答案