阅读以下说明和代码，填补代码中的空缺，将解答填入答题纸的对应-名校题库网

题目详情

全站导航

首页试卷库试题库

试卷导航

学历类职业资格公务员医卫类建筑工程外语类计算机类财会类

试题导航

学历类职业资格公务员医卫类建筑工程外语类计算机类财会类

阅读以下说明和代码，填补代码中的空缺，将解答填入答题纸的对应栏内。

【说明】

下面的程序利用快速排序中划分的思想在整数序列中找出第k小的元素（即将元素从小到大排序后，取第k个元素）。

对一个整数序列进行快速排序的方法是：在待排序的整数序列中取第一个数作为基准值，然后根据基准值进行划分，从而将待排序的序列划分为不大于基准值者（称为左子序列）和大于基准值者（称为右子序列），然后再对左子序列和右子序列分别进行快速排序，最终得到非递减的有序序列。

例如，整数序列“19, 12, 30, 11,7,53, 78, 25"的第3小元素为12。整数序列“19,12,7,30,11,11,7,53,78,25,7"的第3小元素为7。

函数partition（int a[ ], int low,int high）以a[low]的值为基准，对a[low]、a[low+1]、…、

a[high]进行划分，最后将该基准值放入a[i] (low≤i≤high)，并使得a[low]、a[low+1]、，．．、

A[i-1]都小于或等于a[i]，而a[i+1]、a[i+2]、．．、a[high]都大于a[i]。

函数findkthElem(int a[],int startIdx,int endIdx,inr k)在a[startIdx]、a[startIdx+1]、...、a[endIdx]中找出第k小的元素。

#include ＜stdio.h>

#include ＜stdlib.h>

int partition(int a [ ],int low, int high)

{//对 a[low..high]进行划分,使得a[low..i]中的元素都不大于a[i+1..high]中的元素。

int pivot=a[low]; //pivot表示基准元素

int i=low,j=high;

while(( 1 ) ){

while(i＜j&&a[j]>pivot)--j;

a[i]=a[j];

while(i＜j&&a[i]＜=pivot)++i;

a[j]=a[i];

}

( 2 ) ; //基准元素定位

return i;

}

int findkthElem(int a[],int startIdx,int endIdx, int k)

{//整数序列存储在a[startldx..endldx]中,查找并返回第k小的元素。

if (startIdx＜0 ||endIdx＜0 || startIdx > endIdx || k＜1 ||k-1>endIdx ||k-1＜startIdx)

return-1; //参数错误

if(startIdx＜endIdx){

int loc=partition(a, startIdx, endIdx); //进行划分,确定基准元素的位置

if (loc== k-1) //找到第k小的元素

return ( 3 ) ;

if(k-1 ＜ loc) //继续在基准元素之前查找

return findkthElem(a , ( 4 ), k ) ;

else //继续在基准元素之后查找

return findkthElem(a, ( 5 ),k);

}

return a[startIdx];

}

int main()

{

int i, k;

int n;

int a[] = {19, 12, 7, 30, 11, 11, 7, 53, 78, 25, 7};

n= sizeof(a)/sizeof(int); //计算序列中的元素个数

for (k=1;k＜n+1;k++){

for(i=0;i＜n;i++){

printf("%d\t",a[i]);

}

printf("\n");

printf("elem %d=%d\n",k,findkthElem(a,0,n-1,k));//输出序列中第k小的元素

}

return 0;

}

正确答案及解析

正确答案

解析

1、i!=j或者i＜j

2、a[i]=pivot

3、a[loc]

4、startIdx,loc-1

5、loc+1,endIdx

此题考查排序算法的应用，快速排序的思想是：通过一趟排序将待排序的记录划分为独立的两部分，其中一部分记录的关键字均比另一部分记录的关键字小，然后利用递归再分别对这两部分记录继续进行排序，以达到整个序列有序。一趟排序的具体做法是：设两个变量low和high，初值分别指向序列的第一个和最后一个，通常将第一个记录的关键字设为pivotkey，首先从high所指位置向前搜索，找到第一个关键字小于pivotkey的记录并互相交换，然后从low位置向后搜索，找到第一个大于pivotkey的记录并互相交换，重复这两步直到low=high为止。

本题是要找出第K个元素，要求将元素从小到大排序，然后取第K个元素。如数组中的元素是19,12,7,30,11,11,7,53,78,25,7，则第1，2，3个元素都是7，第4，5个元素是11，第6个元素是12，第11个元素是78，本题就是要找出前K个元素中第K个元素，K是不断变化的，K的取值范围是从1到数组长度，第K个元素也是不断变化的。

Partition函数是找到基准元素的位置，根据快速排序算法，循环判断的条件是最小值和最大值不相等，即1处应该填i!=j或者i＜j，当开始位置和结束位置不相等时则从数组的两端分别向中间扫描。扫描的方法是：依次比较数组的high与基准pivot的大小，如果a[j]>=pivot，则j--，直到遇到第一个pivot>a[j]，则停止移动，将a[j]赋值给a[i]，同时依次比较数据的low与基准pivot的大小，如果a[i]＜=pivot，则i++，直到遇到第一个pivot＜a[i]，则停止移动，将a[i]赋值给a[j]，直到i等于j，则完成一次快速排序，此时找到了基准元素的位置，将基准元素移到正确的位置，赋给a[i]，并返回i的值，作为函数partition的结果。

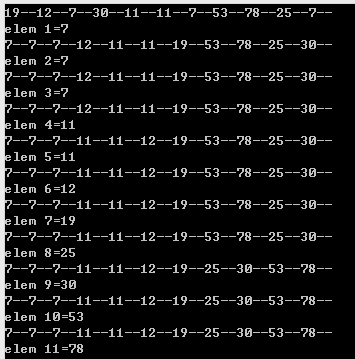
FindthElem函数是查找并返回第k小的元素，它实际上是将原来应该在快速排序中递归完成的功能换成了FindthElem函数去完成，形参k用来接收partition函数中的i，第3处上面的if(loc==k-1)判断成立的时候表明此时找到了第k个的元素，所以直接返回数组第loc位置的元素，所以3处填a[loc]，第4处，第5处是当没有确定基准元素位置时，重复调用自己，重复调用时要判断k与loc的大小，小于loc时，表明要向前移动，大于loc时，要向后移动，所以处4处填startIdx,loc-1，第5处填loc+1,endIdx。答案是：1）i!=j或者i＜j 2）a[i]=pivot 3）a[loc] 4）startIdx,loc-1 5）loc+1,endIdx，整个程序运行结果是：

初级程序员,章节练习,基础复习,案例分析