0-1背包问题定义为:给定i个物品的价值v[1…i]、小重量w[1…i]和背包容量T,每个物品装到背包里或者不装到背包里。求最优的装包方案,使得所得到的价值最大。
0-1背包问题具有最优子结构性质。定义c[i][T]为最优装包方案所获得的最大价值,则可得到如下所示的递归式。
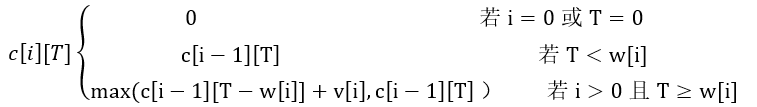
【c代码】
下面是算法的C语言实现。
(1)常量和变量说明
T:背包容量
v[]:价值数组
w[]:重量数组
c[][]:c[i][j]表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值
(2)C程序


【问题1】(8分)
根据说明和C代码,填充C代码中的空(1)-(4)。
【问题2】(4分)
根据说明和C代码,算法采用了(5)设计策略。在求解过程中,采用了(6)
(自底向上或者自顶向下)的方式。
【问题3】(3分)
若5项物品的价值数组和重量数组分别为v[]={0,1,6,18,22,28}和w[]={0,1,2,5,6,7}背包容量为T=11,则获得的最大价值为(7)。
正确答案及解析
正确答案
解析
【问题1】
(1)c[i][j]
(2)i>0&&j>=w[i]
(3)Calculate_Max_Value(v,w,i-1,j-w[i])+v[i]
(4)c[i][j]=temp
【问题2】
(5)动态规划
(6)自顶向下
【问题3】
(7)40
本题考查的是动态规划法,将中间结果存在二维数组c[][]当中。
【问题1】
结合题干描述中的递归式,函数最终返回值应该是c[i][T],又根据代码上下文,T在函数中传参为j,所以第(1)空返回的结果为c[i][j]。
根据递归式和代码上下文可知,c[i][j]=0已处理,if后面处理的是max递归部分,又根据上下文可以看到temp会与c[i][j]进行比较,递归时i=i-1,所以这里判断的是temp与c[i-1][T]的值,第(3)空的处理是将c[i-1][j-w[i]]+v[i]传递给temp,即temp=Calculate_Max_Value(v,w,i-1,j-w[i])+v[i],注意这里不是直接穿c[][]数组值,而是递归调用Calculate_Max_Value()函数。那么第(2)空缺失的判断条件根据第3个表达式条件为i>0且T>=w[i],对应代码中的参数即i>0&&j>=w[i]。
第(4)空是c[i][j]<temp比较后的返回值,根据题干,我们需要返回max最大值,最终返回的结果是c[i][j],因此要保证c[i][j]最大,当c[i][j]<temp时,将temp赋值给c[i][j],即c[i][j]=temp。
【问题2】
本题采用递归形式,并且求取的是全局最优解,中间结果存在二维数组c[][]当中,所以采用的是动态规划法。动态规划法采用递归形式,i会从N-1递减至0,所以是自顶向下的方式。
【问题3】
本题考查最优解,可以忽略题干描述,直接凑数,可得第3和第4个物品,重量为11,价值为40,此时为最优解,即为最大价值。
包含此试题的试卷
你可能感兴趣的试题
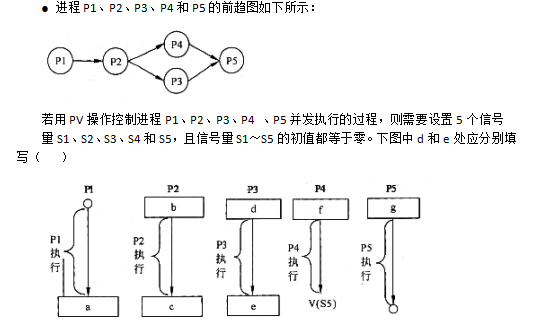
-
- A.V(S2)和P(S4)
- B.P(S2)和V(S4)
- C.P(S2)和P(S4)
- D.V(S2)和V(S4)
- 查看答案
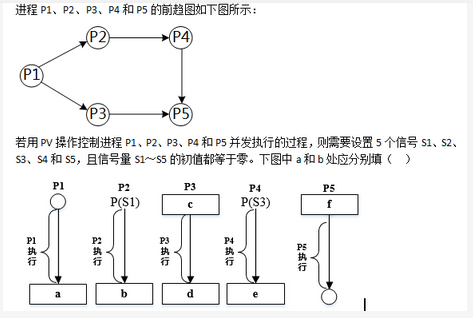
-
- A.V(S1)P(S2)和V(S3)
- B.P(S1)V(S2)和V(S3)
- C.V(S1)V(S2)和V(S3)
- D.P(S1)P(S2)和V(S3)
- 查看答案
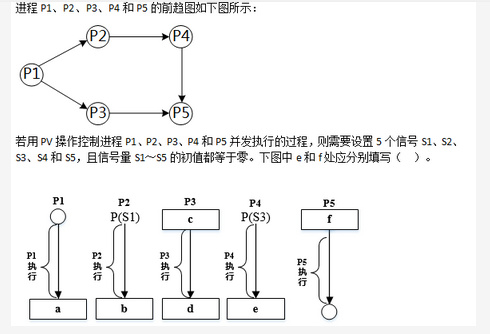
-
- A.P(S4)和V(S4)V(S5)
- B.V(S5)和P(S4)P(S5)
- C.V(S3)和V(S4)V(S5)
- D.P(S3)和P(S4)V(P5)
- 查看答案
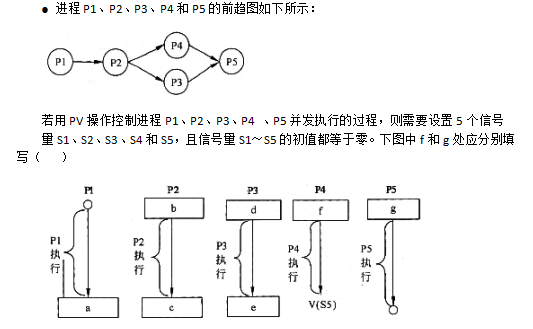
-
- A.P(S3)和V(S4)V(S5)
- B.V(S3)和P(S4)P(S5)
- C.P(S3)和P(S4)P(S5)
- D.V(S3)和V(S4)V(S5)
- 查看答案
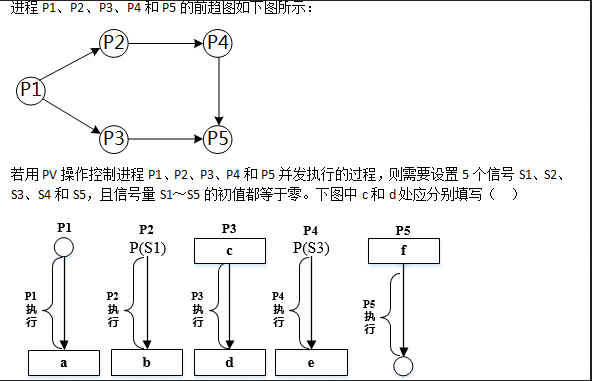
-
- A.P(S2)和P(S4)
- B.P(S2)和V(S4)
- C.V(S2)和P(S4)
- D.V(S2)和V(S4)
- 查看答案