试卷详情
全站导航
首页 试卷 试题 资讯
试卷导航
建筑工程 职业资格 公务员 财会类 医卫类 外语类 计算机类 学历类
试题导航
建筑工程 职业资格 公务员 财会类 医卫类 外语类 计算机类 学历类

2021年程序员模拟题4

开始做题

试卷预览

问答题

阅读以下C++代码，填充（1）~（5）的空缺，将解答填入答题纸的对应栏内。【说明】在下面程序横线处填上适当的字句，使其输出结果为：x=5x=6y=7x=8z=9【程序】#include＜iostream.h＞class X1{int x;（1）:X1(int xx=0){x=xx;}（2）void Output()(cout＜＜"x="＜＜x＜＜end;}};（3）Y1:public X1{int y;public:Y1(int xx=0,int yy=0):X1(xx){y=yy;}（2）void Output(){（4）Output();cout＜＜"y="＜＜y＜＜end1;}};class Z1:pubtic X1{int z:（5）:Z1(int xx=0,int zz=0):X1(xx){z=zz;}②void Output(){X1::Output();cout＜＜"z="＜＜z＜＜end1;}};void main(){X1 a(5);Y1 b(6,7);Z1 c(8,9);X1*p[3]={&a,&b,&c};For(int i=0;i＜3;i++){p[i]--＞Output();cout＜＜end1;}}

查看答案开始考试

正确答案：

本题解析：

（1）public

（2）virtual

（3）class

（4）X1::

（5）public

【解析】

通过对比三个类的定义就可以发现，在类X1和Z1的定义中缺少类的成员属性声明，而类一般将成员变量声明为公有的、私有的或受保护的三种类型中的一种，在类的定义中，我们一般将类的构造函数放在公有的属性下面，在题目中只能选择公有的属性了，因此，第1空和第5空中应该填“public”。对三个类的定义进行仔细观察后，我们同样可以发现，每个类中都定义了一个同名函数Output()，而且在后两个类的函数体中调用了函数Output()，由此，我们应该想到虚函数。虚函数的作用是允许在派生类中重新定义与基类同名的函数，并且可以通过基类指针或引用来访问基类和派生类中的同名函数。因此，第2空应该填“virtual”。第3空就简单了，考查类的定义，应该填类的标识符“class”。从程序中我们可以看到，类Y1和Z1都以公有的方式继承类X1。从输出的结果来分析，类Y1和Z1都输出了两个数，但单从类Z1的函数来看，只能输出一个变量的值z，因此，可以发现在类Z1中应该和类Y1一样，都调用了类X1的函数Output()，因此，第4空的答案为“X1::”。

问答题

阅读以下说明和流程图，填写流程图中的空缺，将解答填入答题纸的对应栏内。【说明】如果一个自然数N恰好等于它所有不同的真因子（即N的约数以及1，但不包括N）之和S，则称该数为“完美数”。例如6＝1＋2＋3，28＝1＋2＋4＋7＋14，所以6和28都是完美数。显然，6是第1个（即最小的）完美数。下面流程图的功能是求500以内所有的完美数。【流程图】

初级程序员,模拟考试,2021年程序员模拟题4

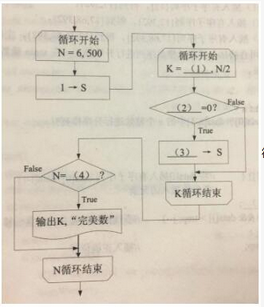
循环开始框中要注明：循环变量＝初始值，终值［，步长］，步长为1时可以缺省。如果某自然数小于其所有真因子之和（例如24＜1＋2＋3＋4＋6＋8＋12），则称该自然数为亏数；如果某自然数大于其所有真因子之和（例如8＞1＋2＋4），则称该自然数为贏数；如果某自然数等于从1开始的若干个连续自然数之和（例如10＝1＋2＋3＋4）则称该自然数为三角形数。据此定义，自然数496是（ ）。供选择答案：A.亏数 B.赢数 C.完美数，非三角形数 D.完美数和三角形数

查看答案开始考试

正确答案：

本题解析：

（1）2（2）N%K（3）S+K（4）S（5）D

【解析】

流程图的功能是求500以内所有的完美数，N的值范围是6~500，因此N是需要判断是否为完美数，首先需要求出N的所有真因子，然后再判断N和真因子之和是否相等，从流程图可以看出S是保存真因子和的变量，K是保存真因子的变量，因此K的初始值是2，终值是N/2，因此第（1）空处填写：2；判断K是否为N的真因子，即判断N%K（N除以K取余）是否为0，第（2）空填写：N%K；当K为N的真因子时，需要计算所有K的和，即S=S+K，第（3）空填写：S+K；最后判断N和S是否相等，第（4）空填写：S。496的真因子有：1、2、4、8、16、31、62、124、248，1+2+4+8+16+31+62+124+248=496；因此496是完美数，同时496=（1+2+3+4+……+30+31），因此496是完美数和三角形数。

问答题

阅读以下说明和C代码，填写程序中的空（1）~（5），将解答写入答题纸的对应栏内。【说明】直接插入排序是一种简单的排序方法，具体做法是：在插入第i个关键码时，k1，k2，…，ki-1已经排好序，这时将关键码ki依次与关键码ki-1，ki-2，…，进行比较，找到ki应该插入的位置时停下来，将插入位置及其后的关键码依次向后移动，然后插入ki。例如，对｛17，392，68，36｝按升序作直接插入排序时，过程如下：第1次：将392（i＝1）插入有序子序列{17}，得到{17，392}；第2次：将68（i＝2）插入有序子序列{17，392}，得到{17，68，392}；第3次：将36（i＝3）插入有序子序列{17，68，392}，得到{17，36，68，392}，完成排序。下面函数 insertSort用直接插入排序对整数序列进行升序排列，在main函数中调用insertSort并输出排序结果。 【C代码】void insert Sort(int data[],int n)/*用直接插入排序法将data[0]～ data[n-1]中的n个整数进行升序排列*/{ int i,j; int tmp; for(i=1; i＜n;i++){ if(data[i]＜data[i-1])｛ //将data[i]插入有序子序列data[0]～data[i-1] tmp=data[i]; //备份待插入的元素 data[i]=（1）; for(j=i-2;j>=0 && data[j] > tmp;j----) //查找插入位置并将元素后移 （2）; （3） =tmp; //插入正确位置 }/*if*/ }/*for*/}/*insertSort*/ int main(){ int *bp,*ep; int n,arr[]={17,392,68,36,291,776,843,255}; n = sizeof(arr) / sizeof(int); insertSort(arr,n); bp= （4） ; ep = arr+n; for( ;bp＜ep; bp++) //按升序输出数组元素 printf("%d\t", （5） ); return 0;阅读以下说明和C代码，填写程序中的空（1）~（5），将解答写入答题纸的对应栏内。【说明】直接插入排序是一种简单的排序方法，具体做法是：在插入第i个关键码时，k1，k2，…，ki-1已经排好序，这时将关键码ki依次与关键码ki-1，ki-2，…，进行比较，找到ki应该插入的位置时停下来，将插入位置及其后的关键码依次向后移动，然后插入ki。例如，对｛17，392，68，36｝按升序作直接插入排序时，过程如下：第1次：将392（i＝1）插入有序子序列{17}，得到{17，392}；第2次：将68（i＝2）插入有序子序列{17，392}，得到{17，68，392}；第3次：将36（i＝3）插入有序子序列{17，68，392}，得到{17，36，68，392}，完成排序。下面函数 insertSort用直接插入排序对整数序列进行升序排列，在main函数中调用insertSort并输出排序结果。 【C代码】void insert Sort(int data[],int n)/*用直接插入排序法将data[0]～ data[n-1]中的n个整数进行升序排列*/{ int i,j; int tmp; for(i=1; i＜n;i++){ if(data[i]＜data[i-1])｛ //将data[i]插入有序子序列data[0]～data[i-1] tmp=data[i]; //备份待插入的元素 data[i]=（1）; for(j=i-2;j>=0 && data[j] > tmp;j----) //查找插入位置并将元素后移 （2）; （3） =tmp; //插入正确位置 }/*if*/ }/*for*/}/*insertSort*/ int main(){ int *bp,*ep; int n,arr[]={17,392,68,36,291,776,843,255}; n = sizeof(arr) / sizeof(int); insertSort(arr,n); bp= （4） ; ep = arr+n; for( ;bp＜ep; bp++) //按升序输出数组元素 printf("%d\t", （5） ); return 0;}

查看答案开始考试

正确答案：

本题解析：

（1）data[i-1]（2）data[j+1]=data[j]（3）data[j+1]（4）arr（5）*bp

【解析】

直接插入排序法是将关键码插入已经排好的序列中，因此将data[i]插入序列data[0]~data[i-1]中，此时序列data[0]~data[i-1]已经按照升序排列好，而data[i]应插入位置前的数据应该比data[i]小，而插入位置后的数据应比data[i]大，在if语句中判断data[i]＜data[i-1]中可以看出，在进行插入运算时，是从序列data[0]~data[i-1]最后一个数据data[i-1]向前逐一进行比较，若data[i]>=data[i-1]，则将data[i]插入到d[i-1]后；若data[i]＜data[i-1]，data[i]需要与data[i-2]进行比较，如此依次进行，此时需要将data[i]备份并将data[i-1]后移，即temp=data[i]； data[i]=data[i-1]；之后是进行比较，即for(j=i-2;j>=0&&data[j]>tmp;j--)循环，从data[i-2]开始向前逐一比较，即j从i-2开始向0循环，若data[j]>tmp，则进行for循环，此时需要将data[j]即data[i-2]的值后移，使得data[i-1]=data[i-2]，即data[j+1]=data[j]，然后j--，用tmp与data[j]进行比较，如果tmp＜ data[j]，则说明tmp应放在data[j]之前，那么data[j]需要继续往后移动。所以data[j+1]= data[j]。 当该循环结束时，此时有2种情况：（1）j=-1＜0，此时data[0]>tmp；应使得data[0]后移，即data[1]=data[0]，data[0]=tmp，因此第3空填写data[j+1]；（2）data[j]＜=tmp；此时需要将tmp插入到data[j]后，即data[j+1]=tmp。 在main函数中调用insertSort函数并输出数组元素，在for(; bp＜ep;bp++)中循环变量是bp，因此输出的是bp指向的数组元素，即调用insertSort函数后返回的数组arr，因此bp=arr（bp是指针变量，数组名arr可以直接将数组地址传递给bp）；在printf函数中输出bp；因此printf(“%d\n”，*bp)。

问答题

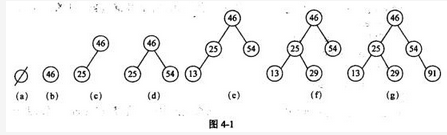
阅读以下说明和C代码，填补代码中的空缺，将解答填入答题纸的对应栏内。【说明】二叉查找树又称为二叉排序树，它或者是一棵空树，或者是具有如下性质的二叉树。（1）若它的左子树非空，则左子树上所有结点的值均小于根结点的值。（2）若它的右子树非空，则右子树上所有结点的值均大于根结点的值。（3）左、右子树本身就是两棵二叉查找树。二叉查找树是通过依次输入数据元素并把它们插入到二叉树的适当位置上构造起来的，具体的过程是：每读入一个元素，建立一个新结点，若二叉查找树非空，则将新结点的值与根结点的值相比较，如果小于根结点的值，则插入到左子树中，否则插入到右子树中；若二叉查找树为空，则新结点作为二叉查找树的根结点。根据关键码序列{46，25，54，13，29，91}构造一个二叉查找树的过程如图4-1所示。

初级程序员,模拟考试,2021年程序员模拟题4

设二叉查找树采用二叉链表存储，结点类型定义如下：

typedef int KeyType；typedef struct BSTNode{KeyType key；struct BSTNode *left,*right；}BSTNode,*BSTree；

图4-1(g)所示二叉查找树的二叉链表表示如图4-2所示。

初级程序员,模拟考试,2021年程序员模拟题4

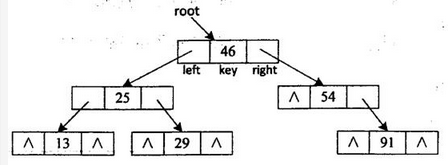
函数int InsertBST(BSTree *rootptr,KeyType kword)功能是将关键码kword插入到由rootptr指示出根结点的二叉查找树中，若插入成功，函数返回1，否则返回0。【C代码】

int lnsertBST(BSTree*rootptr，KeyType kword)/*在二叉查找树中插入一个键值为kword的结点，若插入成功返回1，否则返回0；*rootptr为二叉查找树根结点的指针*/{BSTree p,father;(1) /*将father初始化为空指针*/p=*rootptr; /*p指示二叉查找树的根节点*/while(p&&（2）){ /*在二叉查找树中查找键值kword的结点*/father=p;if(kword＜p-＞key)p=p-＞left；elsep=p-＞right；}if((3))return 0; /*二叉查找树中已包含键值kword，插入失败*/ p=(BSTree)malloc((4)); /*创建新结点用来保存键值kword*/If(!p)return 0; /*创建新结点失败*/p-＞key=kword；p-＞left=NULL；p-＞right=NULL； If(!father)(5) =p； /*二叉查找树为空树时新结点作为树根插入*/elseif(kword＜father-＞key)(6)；/*作为左孩子结点插入*/else(7)；/*作右孩子结点插入*/return 1；}/*InsertBST*/

查看答案开始考试

正确答案：

本题解析：

father=(void*)0keyword!=p-keypsizeof(BSTNode)*rootptrfather-left=pfather-right=p

问答题

阅读下列说明和C代码，回答问题1至问题3，将解答写在答题纸的对应栏内。【说明】假币问题：有n枚硬币，其中有一枚是假币，已知假币的重量较轻。现只有一个天平，要求用尽量少的比较次数找出这枚假币。【分析问题】将n枚硬币分成相等的两部分：（1）当n为偶数时，将前后两部分，即1…n/2和n/2+1…0，放在天平的两端，较轻的一端里有假币，继续在较轻的这部分硬币中用同样的方法找出假币：（2）当n为奇数时，将前后两部分，即1…(n -1)/2和(n+1)/2+1…0，放在天平的两端，较轻的一端里有假币，继续在较轻的这部分硬币中用同样的方法找出假币；若两端重量相等，则中间的硬币，即第 (n+1)/2枚硬币是假币。【C代码】下面是算法的C语言实现，其中：

coins[]： 硬币数组first，last：当前考虑的硬币数组中的第一个和最后一个下标

#include ＜stdio.h>

int getCounterfeitCoin(int coins[]， int first，int last){int firstSum = 0，lastSum = 0;int ì;If(first==last-1){ /*只剩两枚硬币*/if(coins[first] ＜ coins[last])return first;return last;}

if((last - first + 1) % 2 ==0){ /*偶数枚硬币*/for(i = first;i ＜( 1 );i++){firstSum+= coins[i];}for(i=first + (last-first) / 2 + 1;i ＜ last +1;i++){lastSum += coins[i];}if( 2 ){Return getCounterfeitCoin(coins,first,first+(last-first)/2;)}else{Return getCounterfeitCoin(coins,first+(last-first)/2+1,last;)}}else{ /*奇数枚硬币*/For(i=first;i＜first+(last-first)/2;i++){firstSum+=coins[i];}For(i=first+(last-first)/2+1;i＜last+1;i++){lastSum+=coins[i];}If(firstSum＜lastSum){return getCounterfeitCoin(coins,first,first+(last-first)/2-1);}else if(firstSum>lastSum){return getCounterfeitCoin(coins,first+(last-first)/2-1,last);}else{Return( 3 )}}}

【问题一】（6分）根据题干说明，填充C代码中的空（1）-（3）【问题二】（4分）根据题干说明和C代码，算法采用了（ ）设计策略。函数getCounterfeitCoin的时间复杂度为（ ）（用O表示）。【问题三】（5分）若输入的硬币数为30，则最少的比较次数为（ ），最多的比较次数为（ ）。

查看答案开始考试

正确答案：

本题解析：

【问题一】答案：（1）first+(last-first)/2 +1或(first+last)/2+1 （2）firstSum＜lastSum（3）first+(last-first)/2 或(first+last)/2【问题二】答案：分治法、O（nlogn）【问题三】答案：2、4

问答题

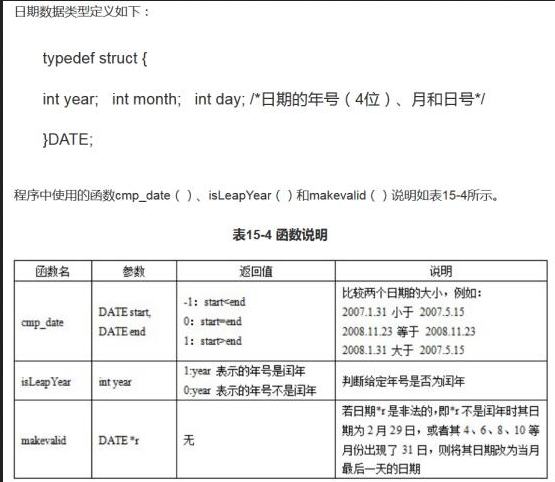
阅读以下问题说明、C 程序和函数，将解答填入答题纸的对应栏内。

[说明]

函数count_ months ( DATE start, DATE end )的功能是:计算两个给定日期之间所包含的完整月份数。

该函数先算出起止日期中所含的完整年数,再计算余下的完整月份数。规定两个相邻年份的同月同日之间的问隔为1年。例如, 2007.5.30~2008.5.30的间隔为1年。若相邻两年中前一年是闰年,并且日期是2月29日,则到下一年的2月28日为1年,即2008. 229-2009 228的间隔为1年。

规定两个相邻月份的相同日之间的间隔为1个月,但需要特别考虑月末的特殊情况。例如，2007.1.29-2007.2.28的间隔为1个月,同理, 2007.1.30、2007 2.28、2007.1.31-2007.2 28的间隔都是1个月。

计算起止日期间隔不足一年的完整月份数时 ,分如下两种情况:

1)起止日期不跨年度。先用终止日期的月号减去起始日期的月号得到月份数,然后再根据情况进行修正。例如，起止日期为2008.3.31~2008.9.20.通过月号算出月份数为6.修正时。通过调用函数makevalid将2008.9.31改为2008 9.30,与终止日期2008.9 20比较后,将月份数修正为5.

2)起止日期跨年度。计算方法如下例所示:对于起止日期2008.7.25~2009.3.31,先计算2008.7 25~2008.12.25

的月份数为5.再算出2008.12 25~2009.3.25的月份数为3.因此2008.7 .25~2009.3.31之间的完整月份数为8.

初级程序员,模拟考试,2021年程序员模拟题4

初级程序员,模拟考试,2021年程序员模拟题4

初级程序员,模拟考试,2021年程序员模拟题4

初级程序员,模拟考试,2021年程序员模拟题4

查看答案开始考试

正确答案：

本题解析：

初级程序员,模拟考试,2021年程序员模拟题4

初级程序员,模拟考试,2021年程序员模拟题4

初级程序员,模拟考试,2021年程序员模拟题4

问答题

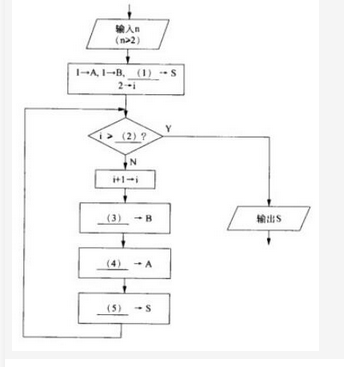
阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】

初级程序员,模拟考试,2021年程序员模拟题1

查看答案开始考试

正确答案：

本题解析：

（1）2或A+B（2）n（3）A+B（4）B-A（5）S+B

【解析】

菲波那契数列的特点是首2项都是1，从第3项开始，每一项都是前两项之和。该数列的前几项为1，1，2, 3，5，8，…。在流程图中，送初始值1—A，2—B后，显然前2项的和S应等于2,所以（1）处应填2 (或A+B)。此时2→i (i表示动态的项编号），说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和，循环可以结束了。因此（2）处填n。判断框中用“>”或“≥”的效果是一样的，因为随着i的逐步增1，只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些，以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1，继续往下计算。原来的前两项值（分别在变量A和B中）将变更成新的前两项再放到变量A和B中。

初级程序员,模拟考试,2021年程序员模拟题4

首先可以用A+B—B实现（原A) + (原B)—(新B)，因此（3）处填A+B。为了填新A值（原来的B值)，不能用B—A，因为变量B的内容已经改变为（原A) + (原B)，而B-A正是（（原A) + (原B))-(原A)=(原B)，因此可以用B-A—A来实现新A的赋值。这样，（4）处填B-A。最后应是前n项和值的累加（比原来的S值增加了新B值)，所以（5）处应填S+B。填完各个空后，最好再用具体的数值来模拟流程图走几个循环检查所填的结果（这是防止逻辑上出错的好办法）。

其他考生还关注了更多 +